Les axiomes de probabilité ce sont des propositions mathématiques faisant référence à la théorie des probabilités, qui ne méritent pas de preuve. Les axiomes ont été établis en 1933 par le mathématicien russe Andrei Kolmogorov (1903-1987) dans son travail Fondamentaux de la théorie des probabilités et jeté les bases de l'étude mathématique des probabilités.
Lors de la réalisation d'une certaine expérience aléatoire ξ, l'espace échantillon E est l'ensemble de tous les résultats possibles de l'expérience, également appelé événements. Tout événement est noté A et P (A) est la probabilité de son occurrence. Puis Kolmogorov a établi que:
-Axiome 1 (pas la négativité): la probabilité qu'un événement A se produise est toujours positive ou nulle, P (A) ≥0. Lorsque la probabilité d'un événement est de 0, il est appelé événement impossible.
-Axiome 2 (certitude): chaque fois qu'un événement appartient à E, sa probabilité d'occurrence est de 1, que nous pouvons exprimer comme P (E) = 1. C'est ce qu'on appelle un événement sûr, car lors de la conduite d'une expérience, avec toute certitude, il y a un résultat.
-Axiome 3 (ajout): dans le cas de deux ou plusieurs événements incompatibles deux par deux, appelés A1, Àdeux, À3…, La probabilité que l'événement A se produise1 plus le Adeux plus le A3 et ainsi de suite, c'est la somme des probabilités que chacune se passe séparément.
Ceci est exprimé comme: P (A1 U Adeux U A3 U…) = P (A1) + P (Adeux) + P (A3) + ...
Index des articles
Les axiomes de probabilité sont largement utilisés dans une multitude d'applications. Par exemple:
Une punaise ou une punaise est lancée en l'air, et lorsqu'elle tombe au sol, il est possible d'atterrir avec la pointe vers le haut (U) ou avec la pointe vers le bas (D) (nous n'envisagerons pas d'autres possibilités). L'espace échantillon de cette expérience se compose de ces événements, alors E = U, D.
En appliquant les axiomes, nous avons:
P (E) = 1 (Axiome 2)
Mais P (E) = P (U) + P (D) (Axiome 3), car ces événements sont incompatibles entre eux ou disjoints. La punaise ne tombe pas avec la pointe vers le haut ou vers le bas en même temps, c'est l'un ou l'autre, mais pas les deux, car d'autres possibilités ne sont pas envisagées. Ensuite:
P (U) + P (D) = 1
P (U) = 1 - P (D)
S'il est tout aussi probable qu'il atterrisse vers le haut ou vers le bas, P (U) = P (D) = ½ (Axiome 1). Cependant, il se peut que la construction et la conception de la punaise soient plus susceptibles de tomber d'une manière ou d'une autre. Par exemple, il se peut que P (U) = ¾ tandis que P (D) = ¼ (Axiome 1).
Notez que dans les deux cas, la somme des probabilités donne 1. Cependant, les axiomes n'indiquent pas comment attribuer les probabilités, du moins pas complètement. Mais ils affirment qu'il s'agit de nombres compris entre 0 et 1 et que, comme dans ce cas, la somme de tous est 1.
Les axiomes de probabilité ne sont pas une méthode d'attribution de la valeur de probabilité. Pour cela, il existe trois options compatibles avec les axiomes:
Chaque événement se voit attribuer la même probabilité de se produire, puis la probabilité d'occurrence est définie comme suit:
P (A) = nombre de cas favorables à l'événement A / nombre de cas possibles
Par exemple, quelle est la probabilité de tirer un as d'un jeu de cartes françaises? Le jeu a 52 cartes, 13 de chaque couleur et il y a 4 couleurs. Chaque couleur a 1 as, donc au total il y a 4 as:
P (comme) = 4/52 = 1/13
La règle de Laplace est limitée aux espaces d'échantillons finis, où chaque événement est également probable.
Ici, l'expérience doit être répétable, car la méthode est basée sur la réalisation d'un grand nombre de répétitions..
Faisons i répétitions de l'expérience ξ, dont nous trouvons que n est le nombre de fois qu'un certain événement A se produit, alors la probabilité que cet événement se produise est:
P (A) = limje → ∞ (ni)
Où n / i est la fréquence relative d'un événement.
Définir P (A) de cette manière satisfait les axiomes de Kolmogorov, mais présente l'inconvénient que de nombreux tests doivent être effectués pour que la probabilité soit appropriée.
Une personne ou un groupe de personnes peut convenir d'attribuer la probabilité à un événement, par son propre jugement. Cette méthode présente l'inconvénient que différentes personnes peuvent attribuer différentes probabilités au même événement..
Dans l'expérience de lancer simultanément 3 pièces honnêtes, obtenez les probabilités des événements décrits:
a) 2 têtes et une queue.
b) 1 tête et deux queues
c) 3 croix.
d) Au moins 1 visage.
Les têtes sont désignées par C et les queues par X. Mais il existe plusieurs façons d'obtenir deux têtes et une queue. Par exemple, les deux premières pièces peuvent atterrir des têtes et la troisième peut atterrir des queues. Ou le premier peut tomber des têtes, les deuxièmes queues et les troisièmes têtes. Et enfin le premier peut être des queues et les têtes restantes.
Pour répondre aux questions, il est nécessaire de connaître toutes les possibilités, qui sont décrites dans un outil appelé diagramme arborescent ou alors arbre des probabilités:
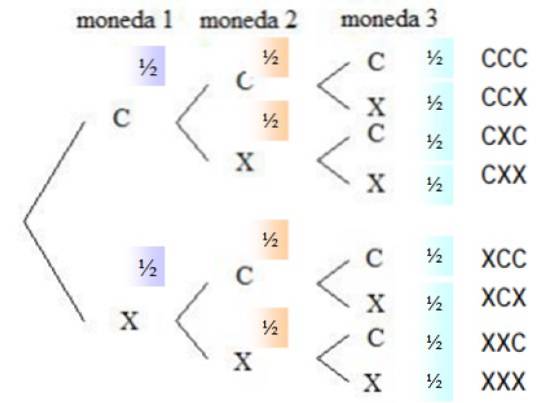
La probabilité qu'une pièce de monnaie sorte des têtes est de 1/2, il en va de même pour les queues, puisque la pièce est honnête. Dans la colonne de droite sont répertoriées toutes les possibilités offertes par le tirage au sort, c'est-à-dire l'espace échantillon.
A partir de l'espace échantillon, les combinaisons qui répondent à l'événement demandé sont choisies, car l'ordre dans lequel les faces apparaissent n'est pas important. Il y a trois événements favorables: CCX, CXC et XCC. La probabilité que chaque événement se produise est:
P (CCX) = ½. ½. ½ = 1/8
La même chose se produit pour les événements CXC et XCC, chacun a une probabilité de 1/8 de se produire. Par conséquent, la probabilité d'obtenir exactement 2 têtes est la somme des probabilités de tous les événements favorables:
P (recto-verso) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
Trouver la probabilité qu'exactement deux croisements se produisent est un problème analogue au précédent, il y a aussi trois événements favorables pris dans l'espace d'échantillonnage: CXX, XCX et XXC. Donc:
P (2 croix) = 3/8 = 0,375
Intuitivement, nous savons que la probabilité d'obtenir 3 queues (ou 3 têtes) est plus faible. Dans ce cas, l'événement recherché est XXX, en fin de colonne de droite, dont la probabilité est:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Il est demandé d'obtenir au moins 1 face, cela signifie que 3 faces, 2 faces ou 1 face peuvent sortir. Le seul événement incompatible avec cela est celui dans lequel 3 queues sortent, dont la probabilité est de 0,125. La probabilité recherchée est donc:
P (au moins 1 tête) = 1 - 0,125 = 0,875.
Personne n'a encore commenté ce post.