Chocs élastiques en une dimension, cas particuliers, exercices

Les chocs élastiques ou les collisions élastiques consistent en des interactions brèves mais intenses entre les objets, dans lesquelles à la fois la quantité de mouvement et l'énergie cinétique sont conservées. Les crashs sont des événements très fréquents dans la nature: des particules subatomiques aux galaxies, en passant par les boules de billard et les autos tamponneuses dans les parcs d'attractions, ce sont tous des objets capables d'entrer en collision.

Lors d'une collision ou d'une collision, les forces d'interaction entre les objets sont très fortes, bien plus que celles qui peuvent agir de l'extérieur. De cette façon, on peut affirmer que lors de la collision, les particules forment un système isolé.

Dans ce cas, il est vrai que:

P_{ou alors} = P_F

La quantité de mouvement P_{ou alors} avant la collision est la même qu'après la collision. Cela est vrai pour tout type de collision, à la fois élastique et inélastique..

Considérez maintenant ce qui suit: lors d'une collision, les objets subissent une certaine déformation. Lorsque le choc est élastique, les objets retrouvent rapidement leur forme d'origine.

Index des articles

• 1 Conservation de l'énergie cinétique
• 2 amortisseurs élastiques en une dimension
  • 2.1 -Formules pour les collisions élastiques
• 3 Cas particuliers dans les collisions élastiques
  • 3.1 Deux masses identiques
  • 3.2 Deux masses identiques, dont l'une était initialement au repos
  • 3.3 Deux masses différentes, dont l'une initialement au repos
• 4 Coefficient de restitution ou règle de Huygens-Newton
• 5 exercices résolus
  • 5.1 -Exercice résolu 1
  • 5.2 -Exercice résolu 2
  • 5.3 -Exercice résolu 3
  • 5.4 - Exercice résolu 4
• 6 Références

Conservation de l'énergie cinétique

Normalement, lors d'un accident, une partie de l'énergie des objets est dépensée pour la chaleur, la déformation, le son et parfois même la production de lumière. Ainsi, l'énergie cinétique du système après la collision est inférieure à l'énergie cinétique d'origine.

Lorsque l'énergie cinétique K est conservée alors:

K_{ou alors} = K_F

Ce qui signifie que les forces agissant lors de la collision sont conservatrices. Lors de la collision, l'énergie cinétique est brièvement transformée en énergie potentielle, puis de nouveau en énergie cinétique. Les énergies cinétiques respectives varient, mais la somme reste constante.

Les collisions parfaitement élastiques sont rares, bien que les boules de billard soient une assez bonne approximation, tout comme les collisions qui se produisent entre des molécules de gaz parfaits..

Chocs élastiques dans une dimension

Examinons une collision de deux particules de ceci dans une seule dimension; c'est-à-dire que les particules en interaction se déplacent, par exemple, le long de l'axe des x. Supposons qu'ils aient des masses m₁ Oui m_deux. Les vitesses initiales de chacun sont ou alors₁ Oui ou alors_deux respectivement. Les vitesses finales sont v₁ Oui v_deux.

On peut se passer de la notation vectorielle, puisque le mouvement est effectué le long de l'axe x, cependant, les signes (-) et (+) indiquent la direction du mouvement. A gauche est négatif et à droite positif, par convention.

-Formules pour les collisions élastiques

Pour la quantité de mouvement

m₁ou alors₁ + m_deuxou alors_deux = m₁v₁ + m_deuxv_deux

Pour l'énergie cinétique

½ m₁ou alors^deux₁ + ½ m_deuxou alors^deux_deux = ½ m₁v^deux₁ +  ½ m_deuxv^deux_deux

Pourvu que les masses et les vitesses initiales soient connues, les équations peuvent être regroupées pour trouver les vitesses finales.

Le problème est qu'en principe, il faut effectuer une algèbre un peu fastidieuse, car les équations d'énergie cinétique contiennent les carrés des vitesses, ce qui rend le calcul un peu fastidieux. L'idéal serait de trouver des expressions qui n'en contiennent pas.

La première chose est de se passer du facteur ½ et de réorganiser les deux équations de manière à ce qu'un signe négatif apparaisse et que les masses puissent être factorisées:

m₁ou alors₁ - m₁v₁ = M_deuxv_deux - m_deuxou alors_deux

m₁ou alors^deux₁ - m₁v^deux₁  = + M_deuxv^deux_deux - m_deuxou alors^deux_deux

S'exprimant de cette manière:

m₁(ou alors₁ - v₁ ) = m_deux(v_deux - ou alors_deux)

m₁(ou alors^deux₁ - v^deux₁ ) = m_deux (v^deux_deux - ou alors^deux_deux)

Simplification pour éliminer les carrés des vitesses

Il faut maintenant utiliser le produit somme notable par sa différence dans la seconde équation, avec laquelle on obtient une expression qui ne contient pas les carrés, comme on le voulait à l'origine:

m₁(ou alors₁ - v₁ ) = m_deux(v_deux - ou alors_deux)

m₁(ou alors₁ - v₁ ) (ou alors₁ + v₁ ) = m_deux (v_deux - ou alors_deux) (v_deux + ou alors_deux)

L'étape suivante consiste à remplacer la première équation par la seconde:

m_deux(v_deux - ou alors_deux) (ou alors₁ + v₁ ) = m_deux (v_deux - ou alors_deux) (v_deux + ou alors_deux)

Et quand le terme se répète m_deux(v_deux - ou alors_deux) des deux côtés de l'égalité, ledit terme est annulé et ressemble à ceci:

(ou alors₁ + v₁) = (v_deux + ou alors_deux)

Ou encore mieux:

ou alors₁ - ou alors_deux= v_deux -  v₁

Vitesses finales v₁ et V_deux des particules

Vous disposez maintenant de deux équations linéaires avec lesquelles il est plus facile de travailler. Nous les remettrons les uns sous les autres:

m₁ou alors₁ + m_deuxou alors_deux = m₁v₁ + m_deuxv_deux

ou alors₁ - ou alors_deux= v_deux -  v₁

Multiplier la deuxième équation par m₁ et l'ajout d'un terme à un terme est:

m₁ou alors₁ + m_deuxou alors_deux = m₁v₁ + m_deuxv_deux

m₁ou alors₁ - m₁ou alors_deux= m₁v_deux - m₁ v₁

-

2 m₁ou alors₁ + (m_deux - m₁) ou alors_deux = (m_deux + m₁) v_deux

Et il est déjà possible d'effacer v_deux. Par exemple:

Cas particuliers dans les collisions élastiques

Maintenant que les équations sont disponibles pour les vitesses finales des deux particules, il est temps d'analyser certaines situations particulières.

Deux masses identiques

Dans ce cas m₁ = m_deux = m Y:

v₁ = u_deux

v_deux = u₁

Les particules échangent simplement leurs vitesses après la collision.

Deux masses identiques, dont l'une était initialement au repos

De nouveau  m₁ = m_deux = m et en supposant que ou alors₁ = 0:

v₁ = u_deux

v_deux = 0

Après la collision, la particule qui était au repos acquiert la même vitesse que la particule qui se déplaçait, et celle-ci s'arrête à son tour.

Deux masses différentes, dont une initialement au repos

Dans ce cas, supposons que ou alors₁ = 0, mais les masses sont différentes:

Et qu'est-ce qui se passerait si m₁ est bien plus grand que m_deux?

Il arrive que m₁ est toujours au repos et m_deux revient aussi vite qu'il a frappé.

Coefficient de restitution ou règle de Huygens-Newton

Auparavant, la relation suivante entre les vitesses était dérivée pour deux objets en collision élastique: ou alors₁ - ou alors_deux = v_deux -  v₁. Ces différences sont les vitesses relatives avant et après la collision. En général, pour une collision, il est vrai que:

ou alors₁ - ou alors_deux = - (v₁ -  v_deux)

Le concept de vitesse relative est mieux apprécié si le lecteur s'imagine qu'il est sur l'une des particules et à partir de cette position, il observe la vitesse à laquelle l'autre particule se déplace. L'équation ci-dessus est réécrite comme ceci:

Exercices résolus

-Exercice résolu 1

Une boule de billard se déplace vers la gauche à 30 cm / s, entre en collision frontale avec une autre boule identique se déplaçant vers la droite à 20 cm / s. Les deux billes ont la même masse et la collision est parfaitement élastique. Trouver la vitesse de chaque balle après l'impact.

Solution

ou alors₁ = -30 cm / s

ou alors_deux = +20 cm / s

C'est le cas particulier dans lequel deux masses identiques se heurtent élastiquement dans une dimension, donc les vitesses sont échangées.

v₁ = +20 cm / s

v_deux = -30 cm / s

-Exercice résolu 2

Le coefficient de restitution d'une balle qui rebondit sur le sol est égal à 0,82. Si elle tombe du repos, quelle fraction de sa hauteur d'origine la balle atteindra-t-elle après avoir rebondi une fois? Et après 3 rebonds?

Solution

Le sol peut être l'objet 1 dans l'équation du coefficient de restitution. Et il reste toujours au repos, de sorte que:

Avec cette vitesse, il rebondit:

Le signe + indique qu'il s'agit d'une vitesse ascendante. Et selon lui, le ballon atteint une hauteur maximale de:

Maintenant, il revient au sol avec une vitesse de la même magnitude, mais le signe opposé:

Cela permet d'atteindre une hauteur maximale de:

Revenez au sol avec:

Rebonds successifs

Chaque fois que la balle rebondit et monte, multipliez à nouveau la vitesse par 0,82:

À présent h₃ est environ 30% de h_{ou alors}. Quelle serait la hauteur du 6e rebond sans avoir besoin de faire des calculs aussi détaillés que les précédents?

Serieuse h₆ = 0,82¹² h_{ou alors} = 0,092 h_{ou alors} ou seulement 9% de h_{ou alors}.

-Exercice résolu 3

Un bloc de 300 g se déplace vers le nord à 50 cm / s et entre en collision avec un bloc de 200 g se dirigeant vers le sud à 100 cm / s. Supposons que le choc soit parfaitement élastique. Trouvez les vitesses après l'impact.

Données

m₁ = 300 g; ou alors₁ = + 50 cm / s

m_deux = 200 g; ou alors_deux = -100 cm / s

-Exercice résolu 4

Une masse de m est libérée₁ = 4 kg à partir du point indiqué sur la piste sans frottement, jusqu'à ce qu'il entre en collision avec m_deux = 10 kg au repos. À quelle hauteur m monte-t-il?₁ après la collision?

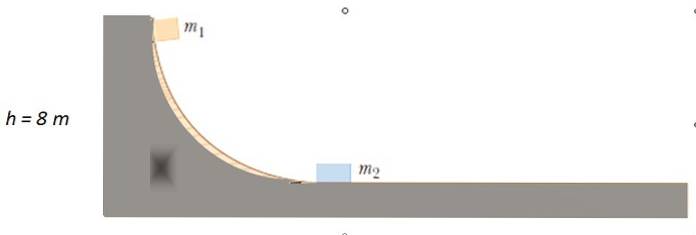
Solution

Puisqu'il n'y a pas de frottement, l'énergie mécanique est conservée pour trouver la vitesse ou alors₁ avec quoi m₁ les impacts  m_deux. Initialement, l'énergie cinétique est égale à 0, car m₁ partie du repos. Lorsqu'il se déplace sur la surface horizontale, il n'a pas de hauteur, donc l'énergie potentielle est de 0.

mgh = ½ mu₁ ^deux

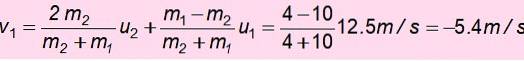
ou alors_deux = 0

Maintenant la vitesse de m₁ après la collision:

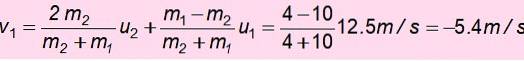
Le signe négatif signifie qu'il a été renvoyé. Avec cette vitesse, il monte et l'énergie mécanique est à nouveau conservée pour trouver h ', la hauteur à laquelle vous pouvez monter après le crash:

½ mv₁^deux = mgh '

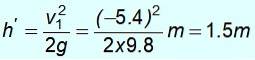
A noter qu'il ne revient pas au point de départ à une altitude de 8 m. Il n'a pas assez d'énergie car la masse a donné une partie de son énergie cinétique m_1.

Les références

1. Giancoli, D. 2006. Physique: principes avec applications. 6^e. Ed Prentice Hall. 175-181
2. Rex, A. 2011. Fondamentaux de la physique. Pearson. 135-155.
3. Serway, R., Vulle, C. 2011. Principes de base de la physique. 9^{n / A} Apprentissage Cengage. 172-182
4. Tipler, P. (2006) Physique pour la science et la technologie. 5e Éd. Volume 1. Éditorial Reverté. 217-238
5. Tippens, P. 2011. Physique: concepts et applications. 7e édition. MacGraw Hill. 185-195