La compressibilité d'une substance ou d'un matériau est le changement de volume qu'il subit lorsqu'il est soumis à un changement de pression. En général, le volume diminue lorsque la pression est appliquée à un système ou à un objet. Cependant, parfois l'inverse se produit: un changement de pression peut produire une explosion dans laquelle le système augmente de volume, ou lorsqu'un changement de phase se produit..
Dans certaines réactions chimiques, cela peut se produire ainsi que dans les gaz, car à mesure que la fréquence des collisions augmente, les forces répulsives se produisent..
Lorsque vous imaginez à quel point il peut être facile ou difficile de comprimer un objet, considérez les trois états dans lesquels la matière se trouve normalement: solide, liquide et gazeux. Dans chacun d'eux, les molécules se tiennent à certaines distances les unes des autres. Plus les liaisons qui joignent les molécules de la substance qui composent l'objet sont fortes et plus elles sont proches, plus il sera difficile de provoquer une déformation.
Un solide a ses molécules très proches les unes des autres, et en essayant de les rapprocher, des forces répulsives apparaissent qui rendent la tâche difficile. On dit donc que les solides ne sont pas très compressibles. Dans les molécules de liquides, il y a plus d'espace, donc leur compressibilité est plus grande, mais même ainsi le changement de volume nécessite généralement de grandes forces.
Les solides et les liquides sont donc difficilement compressibles. Il faudrait une très grande variation de pression pour obtenir un changement de volume appréciable dans des conditions dites normales de pression et de température. D'autre part, les gaz, comme leurs molécules sont largement espacées, sont facilement compressés et décomprimés.
Index des articles
Lorsqu'un objet est immergé dans un fluide par exemple, il exerce une pression sur l'objet dans toutes les directions. De cette façon, nous pouvons penser que le volume de l'objet diminuera, bien que dans la plupart des cas cela ne soit pas appréciable..
La situation peut être vue dans la figure suivante:
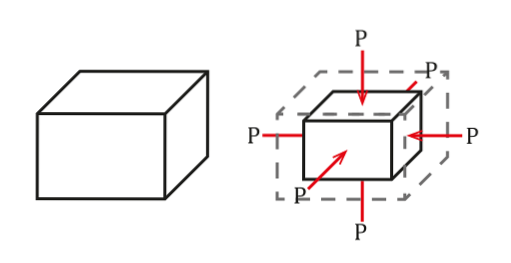
La pression est définie comme une force par unité de surface, qui provoquera un changement de volume ΔV proportionnel au volume initial de l'objet Vou alors. Ce changement de volume dépendra de ses qualités..
La loi de Hooke stipule que la déformation subie par un objet est proportionnelle à la contrainte qui lui est appliquée:
Stress ∝ Strain
La déformation volumétrique subie par un corps est quantifiée par B la constante de proportionnalité requise, appelée la module volumétrique du matériau:
B = -Stress / Strain
B = -ΔP / (ΔV / Vou alors)
Comme ΔV / Vou alors est une grandeur sans dimension, puisque c'est le quotient entre deux volumes, le module volumétrique a les mêmes unités de pression, qui dans le Système International sont les Pascals (Pa).
Le signe négatif indique la réduction de volume attendue, lorsque l'objet est suffisamment comprimé, c'est-à-dire que la pression augmente.
La valeur inverse ou réciproque du module volumétrique est appelée compressibilité et est désigné par la lettre k. Donc:
Ici k est le négatif de la variation fractionnaire de volume par augmentation de pression. Ses unités dans le système international sont les inverses de Pa, c'est-à-dire mdeux / N.
L'équation pour B ou pour k si vous préférez, s'applique à la fois aux solides et aux liquides. Le concept de module volumétrique est rarement appliqué aux gaz. Un modèle simple pour quantifier la diminution de volume qu'un gaz réel peut subir est expliqué ci-dessous..
Une application intéressante est la vitesse du son dans un médium, qui dépend de son module de compressibilité:
Une sphère en laiton massif dont le volume est de 0,8 m3 il est largué dans l'océan à une profondeur où la pression hydrostatique est supérieure de 20 M Pa à celle de la surface. Comment le volume de la sphère changera-t-il? Le module de compressibilité du laiton est connu pour être B = 35 000 MPa,
1 M Pa = 1 mégapascal = 1,10 6 Pennsylvanie
La variation de pression par rapport à la surface est DP = 20 x 10 6 Pa. En appliquant l'équation donnée pour B, on a:
B = -ΔP / (ΔV / Vou alors)
Donc:
ΔV = -5,71,10 -4 x 0,8 m3 = -4,57 x 10-4 m3
La différence de volume peut avoir un signe négatif lorsque le volume final est inférieur au volume initial, donc ce résultat est en accord avec toutes les hypothèses que nous avons faites jusqu'à présent.
Le module de compressibilité très élevé indique qu'un grand changement de pression est nécessaire pour que l'objet subisse une diminution appréciable de volume..
En plaçant votre oreille contre la voie ferrée, vous pouvez savoir quand l'un de ces véhicules s'approche au loin. Combien de temps dure le son lorsque vous voyagez sur un rail en acier si le train est à 1 km?
Densité de l'acier = 7,8 x 10 3 kg / m3
Module de compressibilité de l'acier = 2,0 x 10 Onze Pennsylvanie.
Le module de compressibilité B calculé ci-dessus s'applique également aux liquides, bien qu'un effort important soit généralement requis pour produire une diminution appréciable de volume. Mais les fluides peuvent se dilater ou se contracter lorsqu'ils se réchauffent ou se refroidissent, et également s'ils sont dépressurisés ou sous pression..
Pour l'eau dans des conditions standard de pression et de température (0 ° C et une pression atmosphérique environ ou 100 kPa), le module volumétrique est de 2100 MPa. Autrement dit, environ 21 000 fois la pression atmosphérique.
Pour cette raison, dans la plupart des applications, les liquides sont généralement considérés comme incompressibles. Cela peut être vérifié immédiatement avec une application numérique.
Trouvez la diminution fractionnaire du volume d'eau lorsqu'elle est soumise à une pression de 15 MPa.
Les gaz, comme expliqué ci-dessus, fonctionnent un peu différemment.
Pour savoir de quel volume ils ont n moles d'un gaz donné lorsqu'il est maintenu confiné à une pression P et à une température T, l'équation d'état est utilisée. Dans l'équation d'état pour un gaz parfait, où les forces intermoléculaires ne sont pas prises en compte, le modèle le plus simple indique que:
P.Vidéal = n. R. T
Où R est la constante des gaz parfaits.
Les changements de volume de gaz peuvent être effectués à pression constante ou à température constante. Par exemple, en maintenant la température constante, la compressibilité isotherme ΚT c'est:
Au lieu du symbole «delta» qui était utilisé auparavant lors de la définition du concept de solides, pour un gaz, il est décrit avec une dérivée, dans ce cas une dérivée partielle par rapport à P, en maintenant T constante.
Donc BT le module de compressibilité isotherme est:
Et le module de compressibilité adiabatique B est également important.adiabatique, pour lesquels il n'y a pas de flux de chaleur entrant ou sortant.
Badiabatique = γp
Où γ est le coefficient adiabatique. Avec ce coefficient, la vitesse du son dans l'air peut être calculée:
En appliquant l'équation ci-dessus, trouvez la vitesse du son dans l'air.
Le module de compressibilité adiabatique de l'air est de 1,42 × 105 Pennsylvanie
La densité de l'air est de 1225 kg / m3 (à pression atmosphérique et 15 ºC)
Au lieu de travailler avec le module de compressibilité, en tant que changement d'unité de volume par changement de pression, le facteur de compressibilité d'un gaz réel, un concept différent mais illustratif de la façon dont le gaz réel se compare au gaz parfait:
P. Vréel = Z. R. T
Où Z est le coefficient de compressibilité du gaz, qui dépend des conditions dans lesquelles il se trouve, étant généralement fonction à la fois de la pression P et de la température T, et peut être exprimé par:
Z = f (P, T)
Dans le cas d'un gaz parfait Z = 1. Pour les gaz réels, la valeur Z augmente presque toujours avec la pression et diminue avec la température.
Au fur et à mesure que la pression augmente, les molécules gazeuses entrent en collision plus fréquemment et les forces répulsives entre elles augmentent. Cela peut conduire à une augmentation du volume du gaz réel, où Z> 1.
En revanche, à des pressions plus faibles, les molécules sont libres de se déplacer et les forces d'attraction prédominent. Dans un tel cas, Z < 1.
Pour le cas simple de 1 mole de gaz n = 1, si les mêmes conditions de pression et de température sont maintenues, en divisant les équations précédentes terme par terme, on obtient:
Vréel = Z Vidéal
Il existe un gaz réel à 250 ºK et 15 atm de pression, qui a un volume molaire 12% inférieur à celui calculé par l'équation d'état des gaz parfaits. Si la pression et la température sont maintenues constantes, trouvez:
a) Le facteur de compressibilité.
b) Le volume molaire du gaz réel.
c) Quel type de forces prédomine: attractif ou répulsif?
a) Si le volume réel est inférieur de 12% à l'idéal, cela signifie que:
Vréel = 0,88 Vidéal
Par conséquent, pour 1 mole de gaz, le facteur de compressibilité est:
Z = 0,88
b) Choix de la constante des gaz parfaits avec les unités appropriées pour les données fournies:
R = 0,082 L.atm / mol.K
Le volume molaire est calculé en résolvant et en substituant des valeurs:
c) Les forces d'attraction prédominent, puisque Z est inférieur à 1.
Personne n'a encore commenté ce post.