La conservation de la quantité de mouvement linéaire d'un corps établit que le produit de sa masse et de son vecteur vitesse est une quantité constante, lorsque le corps est libre d'interaction avec d'autres corps et avec la vitesse mesurée par rapport à un référentiel fixe ou non accéléré.
Lorsque vous avez plusieurs corps qui interagissent uniquement entre eux, mais pas avec l'environnement externe, alors le élan linéaire de l'ensemble reste également constant dans le temps.
L'élan linéaire, l'élan ou simplement le élan, est désigné par la lettre p y est une quantité vectorielle:
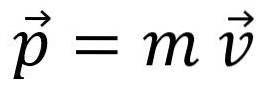
L'élan n'est pas la même chose que la vitesse, bien que la relation soit évidente: par exemple, un camion roulant à 20 km / h a plus d'élan qu'un vélo roulant à la même vitesse.
Pour que la quantité de mouvement linéaire d'un corps change, une force externe nette doit agir sur lui, sinon elle reste constante. Aussi, le moment linéaire P d'un système formé par n-corps est la somme vectorielle des moments individuels:
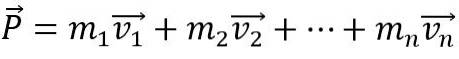
Index des articles
Dans un corps sans force (ou dans lequel toutes les forces sur lui s'annulent), il arrive que le moment linéaire reste constant.
Il en va de même dans un système formé de plusieurs corps qui n'interagissent qu'entre eux, mais pas avec l'environnement extérieur: l'élan linéaire total du système reste fixe au cours de l'évolution du mouvement de l'ensemble..
Ce principe de conservation est énoncé comme suit:
L'élan total d'un ensemble de n-corps qui interagissent uniquement les uns avec les autres, mais pas avec l'environnement extérieur, est une quantité invariable dans le temps.
Et mathématiquement, il s'exprime comme suit:
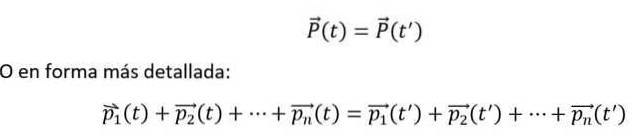
Les égalités ci-dessus sont remplies, si et seulement si le n-les corps interagissent les uns avec les autres, mais pas avec l'environnement extérieur. De plus, les moments individuels doivent toujours être mesurés par rapport à un référentiel inertiel..
Deux astronautes dans l'espace se tiennent la main et sont maintenus dans une position fixe par rapport à l'engin spatial. Mais s'ils se poussent, ils commencent à se séparer dans des directions opposées, vu du navire..
Dans ce cas, comme l'interaction entre les astronautes ne se fait qu'entre eux par la force de contact de leurs mains, l'élan total après poussée est toujours la valeur initiale par rapport à l'engin spatial. Autrement dit, élan total 0.
Cependant, l'élan de chaque astronaute a changé. Au départ, chacun avait 0 moment linéaire par rapport au navire, mais après avoir été poussé, l'un sort dans un sens et l'autre dans le sens opposé, avec des moments linéaires non nuls de même grandeur et de sens opposés..
Ainsi, lorsque les moments individuels sont ajoutés de manière vectorielle, l'impulsion totale initiale est obtenue en conséquence, qui est nulle.
D'autre part, la conservation de la quantité de quantité de mouvement indique que l'astronaute avec la masse la plus faible est celui qui se déplace le plus vite par rapport à l'engin spatial. Mais le résultat de la multiplication de sa masse par sa vitesse est égal au produit obtenu en multipliant la masse de l'autre par la vitesse de l'autre.
Un chiot est sur une plate-forme flottante dans un lac calme et son propriétaire le regarde depuis un quai. Au début, la plate-forme et le chiot sont au repos, mais lorsque le chiot veut se rapprocher du propriétaire, la plate-forme s'éloigne du quai.
L'explication de cette observation est justement dans le principe de conservation de la quantité d'impulsion linéaire. Le système se compose du chiot et de la plate-forme.
Le chiot peut marcher sur la plateforme grâce à la force de frottement entre ses pattes et la surface, dans ce cas la force de frottement est une force interne d'interaction entre lui et la plateforme.
L'ensemble est un système isolé, puisque la plate-forme peut se déplacer horizontalement au-dessus du lac, sans aucune résistance au mouvement. Par contre, dans le sens vertical, toutes les forces sont équilibrées et compensées, et l'ensemble n'a aucun mouvement dans cette direction..
Par conséquent, dans cette situation, toutes les hypothèses sont remplies pour que le principe de conservation de l'impulsion linéaire s'applique.
Un esquimau est piégé au centre d'un lac gelé, la glace est si lisse que peu importe ses efforts, l'esquimau glisse et reste toujours au même endroit.
Le seul moyen possible pour l'Esquimau de sortir du lac est pour lui de lancer dans la direction opposée à laquelle il veut déplacer un objet lourd qu'il porte dans son sac à dos (en supposant qu'il en porte un).
La conservation de l'élan linéaire est appliquée pour propulser une fusée dans l'espace extra-atmosphérique où il n'y a pas de forces externes. Dans ce cas, l'impulsion du navire est obtenue en expulsant des gaz à grande vitesse, de sorte que la fusée peut se déplacer dans la direction opposée à laquelle ils ont été éjectés..
Si à l'origine le navire est au repos, lorsqu'il brûle et expulse du carburant, la force de l'expulsion se produit contre le navire lui-même. C'est une force interne entre les gaz et le navire. Il n'y a pas de forces externes et donc la conservation de l'impulsion linéaire s'applique.
Comme l'impulsion linéaire des gaz est la même et opposée à celle du navire, il parvient à sortir du repos, et en continuant à expulser des gaz, il augmente sa quantité de mouvement et donc sa vitesse.
Un autre cas d'application de la conservation de l'élan linéaire dans la vie quotidienne consiste à enfoncer un clou dans le bois, en tirant parti de la quantité de mouvement ou de l'élan du marteau..
On pourrait faire valoir que dans ce cas, le principe ne s'applique pas, car il y a une force extérieure: la résistance que le bois offre au clou..
Cependant, au moment du contact, la force que le marteau impose sur le clou est une force interne (entre le système qu'est le clou et le marteau) bien supérieure à la résistance à laquelle le bois s'oppose, et donc cette dernière est négligeable.
Tout l'élan du marteau, qui est assez important en raison de sa grande masse et de sa vitesse, est transféré au clou juste après la collision. Notez que tout le moment, mais pas toute l'énergie cinétique du marteau est transférée, car une partie de celle-ci est transformée en énergie thermique dans le clou et dans le marteau, qui élèvent leur température après l'impact..
Les astronautes Andrew et Berenice sont à l'extérieur de la station spatiale se tenant les deux mains et au repos par rapport à la station. Ils sont propulsés en poussant les mains de l'un contre l'autre et ils sont libérés. Si André, 70 kg de masse, se déplace à 1 m / s par rapport à la station, quelle est la vitesse de Bérénice avec 49 kg de masse?
Dans ce cas, les hypothèses de conservation de l'impulsion linéaire s'appliquent clairement, car il n'y a pas de forces externes dans l'espace extra-atmosphérique. La force avec laquelle les deux astronautes poussent leurs mains est une force interne.
Supposons que la masse d'Andrew soit Mà et celle de Bérénice Mb. De même, les vitesses des deux après l'impulsion sont Và pour Andrew et Vb pour Bérénice. Ensuite, la conservation de l'impulsion linéaire s'applique comme ceci:
Mà∙0 + Mb∙0 = Mà∙Và+ Mb∙Vb
En résolvant la vitesse de Bérénice, nous avons:
Vb = - (Mà / Mb) ∙ Và
Placement des valeurs numériques:
Vb = - (70/49) ∙ (1m / s) ou alors = -1,43 m / s ou alors
Autrement dit, Bérénice se déplace à une vitesse de 1,43 m / s dans la direction opposée à celle d'Andrew.
Un chiot de masse 5 kg est au repos sur une plate-forme de 15 kg qui flotte, également au repos, sur un lac immobile. Si le chiot commence à marcher sur la plate-forme à une vitesse de 0,5 m / s par rapport à elle. Quelle sera la vitesse du chiot et de la plate-forme par rapport à un observateur fixé au sol??
Le système de référence inertiel sera considéré comme le quai où se trouve le propriétaire du chiot. Au départ, le chiot et la plate-forme flottante sont au repos par rapport au quai..
Lorsque le chiot décide de marcher rapidement vers le propriétaire v ' par rapport à la plate-forme, la plate-forme s'éloigne de la jetée avec une vitesse +V. La vitesse du chiot par rapport au ressort est obtenue au moyen de la somme vectorielle de sa vitesse par rapport à la plate-forme plus la vitesse de la plate-forme et nous la désignons par:
v = -v' + V
La résistance de l'eau au mouvement de la plate-forme étant pratiquement nulle en raison de sa faible vitesse, on peut affirmer que le système constitué de le chiot + la plateforme est un système isolé et le principe de conservation de l'impulsion linéaire s'applique:
0 = m ∙ v + M ∙ V
En nous rappelant que v = v '+ V nous avons:
0 = -m ∙ v '+ m ∙ v + M ∙ V
Soit: m ∙ v '= (m + M) ∙ V
Donc V = [m / (m + M)] v 'et v = - (M / m) V = - [M / (m + M)] v'
En remplaçant les valeurs numériques que nous avons:
V = [5 / (5 +15)] ∙ 0,5 m / s = 0,125 m / s
Il s'agit de la vitesse à laquelle la plate-forme s'éloigne du quai.
V = - (15/20) ∙ 0,5 m / s = -0,375 m / s
Et c'est la vitesse à laquelle le chiot s'approche du quai.
Personne n'a encore commenté ce post.