le cercle unitaire est un cercle de rayon égal à 1, qui est généralement centré au point (0,0) du système de coordonnées cartésien xy. Utilisé pour définir facilement les rapports trigonométriques des angles à l'aide de triangles rectangles.
L'équation du cercle unité centré à l'origine est:
Xdeux + Ouideux = 1
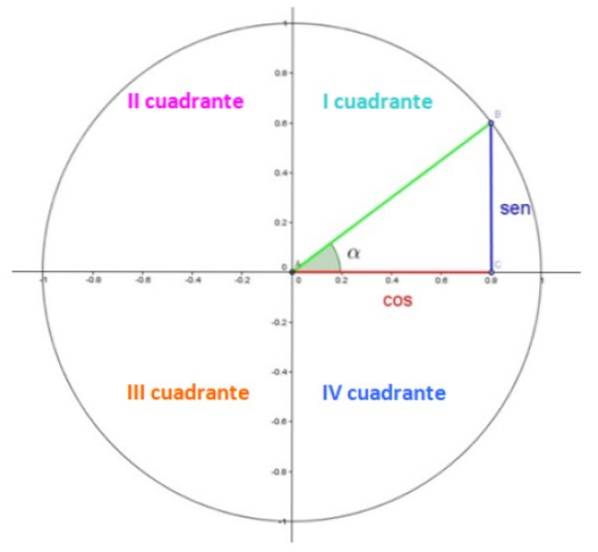
Dans la figure 1, nous avons le cercle unitaire, dans lequel chaque quartier est dans un quadrant. Les quadrants sont numérotés avec des chiffres romains et comptés dans le sens antihoraire.
Dans le premier quadrant, il y a un triangle. Les pattes, en rouge et bleu, mesurent respectivement 0,8 et 0,6, tandis que l'hypoténuse en vert mesure 1, puisqu'il s'agit d'un rayon.
L'angle aigu α est un angle central en position standard, ce qui signifie que son sommet coïncide avec le point (0,0) et son côté initial avec l'axe x positif. L'angle est mesuré dans le sens antihoraire et se voit attribuer un signe positif par convention.
Eh bien, dans le cercle unitaire, les coordonnées cosinus et sinus de α sont respectivement les coordonnées x et y du point B, qui dans l'exemple illustré sont 0,8 et 0,6.
À partir de ces deux, ils sont définis:
Index des articles
Si nous nous limitons aux triangles rectangles, les rapports trigonométriques ne s'appliqueraient qu'aux angles aigus. Cependant, à l'aide du cercle unitaire, le calcul des rapports trigonométriques est étendu à tout angle α.
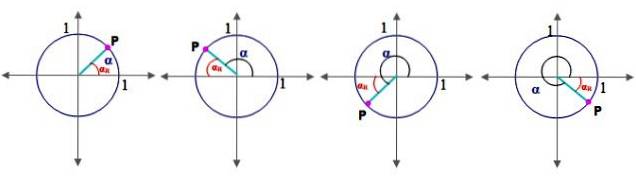
Pour cela, il faut d'abord définir la notion d'angle de référence αR:
Soit α un angle en position standard (celui dont côté de départ coïncide avec l'axe x positif), son angle de référence αR est entre les siens côté terminal et l'axe des abscisses. La figure 2 montre l'angle de référence pour les angles dans les quadrants I, II, III et IV.
Pour chaque quadrant, l'angle de référence est calculé comme ceci:
-Premier quadrant: αR = α
-Deuxième quadrant: αR = 180 ° - α
-Troisième quadrant: αR = α - 180 °
-Quatrième quadrant: αR = 360 ° - α
Notez que le premier quadrant de l'angle α coïncide avec son angle de référence. Eh bien, les rapports trigonométriques de l'angle α sont les mêmes que leur angle de référence, avec les signes correspondant à ceux des quadrants dans lesquels tombe le côté terminal de α..
En d'autres termes, les rapports trigonométriques cosinus et sinus de l'angle α coïncident avec les coordonnées du point P, selon la figure 2.
Dans la figure suivante, nous voyons les rapports trigonométriques de certains angles notables, tels que déduits du cercle unitaire.
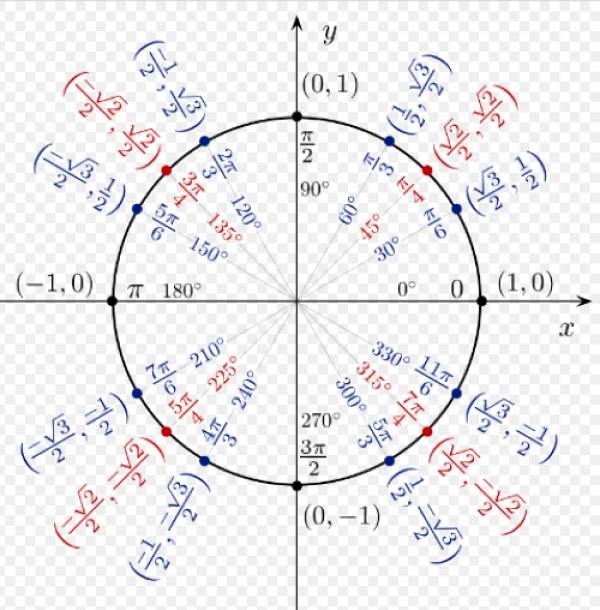
Les rapports cosinus et sinus de tout angle dans le quadrant I sont tous positifs. Pour α = 60º on a les coordonnées (1/2; √3 / 2), qui correspondent respectivement à cos 60º et sin 60º.
Les coordonnées de α = 120º sont (-1/2; √3 / 2), car étant dans le deuxième quadrant, la coordonnée x est négative.
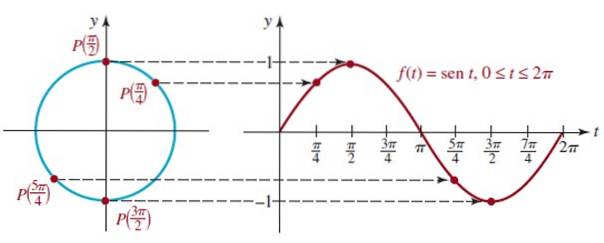
A l'aide du cercle unité et des coordonnées des points P dessus, il est possible de dessiner les graphes des fonctions cos t et sin t, comme nous le verrons ci-dessous.
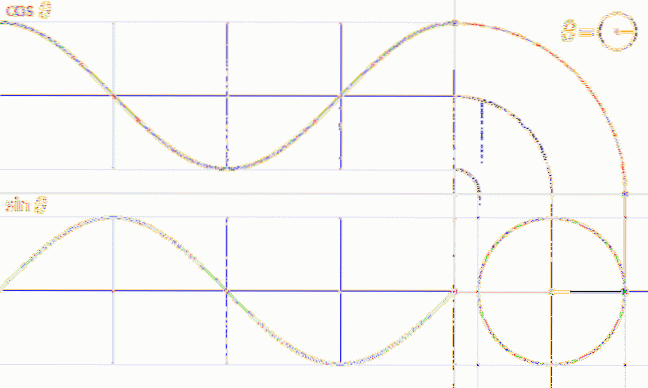
Pour ce faire, différentes positions du point P (t) sont situées sur le cercle unité. Nous allons commencer par le graphe de la fonction f (t) = sin t.
On voit que quand on passe de t = 0 à t = π / 2 (90º) la valeur de sin t augmente jusqu'à atteindre 1, qui est la valeur maximale.
Par contre, de t = π / 2 à t = 3π / 2 la valeur de sin t décroît de 1, passant par 0 à t = π jusqu'à atteindre son minimum de -1 à t = 3π / 2.
La figure montre le graphique du premier cycle de f (t) = sin t qui correspond au premier tour du cercle unité, cette fonction est périodique de période 2π.
Une procédure analogue peut être effectuée pour obtenir le graphe de la fonction f (t) = cos t, comme le montre l'animation suivante:
-Les deux fonctions sont continues dans l'ensemble des nombres réels et également périodiques, de période 2π.
-Le domaine des fonctions f (t) = sin t et f (t) = cos t sont tous des nombres réels: (-∞, ∞).
-Pour la plage ou le chemin du sinus et du cosinus, nous avons l'intervalle [-1,1]. Les crochets indiquent que -1 et 1 sont inclus.
- Les zéros de sin t sont les valeurs qui correspondent à nπ avec n entier, tandis que les zéros de cos t sont [(2n + 1) / 2] avec n également entier.
-La fonction f (t) = sin t est impaire, elle a une symétrie autour de l'origine tandis que la fonction cos t est paire, sa symétrie est autour de l'axe vertical.
Étant donné cos t = - 2/5, qui est la coordonnée horizontale du point P (t) sur le cercle unitaire dans le deuxième quadrant, obtenir la coordonnée verticale correspondante sin t.
Puisque P (t) appartient au cercle unité, dans lequel il est vrai que:
Xdeux + Ouideux = 1
Donc:
y = ± √ 1 - xdeux
Puisque P (t) est dans le deuxième quadrant, la valeur positive sera prise. La coordonnée verticale du point P (t) est y:
y = √ 1 - (-2/5)deux = √0.84
Un modèle mathématique de la température T en degrés Fahrenheit un jour donné, t heures après minuit, il est donné par:
T (t) = 50 + 10 sin [(π / 12) × (t - 8)]
Avec t compris entre 0 et 24 heures. Trouve:
a) La température à 8 heures du matin.
b) Heures pendant lesquelles T (t) = 60 ° F
c) Températures maximales et minimales.
Nous substituons t = 8 dans la fonction donnée:
T (8) = 50 + 10 sin [(π / 12) × (t-8)] = 50 + 10 sin [(π / 12) × (8-8)] =
= 50 + 10 x sin 0 = 50 ºF
50 + 10 sin [(π / 12) × (t-8)] = 60
C'est une équation trigonométrique et nous devons résoudre pour l'inconnu "t":
10 sin [(π / 12) × (t-8)] = 60 - 50 = 10
sin [(π / 12) × (t-8)] = 1
Nous savons que sin π / 2 = 1, donc l'argument sinus doit être 1:
(π / 12) × (t-8) = π / 2
t-8 = 6
t = 14 h
On en conclut qu'à 14 heures après minuit, la température est de 60 °, soit 14 heures. Il n'y a pas d'autre moment de la journée (24 heures) où cela se produit.
La température maximale correspond à la valeur à laquelle sin [(π / 12) × (t-8)] = 1 et est de 60ºF. Par contre, le minimum se produit si sin [(π / 12) × (t-8)] = -1 et est de 40 ° F.
Personne n'a encore commenté ce post.