Quelle est la période de la fonction y = 3sen (4x)?

le période de la fonction y = 3sen (4x) est 2π / 4 = π / 2. Pour bien comprendre la raison de cet énoncé, la définition de la période d'une fonction et la période de la fonction sin (x) doivent être connues; un peu sur la représentation graphique des fonctions sera également utile.

Les fonctions trigonométriques, telles que sinus et cosinus (sin (x) et cos (x)), sont très utiles en mathématiques et en ingénierie.

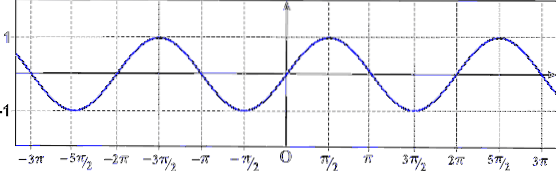
Le mot période fait référence à la répétition d'un événement, donc dire qu'une fonction est périodique équivaut à dire «son graphe est la répétition d'un morceau de courbe». Comme on peut le voir sur l'image précédente, la fonction sin (x) est périodique.

Fonctions périodiques

Une fonction f (x) est dite périodique s'il existe une valeur réelle p ≠ 0 telle que f (x + p) = f (x) pour tout x dans le domaine de la fonction. Dans ce cas, la période de la fonction est p.

La période de la fonction est généralement appelée le plus petit nombre réel positif p qui satisfait la définition.

Comme on peut le voir sur le graphique précédent, la fonction sin (x) est périodique et sa période est de 2π (la fonction cosinus est également périodique, avec une période égale à 2π).

Modifications dans le graphe d'une fonction

Soit f (x) une fonction dont le graphe est connu, et soit c une constante positive. Qu'arrive-t-il au graphique de f (x) si f (x) est multiplié par c? En d'autres termes, quel est le graphique de c * f (x) et f (cx)?

Graphique de c * f (x)

Lors de la multiplication d'une fonction, en externe, par une constante positive, le graphe de f (x) subit une modification des valeurs de sortie; autrement dit, le changement est vertical et il y a deux cas:

- Si c> 1, alors le graphique subit un étirement vertical avec un facteur de c.

- Oui 0

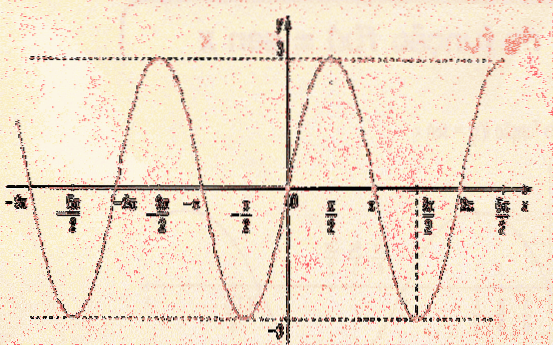
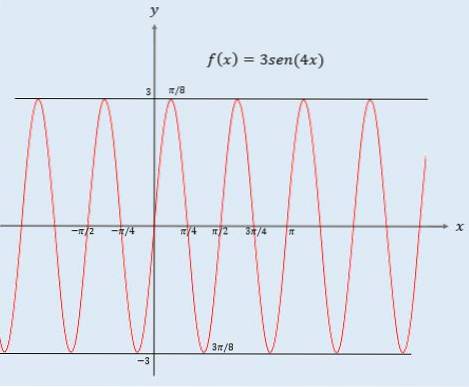
Graphique de f (cx)

Lorsque l'argument d'une fonction est multiplié par une constante, le graphe de f (x) subit une modification des valeurs d'entrée; c'est-à-dire que le changement est horizontal et, comme auparavant, il peut y avoir deux cas:

- Si c> 1, alors le graphe subit une compression horizontale avec un facteur de 1 / c.

- Oui 0

Période de la fonction y = 3sen (4x)

Il est à noter que dans la fonction f (x) = 3sen (4x), il y a deux constantes qui modifient le graphe de la fonction sinus: l'une se multipliant en externe et l'autre en interne..

Le 3 qui est en dehors de la fonction sinus, ce qu'il fait, c'est allonger la fonction verticalement d'un facteur de 3. Cela implique que le graphique de la fonction 3 sin (x) sera entre les valeurs -3 et 3.

Le 4 à l'intérieur de la fonction sinus provoque une compression horizontale du graphique de la fonction d'un facteur 1/4.

En revanche, la période d'une fonction est mesurée horizontalement. Puisque la période de la fonction sin (x) est 2π, en considérant sin (4x) la taille de la période changera.

Pour savoir quelle est la période de y = 3sen (4x), il suffit de multiplier la période de la fonction sin (x) par 1/4 (le facteur de compression).

En d'autres termes, la période de la fonction y = 3sin (4x) est 2π / 4 = π / 2, comme on peut le voir dans le dernier graphique.

Les références

1. Fleming, W., et Varberg, D. E. (1989). Mathématiques du précalcul. Prentice Hall PTR.
2. Fleming, W., et Varberg, D. E. (1989). Mathématiques précalculeuses: une approche de résolution de problèmes (2, éd. Illustré). Michigan: Prentice Hall.
3. Larson, R. (2010). Précalcul (8 éd.). Apprentissage Cengage.
4. Pérez, C. D. (2006). Précalcul. Éducation Pearson.
5. Purcell, E. J., Varberg, D. et Rigdon, S. E. (2007). Calcul (Neuvième éd.). Prentice Hall.
6. Saenz, J. (2005). Calcul différentiel avec fonctions transcendantes précoces pour la science et l'ingénierie (Deuxième édition éd.). Hypoténuse.
7. Sullivan, M. (1997). Précalcul. Éducation Pearson.