Avant de savoir combien de centièmes tiennent dans un dixième les notions de dixième et de centième devraient être clarifiées. Le concept dont découlent ces mots est celui de fraction décimale.
Les utilisations des fractions décimales sont plus courantes que vous ne pouvez l'imaginer. Ils peuvent être appliqués du prix d'un produit dans un magasin, au poids d'un panier de fruits dans le supermarché.
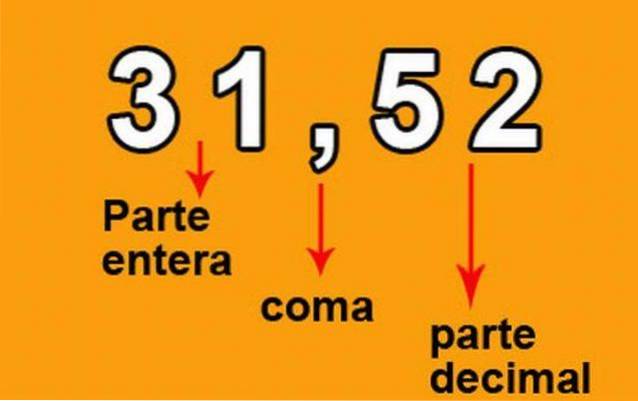
La virgule dans l'image est appelée «point décimal», mais dans la bibliographie anglaise et nord-américaine, un «point» est utilisé à la place de la virgule.
Index des articles
Une fraction décimale est une fraction dont le dénominateur est 10, 100, 1 000, 10 000 ou toute autre puissance de 10, d'où le mot décimal. Par exemple 2/10 000, 53/10, 2781/100, 321/1 000 sont des fractions décimales.
Lorsqu'une fraction décimale est écrite, le dénominateur est omis et un signe (un point décimal) est placé pour indiquer la valeur du nombre.
Dans le nombre du numérateur et à droite de la virgule, il doit y avoir autant de nombres que de zéros dans le dénominateur correspondant.
- 2/10 000 s'écrirait 0,0002.
- 53/10 s'écrirait 5,3.
- 2.781 / 100 s'écrit 27.81.
- 321/1 000 s'écrit 0,321.
En revanche, la fraction qui représente le nombre dans l'image précédente est 3,152 / 100, puisque le nombre a deux chiffres à droite de la virgule décimale.
Le nombre à gauche de la virgule est appelé «partie entière» tandis que le nombre à droite est appelé «partie décimale»..
Tout comme la partie entière d'un nombre est composée d'unités, de dizaines et de centaines nommées de droite à gauche, la partie décimale est également composée de gauche à droite en dixièmes, centièmes et millièmes..
Les dixièmes correspondent au premier chiffre à droite de la virgule décimale et le dénominateur de sa fraction décimale est 10. Par exemple, 3 dixièmes (0,3) équivaut à 3/10.
Par contre, 46/10 équivaut à 46 dixièmes et son écriture décimale est de 4,6, qui peut également être lu comme 4 unités avec 6 dixièmes.
La même chose se produit avec les centièmes (deuxième chiffre à droite de la virgule décimale) et les millièmes (troisième chiffre à droite de la virgule décimale), dont les dénominateurs dans la fraction décimale sont respectivement 100 et 1000..
Avec ce qui est écrit ci-dessus, on sait qu'un dixième équivaut à 1/10 et qu'un centième vaut 1/100. En notation décimale, nous aurons qu'un dixième vaut 0,1 et un centième vaut 0,01.
La clé pour répondre à cette question est de savoir combien de fois ajouter un centième avec lui-même, de sorte que le résultat ne soit qu'un dixième.
Si nous effectuons les calculs, on verra qu'il faut ajouter 1 centième 10 fois à lui-même pour obtenir un dixième.
Par conséquent, 10 centièmes tiennent dans un dixième.
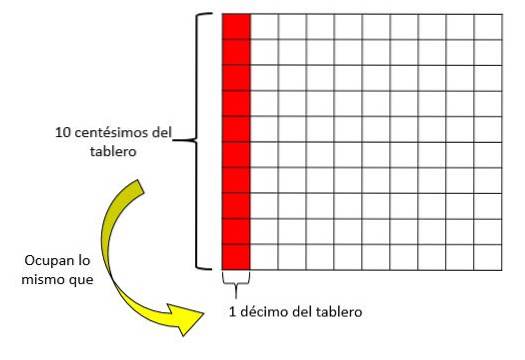
Un autre processus que nous pouvons utiliser pour savoir combien de centièmes tiennent dans un dixième est le suivant: un tableau de 100 carrés est pris, puis 1 carré sur le tableau représente un centième tandis que toute colonne (ou ligne) de 10 carrés représente 1 dixième de la planche.
Donc, pour remplir une ligne (1 dixième), il faut 10 carrés (10 centièmes).
Personne n'a encore commenté ce post.