La densité La masse d'une substance est le quotient entre la masse de l'échantillon et le volume qu'il occupe, son unité de mesure étant le kg / m3 dans le Système international d’unités. La lettre grecque ρ (rho) est souvent utilisée pour le désigner.
La densité de l'eau, qui est le fluide universel, est de 1000 kg / m3 ou 1 g / cm3 à 25 ºC, car la densité subit des changements avec la température et la pression.
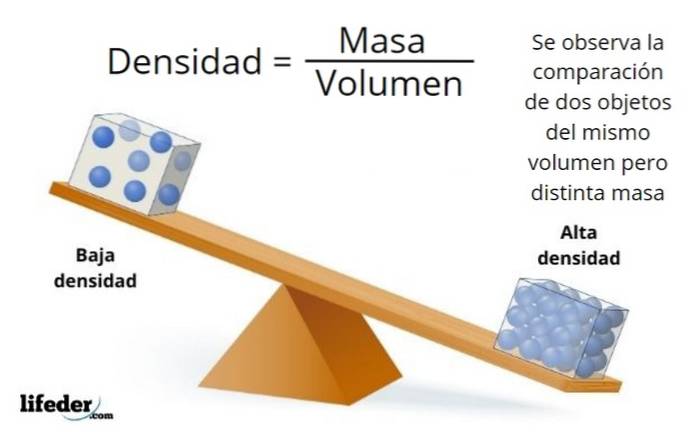
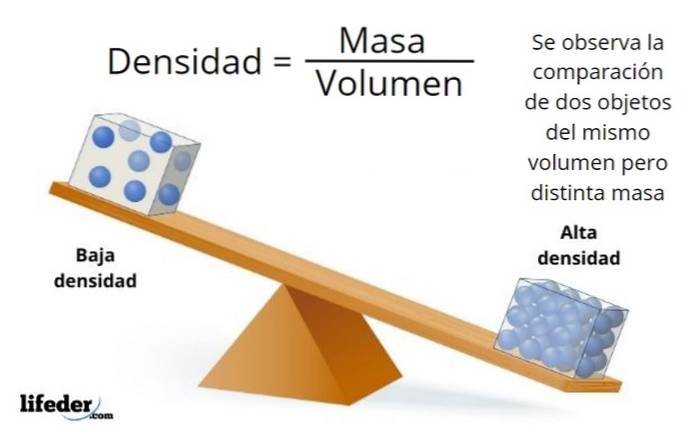
Plusieurs fois, des objets de mêmes dimensions sont trouvés, et pourtant certains sont plus légers et d'autres plus lourds, cela est dû à des différences de densité. L'objet le plus léger a une densité plus faible que le plus lourd.
La densité est une propriété intensive de la matière, qui ne dépend pas de la quantité de masse de l'échantillon examiné, car c'est le rapport masse / volume qui reste constant pour la même substance. Cela permet de différencier une substance d'une autre.
Les matériaux ont une large gamme de densités, les plus faibles sont celles des gaz, donc l'unité kg / m3 il est très grand et on préfère les grammes / litre ou g / l. Les autres unités fréquemment utilisées sont les grammes / millilitre ou les grammes / centimètre cube.
Le concept de densité est particulièrement utile lorsque l'on travaille avec des milieux continus tels que des fluides, qu'il s'agisse de gaz ou de liquides..
Selon la définition donnée, la densité a une formule mathématique donnée par:
Où la densité est ρ, m est la masse et V est le volume.
La densité d'un objet peut être calculée si sa masse et son volume ont été préalablement mesurés. Ce dernier n'est pas toujours facile, car l'échantillon peut être irrégulier, cependant il existe plusieurs méthodes.
Si l'échantillon a une forme géométrique régulière, il existe des formules qui permettent de calculer le volume en fonction de ses dimensions. Quant à la masse, elle peut être obtenue à l'aide d'une balance.
Si l'objet n'est pas régulier, son volume peut être déterminé en mesurant le volume déplacé en le submergeant complètement dans un fluide tel que l'eau..
Pour cela, un récipient gradué est utilisé et il est rempli d'un volume exact d'eau V1, puis l'objet est complètement immergé et le nouveau volume V est mesurédeux. Le volume de l'objet est égal à la différence Vdeux - V1.
Pour utiliser cette méthode, la substance échantillon ne doit pas se dissoudre dans l'eau et un récipient gradué de taille appropriée doit être disponible..
Le principe d'Archimède peut être utilisé pour trouver la densité d'un échantillon solide. Le principe stipule qu'un corps partiellement ou totalement submergé dans un fluide subit une force ascendante appelée poussée, dont la magnitude est égale au poids du fluide déplacé lors de la mise en place du corps..
Pour déterminer la densité d'un objet en utilisant le principe d'Archimède, les étapes suivantes sont suivies:
Déterminer la masse mc de l'objet à l'aide d'une échelle.
Remplissez un récipient avec un fluide dont la densité est connue, qui est généralement de l'eau distillée. Cette valeur s'appelle m1.
Immergez complètement l'objet solide dans le récipient avec de l'eau, en veillant à ce qu'il ne touche pas les parois. On observe que le fluide exerce une poussée ET sur le solide vers le haut, et ceci à son tour, par la troisième loi de Newton, exerce une réaction de même ampleur sur l'eau, mais dans le sens opposé.
En pesant l'ensemble, la valeur obtenue, appelée mdeux, sera celle du récipient rempli d'eau plus cette réaction.
À partir de l'équation de densité, nous pouvons exprimer le volume V du corps, qui est égal au volume de fluide déplacé:
La masse du fluide délogé mF C'est simplement:
mF = mdeux −m1
Donc:
C'est la densité telle que définie ci-dessus: le rapport de la masse au volume de l'échantillon.
Appelez aussi gravité spécifique, C'est la densité d'une substance par rapport à une autre qui est prise comme référence. Pour les solides et les liquides, cette substance de référence est l'eau à 4 ° C et 1 atm de pression et pour les gaz, il s'agit de l'air sec. Il est calculé par:
Densité relative = densité du matériau / densité de l'eau
Tant la masse volumique du matériau que celle de l'eau doivent être mesurées dans les mêmes conditions de pression et de température et exprimées dans les mêmes unités..
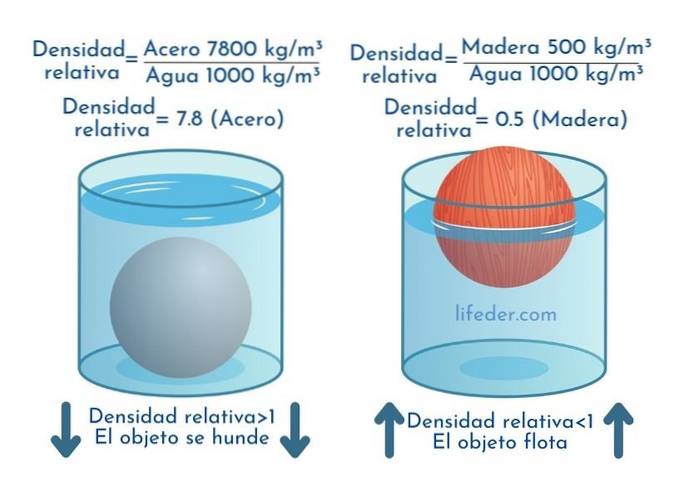
L'image suivante montre les densités relatives de l'acier et du bois.
Puisque la densité de l'acier est de 7800 kg / m3 et celle de l'eau est de 1000 kg / m3, La densité relative de l'acier, notée sg, est:
sg = 7800/1000 = 7,8
Pour sa part, la densité relative du bois est:
sg = 500/1000 = 0,5
Les objets dont la densité relative est inférieure à 1 flottent dans l'eau, tandis que ceux dont la densité relative est supérieure à 1 coulent.
Il est calculé par le quotient entre la masse de l'échantillon et son volume, y compris les pores et les espaces avec de l'air:
Densité apparente = Masse / Volume = (Masse particules + Masse air )/ (Le volume particules+ Le volume air)
Calculer la densité du bouchon, sachant qu'un cube réalisé avec ce matériau, qui mesure 1,5 cm de côté, a une masse de 1 g.
Le volume d'un cube est:
V = ℓ3 = (1,5 cm)3 = 3,375 cm3
L'énoncé indique que la masse m du cube est m = 1 g, par conséquent, en remplaçant les valeurs dans l'équation de densité:
ρ = m / V = 1g / 3,375 cm3 = 0,296 g / cm3
Quelle est la masse d'une sphère en osmium avec un rayon de 15 cm?
À partir de l'équation de densité:
La masse est effacée comme suit:
m = ρ ∙ V
Il est nécessaire de calculer le volume de la sphère, qui est donné par la formule:
Où r est le rayon de la sphère. Puisque la densité de l'osmium est de 22570 kg / m3, Il est pratique d'exprimer les 15 cm en mètres:
r = 15 cm = 15 × 10−2 m
V = (4/3) π × (15 × 10−2 m)3 = 0,01414 m3
Cette valeur est remplacée dans le jeu de la masse:
m = ρ ∙ V = 22570 kg / m3 × 0,01414 m3 = 319,1 kg
Personne n'a encore commenté ce post.