
Caractéristiques de distribution uniforme continue, exemples, applications
Une variable aléatoire a un distribution uniforme continue si la probabilité qu'il prenne une valeur, dans un intervalle fini [a, b], est la même pour tout sous-intervalle de longueur égale.
Cette distribution est analogue à la distribution uniforme discrète, qui attribue la même probabilité à chaque résultat de l'expérience aléatoire, mais dans ce cas la variable à considérer est continue. Par exemple, l'expérience qui consiste à sélectionner un nombre réel au hasard, entre les valeurs a et b, suit la distribution uniforme. Voici son graphique:
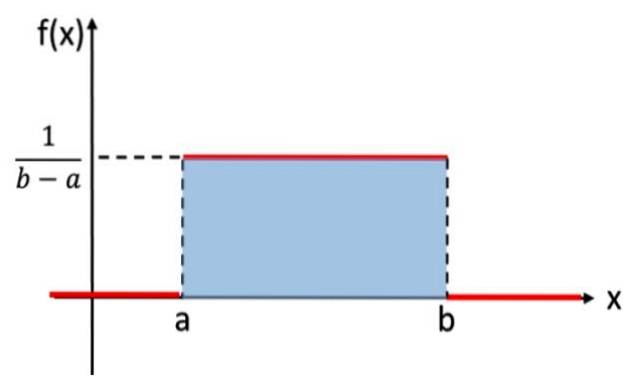
En notation mathématique, la distribution uniforme continue a une fonction de densité définie comme une fonction par morceaux ou par morceaux, qui peut s'écrire:
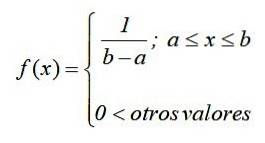
Le graphique de cette fonction, appelé courbe de densité ou fonction, est un rectangle, donc la distribution uniforme continue est également connue sous le nom de disposition rectangulaire y est la plus simple des distributions continues.
La zone sous le graphique d'une distribution de probabilité est égale à 1 et prend toujours des valeurs positives. La distribution uniforme répond à ces critères. Il n'est pas nécessaire d'intégrer directement pour vérifier que l'aire est égale à 1, car l'aire du rectangle ombré de la figure 1 peut être calculée à l'aide de la formule:
Aire = base x hauteur = (b - a) x [1 / (b - a)] = 1
Connaître l'aire sous la courbe de densité est très important, car il existe une relation entre l'aire et la probabilité d'occurrence d'un événement, qui pour cette distribution est déterminée dans la section suivante.
Caractéristiques de la distribution uniforme continue
La distribution uniforme continue se caractérise par:
Fonction de densité
Soit X la variable aléatoire continue, qui appartient à l'intervalle [a, b], alors:

Fonction de distribution
La fonction de distribution calcule la probabilité que la variable aléatoire X prenne une valeur x parmi les valeurs possibles de l'intervalle [a, b]. Pour une distribution continue, il est généralement calculé comme ceci:

Dans le cas de la distribution uniforme continue, ladite probabilité F (x) est égale à l'aire du rectangle dont la base est (x-a) et sa hauteur est (b-a):

Mathématiquement, si F (x) = Pr (X = x) la fonction suivante est établie par parties, selon le résultat précédent:

De cette manière, ce qui a été dit précédemment est vérifié: la probabilité ne dépend que de la valeur de (x-a) et non de sa localisation dans l'intervalle [a, b]. Le graphique de la fonction de distribution est:
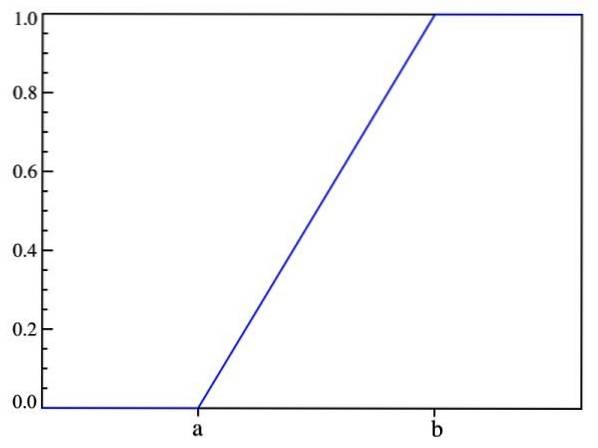
Valeur attendue, variance et écart type
Après avoir fait de nombreuses expériences avec la variable aléatoire continue, sa valeur moyenne est appelée valeur attendue, est noté E (X) et est calculé par l'intégrale suivante:

V (X) = E (Xdeux) - EX)deux
Donc:


D (X) = √ V (X)

Médiane, mode, symétrie et kurtosis
On peut facilement vérifier que la médiane, qui est la valeur centrale de la distribution uniforme, est égale à la moyenne, et puisqu'il n'y a pas de valeur qui se répète plus que d'autres, puisque toutes sont également probables dans l'intervalle [a, b] , la mode n'existe pas.
En ce qui concerne la symétrie, la distribution uniforme est symétrique et le kurtosis, qui est le degré de concentration des valeurs autour du centre, est de -6/5.
Exemples
Diverses situations peuvent être modélisées par distribution continue, et ainsi leur comportement peut être prédit. Voici quelques exemples:
Exemple 1
Une entreprise qui fournit un service électrique fournit des niveaux de tension uniformément répartis, entre 123,0 V et 125,0 V. Cela signifie que dans la prise domestique, il est possible d'obtenir n'importe quelle valeur de tension appartenant à cette plage..
Ainsi, comme vu ci-dessus, le graphique de la fonction de densité est le rectangle en rouge:

Le calcul de la probabilité d'avoir une tension dans l'intervalle donné est très facile, par exemple, quelle est la probabilité que l'entreprise envoie une tension inférieure à 123,5 V?
Cette probabilité est égale à l'aire du rectangle ombrée en bleu:
P (X<123.5) = (123.5 −123.0)x 0.5 = 0.25
Et quelle est la probabilité que la tension délivrée soit supérieure à 124,0 V?
La surface totale étant égale à 1, la probabilité recherchée est:
P (X> 124,0 V) = 1 - (1 × 0,5) = 0,5
Cela a du sens, puisque 124,0 est précisément la valeur au centre de l'intervalle.
Exemple 2
Une certaine variable aléatoire X a une distribution uniforme dans l'intervalle [0,100]. Décider:
a) La probabilité que la valeur de X soit inférieure à 22.
b) La probabilité que X prenne des valeurs entre 20 et 35.
c) La valeur attendue, la variance et l'écart type de cette distribution.
Réponds à
Il est déterminé de la même manière que dans l'exemple précédent, mais il faut d'abord déterminer la hauteur du rectangle, en se rappelant que la surface totale doit être égale à 1:
Aire = 100 × hauteur = 1
Par conséquent, le rectangle a une hauteur égale à 1/100 = 0,01
P (X<22) = 22×0.01 = 0.22
Réponse b
La probabilité demandée est égale à l'aire du rectangle dont la largeur est (35-20) et dont la hauteur est 0,01:
P (22 Si vous préférez accéder directement à la fonction de distribution donnée ci-dessus, il vous suffit de substituer les valeurs dans: P (20≤X≤35) = F (35) -F (20) Avec F (x) donné par: F (x) = (x-a) / (b-a) Les valeurs à saisir sont: a = 0 b = 100 F (35) = (35-0) / (100-0) = 0,35 F (20) = (20-0) / (100-0) = 0,20 P (20≤X≤35) = 0,35-0,20 = 0,15 La valeur attendue est: E (X) = (a + b) / 2 = (100 + 0) / 2 = 50 La variance est: V (X) = (b-a)deux/ 12 = (100-0)deux/ 12 = 833,33 Et l'écart type est: D (X) = √833,33 = 28,87 Cette distribution est utile lors de la réalisation de processus de simulation statistique ou lorsque l'on travaille sur des événements dont la fréquence d'occurrence est régulière.. Certains langages de programmation génèrent des nombres aléatoires entre 0 et 1, et comme le montrent les exemples précédents, la distribution de probabilité suivie est uniforme. Dans ce cas, l'intervalle à considérer est [0,1]. Si vous avez une expérience dans laquelle les événements ont une régularité, comme expliqué précédemment, vous pouvez, en principe, attribuer à chacun la même probabilité d'occurrence. Dans ce cas, le modèle probabiliste de distribution uniforme fournit des informations pour l'analyse.. La distribution uniforme est également utilisée pour arrondir les différences entre les valeurs observées et les valeurs réelles d'une variable, en supposant une distribution uniforme de l'erreur dans un intervalle donné, selon l'arrondissement, généralement de -0,5 à +0,5.Réponse c
Applications
Génération de nombres aléatoires
Échantillonnage de distributions arbitraires
Arrondir les erreurs
Les références



Personne n'a encore commenté ce post.