
Conditions d'équilibre translationnel, exemples, exercices
Un objet est censé être dans équilibre translationnel lorsque la somme des forces agissant sur elle est nulle. Cela ne veut pas dire qu'il y a forcément du repos, mais le mouvement, s'il existe, serait rectiligne uniforme ou exclusivement rotatif, dans le cas d'un gros objet..
Les conditions d'équilibre mécanique sont basées sur les lois de la mécanique de Newton. En effet, la première loi nous dit qu'un objet est au repos ou se déplace avec un mouvement rectiligne uniforme MRU, à condition qu'aucune force nette n'agisse sur lui..

Or, la force nette ou la force résultante est simplement la somme vectorielle de toutes les forces agissant sur l'objet. Selon la deuxième loi de Newton, cette somme doit être égale au produit entre la masse et l'accélération, mais si l'objet n'est pas accéléré, cette somme s'évanouit.
Et en l'absence d'accélération, il y a les deux possibilités précitées: le corps est au repos, c'est-à-dire qu'il ne bouge pas, ou s'il le fait, il doit être avec MRU. Dans le premier cas, on parle d'équilibre transnational statique, et dans le second, de dynamique.
L'équilibre translationnel est un facteur important dans de nombreux aspects de l'ingénierie, par exemple dans la construction. Les éléments qui composent un bâtiment: poutres, câbles, charpentes et plus, doivent être en équilibre pour garantir la stabilité de l'enceinte.
L'équilibre translationnel est également recherché dans les structures mobiles, telles que les escaliers mécaniques, les tapis roulants et dans la pratique de nombreux sports..
Index des articles
- 1 Condition d'équilibre translationnel
- 1.1 Diagrammes du corps libre
- 2 Exemples d'équilibre translationnel
- 2.1 Bâtiments et routes
- 2.2 Livres et objets sur les étagères
- 2.3 Le mobilier
- 2.4 Feux de circulation
- 2.5 Éclairage public
- 3 Exercice résolu
- 3.1 Solution
- 4 Références
Condition d'équilibre translationnel
Supposons que plusieurs forces agissent sur un corps, que nous désignons par F1, Fdeux, F3... . Fn, en utilisant des caractères gras pour mettre en évidence le fait que les forces sont des vecteurs et doivent être ajoutées en tant que telles.
La somme vectorielle de toutes ces forces est appelée force résultante ou alors force nette. Si cette sommation aboutit au vecteur nul, la condition d'équilibre translationnel est remplie:
F1+ Fdeux+ F3... .+ Fn = 0
Cette condition peut être écrite de manière compacte en utilisant la notation de sommation:
∑ Fje = 0
En termes de composantes de la force résultante, l'équation ci-dessus, qui est vectorielle, peut être décomposée en trois équations scalaires, une pour chaque composante de la force résultante:
∑ Fix = 0; ∑ FOui = 0 et ∑ Fz = 0
En pratique, il n'est pas facile d'annuler la somme des forces, car le frottement est une force de contact entre des surfaces qui n'est guère complètement annulée par une autre force..
C'est la raison pour laquelle les objets réels ne sont presque jamais exempts de forces externes, et par conséquent, il est difficile d'obtenir l'équilibre translationnel.
Les ingénieurs utilisent donc des mécanismes pour réduire les frottements, tels que les roulements et l'utilisation d'huiles lubrifiantes..
Diagrammes de corps libre
Le diagramme du corps libre est un diagramme dans lequel les forces agissant sur le corps sont dessinées. Lors de la recherche d'un équilibre translationnel, ces forces doivent être équilibrées. Par exemple, si une force verticale dirigée vers le bas agit, comme un poids, alors il doit y avoir une force verticale ascendante qui a exactement la même magnitude.
Cette force peut être fournie par la main qui supporte l'objet pour qu'il ne tombe pas, une corde ou simplement la surface d'une table.
S'il y a une force tangentielle à la surface, comme un frottement cinétique ou statique, il doit y avoir une autre force opposée pour que l'équilibre existe. Par exemple, regardons le poids suspendu aux chaînes montrées dans la figure suivante.
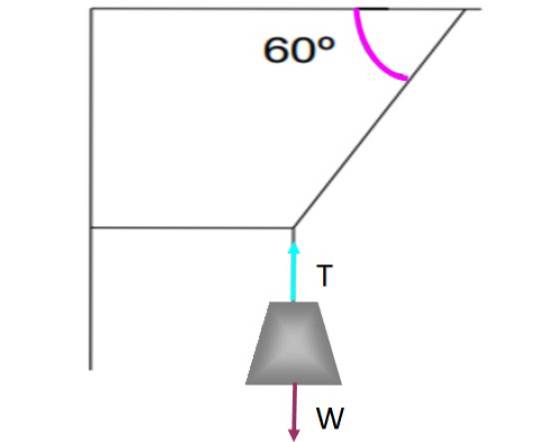
Le poids est maintenu en équilibre de translation et sans bouger, grâce à la corde verticale qui le maintient en exerçant une tension T qui compense le poids W. Chaque force a été représentée sur le poids par une flèche, chacune de taille égale et de même sens, mais de sens opposé..
La force d'équilibrage
Supposons qu'un ensemble de forces agisse sur un objet. C'est ce qu'on appelle un système de force à partir de laquelle la résultante peut être trouvée comme expliqué ci-dessus: en ajoutant de manière vectorielle chacune des forces du système.
Eh bien, la force opposée à cette résultante s'appelle force d'équilibrage. Si la force résultante est FR et la force d'équilibrage est ET, ensuite:
ET + FR = 0
Donc:
ET = - FR
Exemples d'équilibre translationnel
De nombreux objets que l'on trouve au quotidien, à l'intérieur et à l'extérieur de la maison, sont en équilibre translationnel:
Bâtiments et routes
Les bâtiments et les routes sont construits pour rester stables et ne pas basculer ou s'effondrer. Cependant, dans les gratte-ciel et en général dans les bâtiments très hauts, une certaine flexibilité est nécessaire pour résister à l'action du vent..
Livres et objets sur des étagères
Les livres dans une bibliothèque et les produits dans les rayons des magasins sont des objets qui restent en équilibre translationnel et ne bougent pas..
Les meubles
Le mobilier, la télévision à écran plat et les images au mur, ainsi que les lampes suspendues au plafond, pour ne citer que quelques objets, sont en équilibre translationnel..
Feux de circulation
Les feux de signalisation sont fixés par des poteaux et des câbles, de sorte qu'ils ne tombent pas. Pourtant nous savons que le vent les fait balancer.
Éclairage public
Les lampadaires sont également en équilibre translationnel, fixés sur les lampadaires, comme le lampadaire de l'image principale..
Exercice résolu
Quelle doit être la taille de la force Fs de frottement statique de sorte que la boîte de la figure reste au repos au milieu du plan incliné sous un angle α de 37º? La masse de la boîte est m = 8 kg.
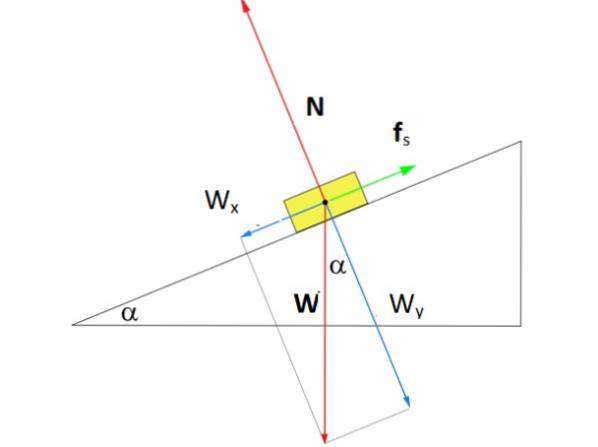
Solution
La figure montre le diagramme du corps libre de la boîte sur le plan. Il y a trois forces qui agissent dessus: le poids W, dirigé verticalement vers le bas, la normale N, qui est la force perpendiculaire exercée par la surface du plan sur la boîte, et enfin la force de frottement statique Fs qui s'oppose au glissement de la boîte en descente.
La condition d'équilibre translationnel stipule que:
W + N + Fs = 0
Mais il faut se rappeler qu'il s'agit d'une somme vectorielle et pour la réaliser il faut décomposer les forces en composantes le long des axes de coordonnées.
Sur la figure, un système de coordonnées a été dessiné dans lequel l'axe des x est parallèle à la surface du plan incliné. Avec ce choix, le frottement statique tombe sur ledit axe, tandis que la normale est sur l'axe y. Le poids est la seule force inclinée et doit être décomposée à l'aide de la trigonométrie:
WX = W. sin α
WOui = W. cos α
La somme des forces le long de chaque axe est:
∑ FOui = N - WOui = 0
∑ FX = fs - WX = 0
De cette dernière équation, il découle que:
Fs = WX
Et comme WX = W. sin α et la grandeur du poids est à son tour W = m.g, où g est la valeur de la gravité, alors la grandeur du frottement statique est simplement:
Fs = m⋅g⋅sen α = 8 kg × 9,8 m / sdeux × sin 37º = 47,2 N.
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 2. Dynamique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. 7ma. Éd. Cengage Learning.
- Tippens, P. 2011. Physique: concepts et applications. 7e édition. Mcgraw Hill.


Personne n'a encore commenté ce post.