
Concept d'expérience aléatoire, espace d'échantillonnage, exemples
On parle de expérience aléatoire lorsque l'issue de chaque essai particulier est imprévisible, même si la probabilité d'occurrence d'un résultat particulier peut être établie.
Cependant, il convient de préciser qu'il n'est pas possible de reproduire le même résultat d'un système aléatoire avec les mêmes paramètres et conditions initiales dans chaque essai de l'expérience..

Un bon exemple d'expérience aléatoire est le lancer d'un dé. Même si l'on prend soin de lancer le dé de la même manière, chaque tentative donnera un résultat imprévisible. En fait, la seule chose que l'on puisse dire est que le résultat peut être l'un des suivants: 1, 2, 3, 4, 5 ou 6.
Le tirage au sort d'une pièce est un autre exemple d'expérience aléatoire avec seulement deux résultats possibles: face ou face. Bien que la pièce soit lancée de la même hauteur et de la même manière, le facteur chance sera toujours présent, ce qui entraînera une incertitude à chaque nouvelle tentative..
Le contraire d'une expérience aléatoire est une expérience déterministe. Par exemple, on sait que chaque fois que de l'eau est bouillie au niveau de la mer, la température d'ébullition est de 100 ºC. Mais il n'arrive jamais que, dans les mêmes conditions, le résultat soit parfois 90 ºC, d'autres 12 0 ° C et parfois 100 ºC..
Index des articles
- 1 espace échantillon
- 1.1 Événement ou événement
- 2 exemples
- 2.1 Exemple 1
- 2.2 Exemple 2
- 3 Références
Espace d'échantillon
L'ensemble de tous les résultats possibles d'une expérience aléatoire est appelé espace d'échantillon. Dans l'expérience aléatoire de lancer un dé, l'espace échantillon est:
D = 1, 2, 3, 4, 5, 6.
D'un autre côté, dans le tirage au sort d'une pièce de monnaie, l'espace échantillon est:
M = têtes, tampon.
Événement ou occurrence
Dans une expérience aléatoire, un un événement c'est l'occurrence ou non d'un certain résultat. Par exemple, dans le cas d'un tirage au sort, un événement ou un événement est qu'il se présente.
Un autre événement dans une expérience aléatoire pourrait être le suivant: qu'un nombre inférieur ou égal à trois est lancé sur le résultat d'un dé.
Au cas où l'événement se produirait, l'ensemble des résultats possibles est l'ensemble:
E = 1, 2, 3
À son tour, il s'agit d'un sous-ensemble de l'espace ou de l'ensemble d'échantillons:
M = 1, 2, 3, 4, 5, 6.
Exemples
Voici quelques exemples qui illustrent ce qui précède:
Exemple 1
Supposons que deux pièces soient lancées l'une après l'autre. On demande:
a) Indiquez s'il s'agit d'une expérience aléatoire ou, au contraire, d'une expérience déterministe.
b) Quel est l'espace échantillon S de cette expérience?
c) Indiquez l'ensemble de l'événement A, correspondant au fait que l'expérience se traduit par des têtes et des queues.
d) Calculez la probabilité que l'événement A se produise.
e) Enfin, trouvez la probabilité que l'événement B se produise: aucune tête n'apparaît dans le résultat.
Solution
a) C'est une expérience aléatoire car il n'y a aucun moyen de prédire quel sera le résultat d'un tirage au sort des deux pièces.
b) L'espace d'échantillonnage est l'ensemble de tous les résultats possibles:
S = (c, c), (c, s), (s, c), (s, s)
c) L'événement A, s'il se produit, peut avoir les résultats suivants:
A = (c, s), (s, c)
d) La probabilité que l'événement A se produise est obtenue en divisant le nombre d'éléments de l'ensemble A par le nombre d'éléments de l'ensemble S correspondant à l'espace d'échantillonnage:
P (A) = 2/4 = ½ = 0,5 = 50%
e) L'ensemble des résultats possibles correspondant à l'événement B (n'apparaissant pas en tête dans le résultat) est:
B = (s, s)
Par conséquent, la probabilité que l'événement B se produise dans un essai est le quotient entre le nombre de résultats possibles de B et le nombre total de cas:
P (B) = ¼ = 0,25 = 25%.
Exemple 2
Un sac contient 10 billes blanches et 10 billes noires. Trois billes consécutivement sont sorties du sac au hasard et sans regarder à l'intérieur.
a) Déterminez l'espace échantillon de cette expérience aléatoire.
b) Déterminer l'ensemble des résultats correspondant à l'événement A, qui consiste à avoir deux billes noires après l'expérience.
c) L'événement B consiste à obtenir au moins deux billes noires, déterminer l'ensemble B de résultats pour cet événement.
d) Quelle est la probabilité que l'événement A se produise?
e) Trouvez la probabilité que l'événement B se produise.
f) Déterminez la probabilité que le résultat de l'expérience aléatoire soit que vous ayez au moins une bille noire. Cet événement s'appellera C.

Solution pour
Pour construire l'espace échantillon, il est utile de créer un diagramme arborescent, comme celui illustré à la figure 3:
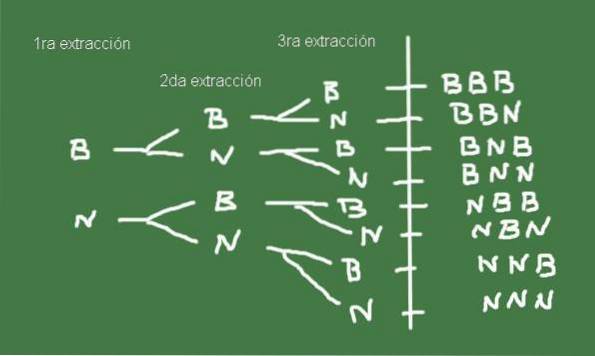
L'ensemble Ω des résultats possibles de l'extraction de trois billes d'un sac avec le même nombre de billes noires et blanches, est précisément l'espace échantillon de cette expérience aléatoire.
Ω = (b, b, b), (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n) , (n, n, b), (n, n, n)
Solution b
L'ensemble des issues possibles correspondant à l'événement A, qui consiste à avoir deux billes noires est:
A = (b, n, n), (n, b, n), (n, n, b)
Solution c
L'événement B est défini comme: «avoir au moins deux billes noires après en avoir tiré au sort trois». L'ensemble des résultats possibles pour l'événement B est:
B = (b, n, n), (n, b, n), (n, n, b), (n, n, n)
Solution d
La probabilité d'avoir l'événement A est le quotient entre le nombre de résultats possibles pour cet événement et le nombre total de résultats possibles, c'est-à-dire le nombre d'éléments dans l'espace d'échantillonnage..
P (A) = n (A) / n (Ω) = 3/8 = 0,375 = 37,5%
Il y a donc 37,5% de chances d'avoir deux billes noires après avoir tiré au hasard trois billes du sac. Mais notez qu'en aucun cas nous ne pouvons prédire le résultat exact de l'expérience.
Solution e
La probabilité que l'événement B se produise, consistant à obtenir au moins une bille noire est:
P (B) = n (B) / n (Ω) = 4/8 = 0,5 = 50%
Cela signifie que la possibilité que l'événement B se produise est égale à la probabilité qu'il ne se produise pas.
Solution f
La probabilité d'obtenir au moins une bille noire, après en avoir extrait trois, est égale à 1 moins la probabilité que le résultat soit "les trois billes blanches".
P (C) = 1 - P (b b b) = 1 - ⅛ = ⅞ = 0,875 = 87,5%
Maintenant, nous pouvons vérifier ce résultat, en notant que le nombre de possibilités que l'événement C se produit est égal au nombre d'éléments des résultats possibles pour l'événement C:
C = (b, b, n), (b, n, b), (b, n, n), (n, b, b), (n, b, n), (n, n, b) , (n, n, n)
n (C) = 7
P (C) = n (C) / n (Ω) = ⅞ = 87,5%
Les références
- CanalPhi. Expérience aléatoire. Récupéré de: youtube.com.
- MateMovil. Expérience aléatoire. Récupéré de: youtube.com
- Pishro Nick H. Introduction à la probabilité. Récupéré de: probabilcourse.com
- Ross. Probabilité et statistiques pour les ingénieurs. Mc-Graw Hill.
- Wikipédia. Expérience (théorie des probabilités). Récupéré de: en.wikipedia.com
- Wikipédia. Événement déterministe. Récupéré de: es. wikipedia.com
- Wikipédia. Expérience aléatoire. Récupéré de: es.wikipedia.com


Personne n'a encore commenté ce post.