
Fractions typiques, exemples, exercices résolus
le fractions ou alors nombres fractionnaires sont les nombres représentés en indiquant le quotient entre deux nombres entiers à Oui b, toujours et quand b est différent de 0. Par exemple, 1/3 est une fraction qui se lit comme suit: «un tiers».
Au numéro à il est connu comme numérateur de la fraction et à b Quoi dénominateur de la même. Le dénominateur nous dit en combien de parties diviser le tout. Pour sa part, le numérateur indique combien de parties de cet ensemble ont été prélevées.

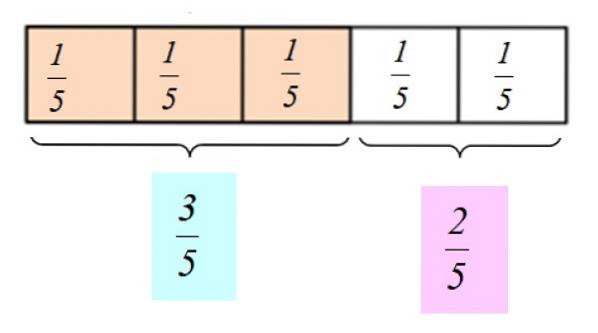
Le tout est tout ce que vous voulez diviser ou diviser, par exemple une pizza ou la barre de chocolat montrée dans la figure 1. La barre est faite de telle manière qu'il est très facile de la diviser en 5 parties égales, où chaque partie est équivalent 1/5 de la barre complète.
Dans la fraction ou le nombre fractionnaire 1/5, le numérateur est 1 et le dénominateur est 5. La fraction se lit "un cinquième".
Supposons que nous mangeons 3 morceaux de chocolat. Nous dirions que nous avons mangé 3/5 parties du bar et qu'il reste 2/5 parties à partager avec un ami. On peut aussi dire que nous avons mangé "les trois cinquièmes du chocolat" et donné "les deux cinquièmes" à notre ami.
La représentation graphique de ces nombres fractionnaires est la suivante:
Index des articles
- 1 Types de fractions
- 1.1 fractions propres
- 1.2 Fractions incorrectes
- 1.3 Fractions apparentes
- 1.4 Fractions équivalentes
- 1.5 Fractions irréductibles
- 1.6 Numéros mixtes
- 2 Exemples de fractions
- 2.1 Achats alimentaires
- 2.2 Recettes de cuisine
- 2.3 Longueurs et diamètres
- 2.4 Intervalles de temps
- 3 Exercices avec des fractions
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 3.3 - Exercice 3
- 3.4 - Exercice 4
- 4 Références
Types de fractions
Fractions appropriées
Une fraction est propre lorsque le numérateur est inférieur au dénominateur et donc sa valeur est inférieure à 1. Les fractions de la section précédente, dans l'exemple du chocolat, sont des fractions propres..
D'autres exemples de fractions propres sont: ½; 8/10; 3/4 et plus.

Fractions incorrectes
Le numérateur des fractions impropres est supérieur au numérateur. Par exemple 4/3, 8/5, 21/10 appartiennent à cette catégorie.
Fractions apparentes
Ces fractions représentent un nombre entier. Parmi eux se trouvent 4/2, 10/5 et 27/3, car si on regarde de près, le résultat de la division du numérateur par le dénominateur de ces fractions donne un nombre entier.
Ainsi: 4/2 = 2, 10/5 = 2 et 27/3 = 9.
Fractions équivalentes
Deux fractions n / m et p / q sont équivalentes lorsque la division du numérateur par le dénominateur donne la même quantité. De cette manière, les fractions équivalentes représentent la même partie du tout..
A titre d'exemple, nous avons les fractions: 15/2 et 30/4. En divisant 15 par 2, vous obtenez 7,5, mais c'est aussi la même chose si vous divisez 30 par 4.
Pour savoir si deux fractions n / m et p / q sont équivalentes, l'égalité suivante est vérifiée:
n * q = m.p
Fractions irréductibles
Lorsque le numérateur et le dénominateur sont tous deux divisés par le même nombre et à condition que le résultat soit un entier, une fraction équivalente à l'original est obtenue, mais avec des nombres plus petits.
Ce processus se poursuit tant que le numérateur et le dénominateur ont exactement le même diviseur. Lorsqu'il n'est pas possible de continuer à diviser, le fraction irréductible de la fraction originale.
L'avantage de travailler avec la fraction irréductible est qu'on obtient une fraction équivalente mais avec des nombres plus petits. C'est pourquoi lorsque vous travaillez avec des fractions, assurez-vous de les réduire autant que possible, pour faciliter les calculs..
Supposons que la fraction 12/20, étant numérateur et dénominateur pair, les deux peuvent être divisés par 2:
12/20 = 6/10
Et encore une fois:
6/10 = 3/5
La fraction 3/5 équivaut à 12/20, mais plus simple.
Numéros mixtes
Une fraction impropre admet également une représentation sous forme de nombre mixte, ainsi appelée parce qu'elle a une partie entière et une autre partie fractionnaire, la partie fractionnaire étant une fraction propre..
Regardons un exemple rapide avec la fraction 15/2 que nous savons égale à 7,5.
Nous pouvons exprimer 15/2 comme un nombre mixte comme ceci:
15/2 = 7 + 0,5
Mais 0,5 = ½. Donc 15/2 = 7 ½ qui se lit "sept et demi".
Exemples de fractions
Les nombres fractionnaires sont nécessaires car les nombres naturels et les entiers sont insuffisants lorsque nous voulons diviser des choses comme la barre chocolatée.
Et c'est pourquoi il existe une variété infinie de modèles de mesure et d'objets dont les spécifications incluent des nombres fractionnaires, sans parler du nombre de situations quotidiennes dans lesquelles ceux-ci sont nécessaires..
Courses alimentaires
Dans les pays où le système métrique est utilisé, il est courant d'utiliser le kilo pour désigner le poids de nombreux aliments. Nous ne voulons pas toujours acheter des quantités entières, mais un peu plus ou un peu moins.
C'est pourquoi nous demandons:
- ½ kg de poisson
- ¾ kg de tomates
- ¼ kilo d'oignon
- 1 ½ kg de pêches (1 kilo et demi).
Et lors de l'utilisation des étalons de mesure anglo-saxons, la même chose se produit: nous avons besoin de 2 livres et demi ou 1/4 de livre de quelque chose.
Tous ces nombres sont fractionnaires et, comme nous l'avons vu, correspondent à deux types différents de fractions: propre et impropre..
Recettes de cuisine
Les recettes de cuisine utilisent souvent des nombres fractionnaires pour indiquer la quantité de certains ingrédients. Par exemple:
- ½ tasse de farine
- ¾ kg de sucre pour préparer un gâteau.
Longueurs et diamètres
Les dimensions des meubles, des pièces textiles et de toutes sortes d'ustensiles ménagers sont mesurées en fractions de mètre ou de pouce, que ce soit en utilisant le système décimal métrique ou anglo-saxon..
Même dans les pays où le système métrique prévaut, les tuyaux commerciaux en cuivre, en acier et autres tuyaux de plomberie ont souvent des diamètres spécifiés en pouces. Également d'autres matériels tels que des vis et des écrous.
Puisqu'un pouce équivaut à 2,54 cm, ces pièces, qui ont des diamètres plus petits, sont généralement exprimées en fractions de pouce..
Les mesures très courantes pour les tuyaux domestiques sont:
- ½ pouce
- ¼ pouce
- 3/8 et 5/8 pouces.
Tranches de temps
Les nombres fractionnaires sont utilisés quotidiennement pour exprimer des intervalles de temps tels que ¼, ½ et ¾ d'heure, voire un peu plus: 1 heure et ¼ et ainsi de suite.

Exercices avec des fractions
- Exercice 1
Aujourd'hui, Juanito a apporté à l'école un gâteau pour son anniversaire et il veut le distribuer à tous ses amis, mais il veut donner au professeur un morceau trois fois plus gros que celui des enfants..
En tenant compte du fait qu'il y a 24 enfants + l'enseignant, à qui vous voulez donner l'équivalent de trois morceaux, en combien de morceaux devez-vous couper le gâteau??
Solution
Si Juanito voulait seulement distribuer le gâteau à ses amis, ils auraient chacun 1/24.
Mais, comme il veut donner une partie à l'enseignant et que la pièce est trois fois plus grande, il devrait distribuer le gâteau entre 24 élèves + 3 pièces pour l'enseignant. En d'autres termes, chaque enfant correspond à 1/27 pièces et le professeur 3/27 pièces.
De plus, si on réduit la fraction 3/27 on obtient que l'enseignant prendra 1/9 du gâteau.
- Exercice 2
Une entreprise avec un patron et trois salariés réalise un chiffre d'affaires de 6 000 € par mois. Combien d'argent chaque personne a-t-elle si le patron veut garder la moitié de ce qu'il a gagné?
Solution
Si le boss veut gagner la moitié, il devra garder 6000/2, ce qui fait 3000 €. Sur les 3 000 € restants, c'est ce que les trois employés devront distribuer. Ainsi, chaque salarié gagnera 3000/3, soit 1000 €.
- Exercice 3
Trouvez la fraction irréductible de:
a) 18/12 et b) 4/11
Solution pour
Dans le premier cas, nous notons que tant le numérateur que le dénominateur sont pairs et divisibles par 2. Ils sont également divisibles par 3, puisque 12 et 18 sont des multiples de ce chiffre..
On peut donc simplifier la fraction en divisant à la fois le numérateur et le dénominateur par 2 ou par 3, l'ordre est indifférent.
En commençant par diviser par 2:
12/18 = 6/9
Maintenant, nous notons que le numérateur et le dénominateur de cette fraction équivalente sont des multiples de 3, donc en divisant les deux par ce chiffre:
6/9 = 2/3
Et comme 2 et 3 sont des nombres premiers, ils n'ont plus d'autre diviseur commun que 1. Nous avons atteint la fraction irréductible.
Le plus grand diviseur commun GCF du numérateur et du dénominateur aurait également pu être calculé. Pour 12 et 18 ans:
GCF (12,18) = 6.
Et puis le numérateur et le dénominateur sont divisés par ce nombre, ce qui équivaut à le faire par étapes.
Solution b
On observe ici que 11 est un nombre premier et que ses diviseurs sont 1 et 11. Pour sa part, 4 admet 4, 2 et 1. À l'exception de 1, ces nombres n'ont pas de diviseur commun et donc la fraction 4/11 est irréductible.
- Exercice 4
Indiquez quelle est la plus grande fraction de chaque paire:
a) ¾ et 5/4
b) 3/7 et 4/9
Solution pour
Lorsque deux fractions positives ont le même dénominateur, la plus grande est celle qui a le plus grand numérateur. Donc 5/4 est plus grand, puisque 5> 3.
Solution b
Si les fractions n / m et p / q ont des dénominateurs différents et sont toutes deux positives, le critère de comparaison est le suivant:
Si n.q> m. p, puis n / m> p / q
Une autre option consiste à trouver l'expression décimale de chaque fraction et à comparer.
Selon le premier critère: n = 3, m = 7, p = 4, q = 9. Donc: n.q = 3 * 4 = 12 et m.p = 7 * 4 = 28.
J'aime 12< 28, ocurre que 3/7 < 4/9.
Ou nous exprimons chaque fraction sous forme décimale, obtenant ceci:
3/7 = 0,428571428… .
4/9 = 0,444444444 ... .
Les points de suspension indiquent que le nombre de décimales est infini. Mais cela suffit pour vérifier qu'en effet, 4/9> 3/7.
Les références
- Baldor, A. 1986. Arithmétique. Éditions et distributions du Codex.
- Carena, M. 2019. Manuel de mathématiques. Université nationale du littoral.
- Figuera, J. 2000. Mathématiques 8. Ediciones Co-Bo.
- Jiménez, R. 2008. Algèbre. Prentice Hall.
- La page Math. Qu'est-ce qu'une fraction? Récupéré de: themathpage.com.

Personne n'a encore commenté ce post.