
Force résultante comment elle est calculée et les exercices sont résolus
La Obliger résultant c'est la somme de toutes les forces qui agissent sur un même corps. Lorsqu'un corps ou un objet est soumis à l'action de plusieurs forces simultanément, un effet se produit. Les forces d'actionnement peuvent être remplacées par une seule force qui produit le même effet. Cette force unique est la force résultante également connue sous le nom de force nette et est représentée par le symbole FR .
L'effet qu'il produit FR cela dépendra de sa taille, de sa direction et de son sens. Les grandeurs physiques qui ont une direction et un sens sont des quantités vectorielles.
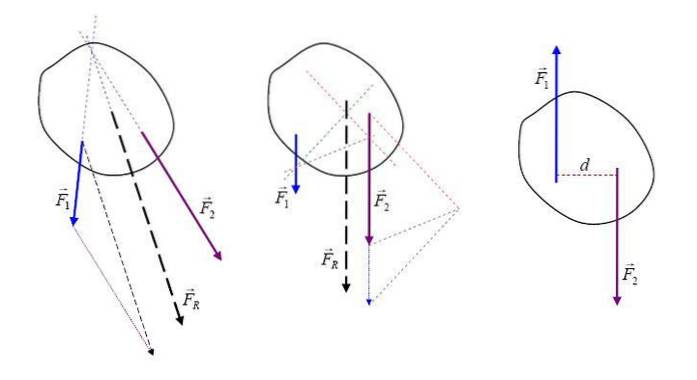
Étant les forces agissant sur les grandeurs d'un vecteur corporel, la force résultante FR est une somme vectorielle de toutes les forces et peut être représentée graphiquement avec une flèche qui indique sa direction et sa direction.
Avec la force résultante, le problème d'un corps affecté par plusieurs forces est simplifié en le réduisant à une seule force agissant.
Index des articles
- 1 formule
- 2 Comment calculez-vous la force résultante?
- 2.1 résultante de forces parallèles
- 2.2 Forces non parallèles
- 3 exercices résolus
- 4 Références
Formule
La représentation mathématique de la force résultante est une sommation vectorielle des forces.
FR= ∑F (1)
∑F = F1+ Fdeux+ F3+... FN (deux)
FR= Force résultante
∑F = Somme des forces
N= Nombre de forces
La force résultante peut également être représentée par la deuxième équation de la loi de Newton.
FR= m.à (3)
m= masse corporelle
a = accélération corporelle
Si l'équation (1) est remplacée dans l'équation (3), les équations suivantes sont obtenues:
∑F = m.à (4)
F1+ Fdeux+ F3+... FN = m.à (5)
Les expressions mathématiques (4) et (5) fournissent des informations sur l'état du corps en obtenant le vecteur d'accélération à.
Comment calculez-vous la force résultante?
La force résultante est obtenue en appliquant la deuxième loi de Newton qui stipule ce qui suit:
La force nette agissant sur un corps est égale au produit de sa masse et de l'accélération qu'il acquiert. (Équation (3))
L'accélération du corps aura la direction de la force nette appliquée. Si toutes les forces agissant sur le corps sont connues, il suffirait de l'ajouter de manière vectorielle pour obtenir la force résultante. De même, si la force résultante est connue alors il suffirait de la diviser par la masse du corps pour obtenir son accélération.
Si la force résultante est nulle, le corps est au repos ou à vitesse constante. Si une seule force agit sur le corps, la force résultante est égale à cette force FR=F.
Lorsque plusieurs forces agissent sur le même corps, les composantes vectorielles de la force doivent être prises en compte, et si ces forces sont parallèles ou non.
Par exemple, si nous faisons glisser horizontalement un livre placé sur une table, les forces dans la direction horizontale sont les seules qui fournissent une accélération au corps. La force verticale nette sur le livre est nulle.
Si la force appliquée au livre a une inclinaison par rapport au plan horizontal de la table, la force est écrite en fonction des composantes verticale et horizontale.
Résultant forces parallèles
Les forces parallèles qui agissent sur un corps sont ces forces qui agissent dans la même direction. Ils peuvent être de deux types de sens égal ou opposé.
Lorsque les forces agissant sur un corps ont la même direction et la même direction ou sont dans la direction opposée, la force résultante est obtenue en effectuant la somme algébrique des valeurs numériques des forces.
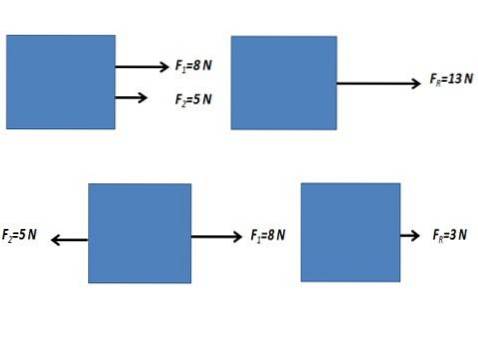
Forces non parallèles
Lorsque des forces non parallèles sont appliquées à un corps, la résultante des forces aura des composantes rectangulaires et verticales. L'expression mathématique pour calculer la force nette est:
FRdeux= (∑ FX)deux+(∑ FOui)deux (6)
donc θX= ∑ FOui / ∑ FX (7)
∑ FX et ∑ FX= Somme algébrique des composants X et Oui des forces appliquées
θX= angle formé par la force résultante FR avec arbre X
Notez que la force résultante de l'expression (6) n'est pas mise en évidence en gras et c'est parce qu'elle n'exprime que la valeur numérique. La direction est déterminée par l'angle θX.
L'expression (6) est valable pour les forces agissant dans le même plan. Lorsque les forces agissent dans l'espace, le composant est pris en compte z de force lors du travail avec des composants rectangulaires.
Exercices résolus
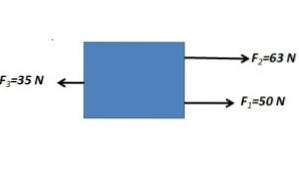
Les forces parallèles dans la même direction sont additionnées et soustraites avec la force parallèle dans la direction opposée
FR= 63 N + 50 N - 35 N = 78N
La force résultante a une magnitude de 78N avec une direction horizontale.
2. Calculez la force résultante d'un corps sous l'influence de deux forces F1 Oui Fdeux. La force F1 il a une magnitude de 70N et est appliqué horizontalement. La force Fdeux a une magnitude de 40 N et est appliqué à un angle de 30 ° par rapport au plan horizontal.
Pour résoudre cet exercice, un diagramme du corps libre est dessiné avec les axes de coordonnées X et Oui
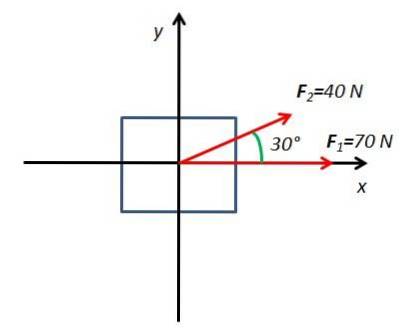
Tous les composants sont déterminés X et Oui des forces agissant sur le corps. La force F1 n'a qu'une seule composante horizontale sur l'axe X. La force Fdeux il a deux composants F2x et F2 et qui sont obtenues à partir des fonctions sinus et cosinus de l'angle 30 °.
F1 fois = F1=70N
F2x = Fdeux cos 30 ° = 40 N.cos 30 ° = 34,64 N
F1 an = 0
F2 et= Fdeux sans 30 ° = 40 sans 30 ° = 20N
∑ FX =70N + 34,64N = 104,64N
∑ FOui=20N + 0 = 20N
Une fois que les forces résultantes dans l'arbre ont été déterminées X et Oui on procède à l'obtention de la valeur numérique de la force résultante.
FRdeux= (∑ FX)deux+(∑ FOui)deux
La force résultante est la racine carrée de la somme des composantes au carré des forces
FR= √ (104,64 N)deux+(20N)deux
FR= 106,53 N
L'angle formé par la force résultante FR est obtenu à partir de l'expression suivante:
θX= donc-1(∑ FOui / ∑ FX)
θX= donc-1(20N / 104,64 N) = 10,82 °
La force résultante FR a une magnitude de 106,53N et a une direction déterminée par l'angle de 10,82 ° qu'il forme avec l'horizontale.
Les références
- Dola, G, Duffy, M et Percival, A. La physique. Espagne: Heinemann, 2003.
- Avison, J H. Le monde de la physique. Inde: Thomas Nelson and Sons, 1989.
- Pinsent, M. Processus physiques. Royaume-Uni: Nelson Thomas, 2002.
- Yadav, S K. Ingénierie Mécanique. Delhi: Maison d'édition Discovery, 2006.
- Serway, R A et Jewett, J W. Physique pour les scientifiques et les ingénieurs. Californie, États-Unis: Brooks / Cole, 2010.



Personne n'a encore commenté ce post.