
Fonction injective ce que c'est, à quoi ça sert et exemples

Ongle fonction injective est toute relation d'éléments du domaine avec un seul élément du codomaine. Aussi connu sous le nom de fonction un à un ( Onze ), font partie de la classification des fonctions en ce qui concerne la manière dont leurs éléments sont liés.
Un élément du codomaine ne peut être que l'image d'un seul élément du domaine, de cette manière les valeurs de la variable dépendante ne peuvent pas être répétées.
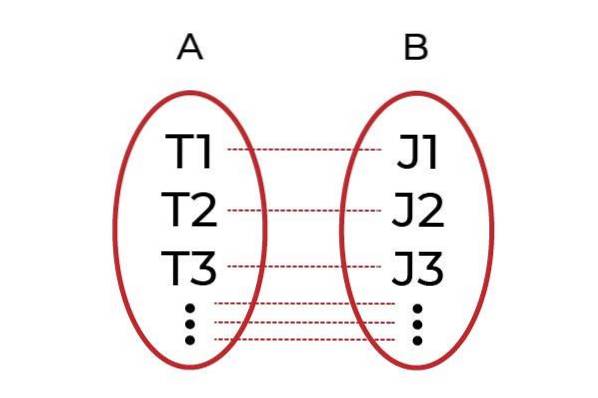
Un exemple clair serait de regrouper les hommes ayant des emplois dans le groupe A et dans le groupe B tous les patrons. La fonction F Ce sera celui qui associera chaque ouvrier à son patron. Si chaque travailleur est associé à un patron différent via F, ensuite F va etre un fonction injective.
À envisager injectif à une fonction, les conditions suivantes doivent être remplies:
∀ x1 ≠ xdeux ⇒ F (x1 ) ≠ F (xdeux )
C'est la manière algébrique de dire Pour tous x1 différent de xdeux vous avez un F (x1 ) différent de F (xdeux ).
Index des articles
- 1 A quoi servent les fonctions d'injection?
- 1.1 Conditionnement fonctionnel
- 2 Exemples de fonctions d'injection avec des exercices résolus
- 2.1 Exemple 1
- 2.2 Exemple 2
- 2.3 Exemple 3
- 2.4 Exemple 4
- 2.5 Exemple 5
- 2.6 Exemple 6
- 2.7 Exemple 7
- 3 exercices proposés en classe / à domicile
- 4 Références
À quoi servent les fonctions injectives?
L'injectivité est une propriété des fonctions continues, puisqu'elles assurent l'affectation d'images pour chaque élément du domaine, aspect essentiel dans la continuité d'une fonction..
Lors du dessin d'une ligne parallèle à l'axe X sur le graphique d'une fonction injective, vous ne devez toucher le graphique qu'en un seul point, quelle que soit la hauteur ou l'amplitude de Oui la ligne est tracée. C'est la manière graphique de tester l'injectivité d'une fonction.
Une autre façon de tester si une fonction est injectif, résout la variable indépendante X en termes de variable dépendante Oui. Ensuite, il faut vérifier si le domaine de cette nouvelle expression contient les nombres réels, en même temps que pour chaque valeur de Oui il y a une valeur unique de X.
Les fonctions ou relations d'ordre obéissent, entre autres, à la notation F: DF→CF
Qu'est-ce qui est lu F à partir de DF jusqu'à CF
Où la fonction F raconter les ensembles Domaine Oui Codomaine. Aussi connu sous le nom de jeu de départ et de jeu d'arrivée.
Le nom de domaine réF contient les valeurs autorisées pour la variable indépendante. Le codomain CF Il est composé de toutes les valeurs disponibles pour la variable dépendante. Les éléments de CF relative à réF sont connus comme Plage de fonctions (RF ).
Conditionnement fonctionnel
Parfois, une fonction non injective peut être soumise à certaines conditions. Ces nouvelles conditions peuvent en faire un fonction injective. Toutes sortes de modifications du domaine et du codomaine de la fonction sont valides, l'objectif étant de remplir les propriétés d'injectivité dans la relation correspondante.
Exemples de fonctions d'injection avec des exercices résolus
Exemple 1
Laissez la fonction F: R → R défini par la ligne F (x) = 2x - 3
R: [Tous les nombres réels]
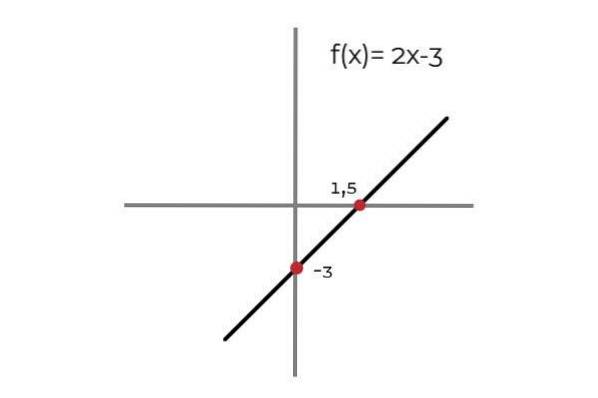
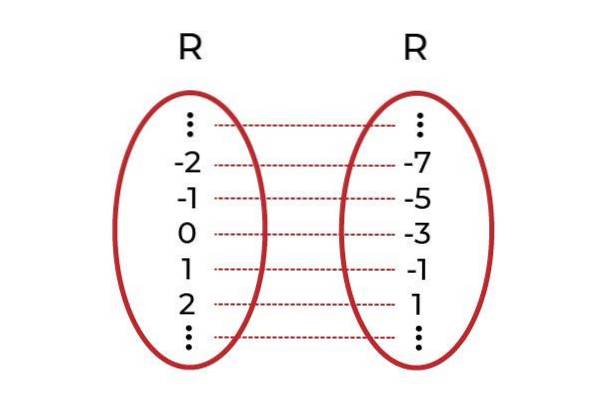
On observe que pour chaque valeur du domaine il y a une image dans le codomaine. Cette image est unique ce qui fait de F une fonction injective. Ceci s'applique à toutes les fonctions linéaires (Fonctions dont le plus grand degré de la variable est un).
Exemple 2
Laissez la fonction F: R → R Défini par F (x) = xdeux +1
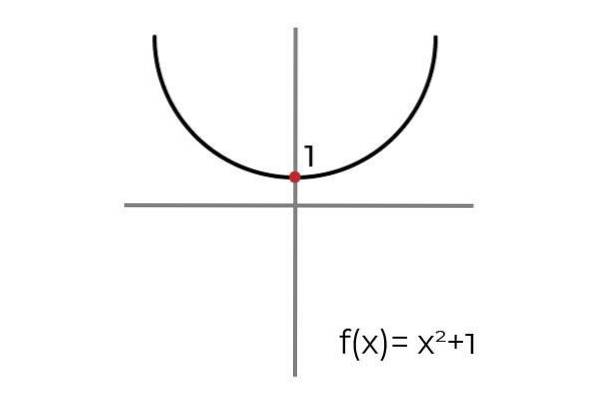
Lors du tracé d'une ligne horizontale, on observe que le graphique se trouve à plusieurs reprises. Pour cette raison, la fonction F il n'est pas injectif tant qu'il est défini R → R
Nous procédons à conditionner le domaine de la fonction:
F: R+ OU ALORS 0 → R
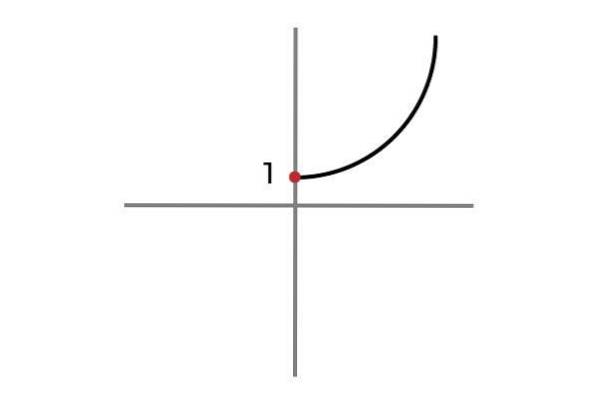
Maintenant, la variable indépendante ne prend pas de valeurs négatives, de cette manière la répétition des résultats est évitée et la fonction F: R+ OU ALORS 0 → R Défini par F (x) = xdeux + 1 est injectif.
Une autre solution homologue serait de limiter le domaine à gauche, c'est-à-dire de restreindre la fonction à ne prendre que des valeurs négatives et nulles.
Nous procédons à conditionner le domaine de la fonction
F: R- OU ALORS 0 → R
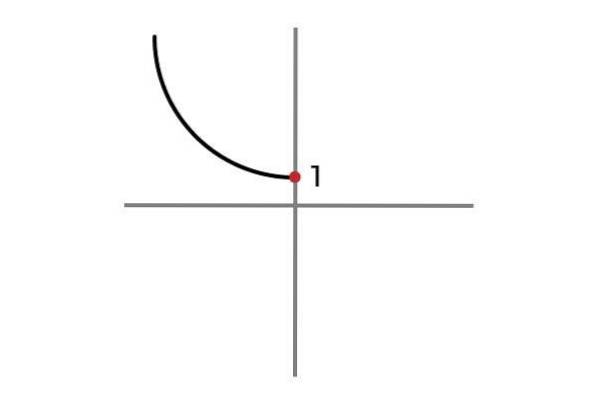
Maintenant, la variable indépendante ne prend pas de valeurs négatives, de cette manière la répétition des résultats est évitée et la fonction F: R- OU ALORS 0 → R Défini par F (x) = xdeux + 1 est injectif.
Les fonctions trigonométriques ont des comportements similaires aux ondes, où il est très courant de trouver des répétitions de valeurs dans la variable dépendante. Grâce à un conditionnement spécifique, basé sur la connaissance préalable de ces fonctions, nous pouvons restreindre le domaine pour répondre aux conditions d'injectivité.
Exemple 3
Laissez la fonction F: [ -π / 2, π / 2 ] → R Défini par F (x) = Cos (x)
Dans l'intervalle [ -π / 2 → π / 2 ] la fonction cosinus varie ses résultats entre zéro et un.
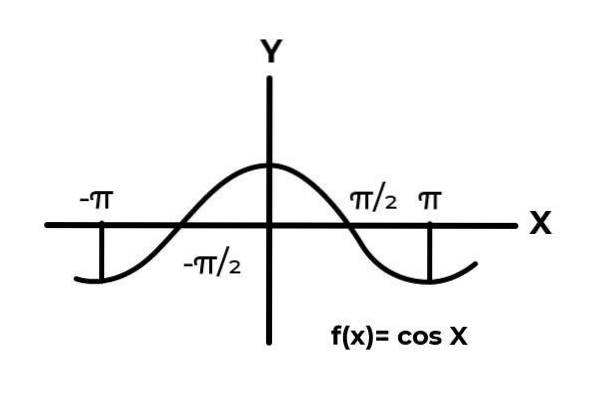
Comme on peut le voir sur le graphique. Partir de zéro dans x = -π / 2 atteignant alors un maximum à zéro. C'est après x = 0 que les valeurs commencent à se répéter, jusqu'à ce qu'elles reviennent à zéro dans x = π / 2. De cette façon, on sait que F (x) = Cos (x) n'est pas injectif pour l'intervalle [ -π / 2, π / 2 ] .
Lors de l'étude du graphique de la fonction F (x) = Cos (x) des intervalles sont observés là où le comportement de la courbe s'adapte aux critères d'injectivité. Comme par exemple l'intervalle
[0 , π ]
Où la fonction varie résulte de 1 à -1, sans répéter aucune valeur dans la variable dépendante.
De cette façon, la fonction fonction F: [0 , π ] → R Défini par F (x) = Cos (x). C'est injectif
Il existe des fonctions non linéaires où des cas similaires se produisent. Pour les expressions de type rationnel, où le dénominateur contient au moins une variable, il existe des restrictions qui empêchent l'injectivité de la relation.
Exemple 4
Laissez la fonction F: R → R Défini par F (x) = 10 / x
La fonction est définie pour tous les nombres réels sauf 0 qui a une indétermination (ne peut être divisé par zéro).
Lorsqu'elle s'approche de zéro à partir de la gauche, la variable dépendante prend de très grandes valeurs négatives, et immédiatement après zéro, les valeurs de la variable dépendante prennent de grandes valeurs positives.
Cette perturbation provoque l'expression F: R → R Défini par F (x) = 10 / x
Ne soyez pas injectif.
Comme on le voit dans les exemples précédents, l'exclusion des valeurs dans le domaine sert à "réparer" ces indéterminations. Nous procédons à exclure zéro du domaine, laissant les ensembles de départ et d'arrivée définis comme suit:
R - 0 → R
Où R - 0 symbolise les réels sauf pour un ensemble dont le seul élément est zéro.
De cette façon, l'expression F: R - 0 → R Défini par F (x) = 10 / x est injectif.
Exemple 5
Laissez la fonction F: [0 , π ] → R Défini par F (x) = Sen (x)
Dans l'intervalle [0 , π ] la fonction sinus varie ses résultats entre zéro et un.
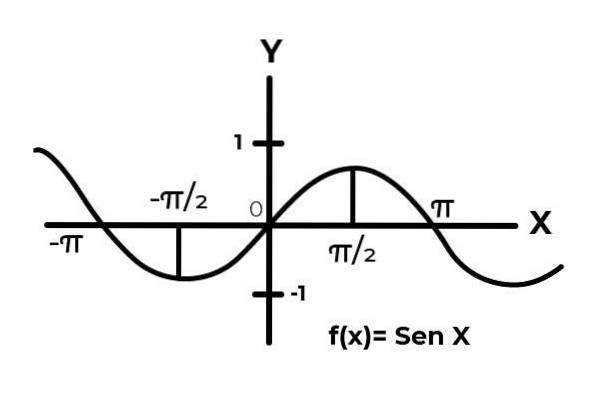
Comme on peut le voir sur le graphique. Partir de zéro dans x = 0 puis atteindre un maximum en x = π / 2. C'est après x = π / 2 que les valeurs commencent à se répéter, jusqu'à revenir à zéro x = π. De cette façon, on sait que F (x) = Sen (x) n'est pas injectif pour l'intervalle [0 , π ] .
Lors de l'étude du graphique de la fonction F (x) = Sen (x) des intervalles sont observés là où le comportement de la courbe s'adapte aux critères d'injectivité. Comme par exemple l'intervalle [ π / 2,3π / 2 ]
Où la fonction varie résulte de 1 à -1, sans répéter aucune valeur dans la variable dépendante.
De cette façon, la fonction F: [ π / 2,3π / 2 ] → R Défini par F (x) = Sen (x). C'est injectif
Exemple 6
Vérifiez si la fonction F: [0, ∞) → R Défini par F (x) = 3xdeux c'est injectif.
Cette fois, le domaine de l'expression est déjà limité. On observe également que les valeurs de la variable dépendante ne se répètent pas dans cet intervalle.
Par conséquent, on peut conclure que F: [0, ∞) → R Défini par F (x) = 3xdeux c'est injectif
Exemple 7
Identifiez laquelle des fonctions suivantes est
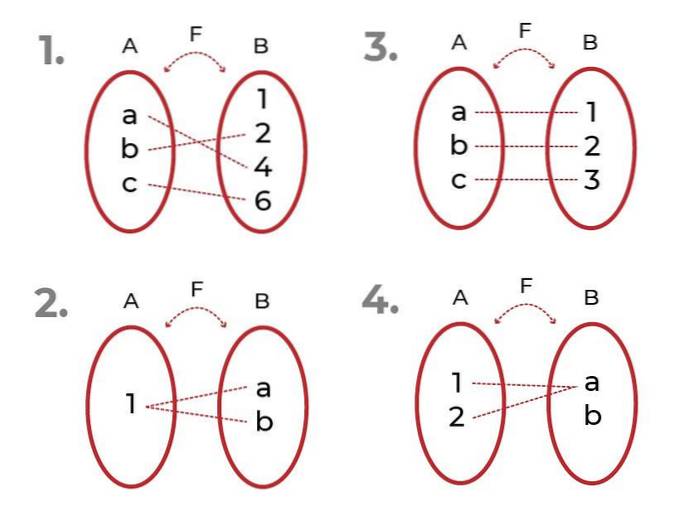
- C'est injectif. Les éléments associés du codomaine sont uniques pour chaque valeur de la variable indépendante.
- Ce n'est pas injectif. Il y a des éléments du codomaine associés à plus d'un élément de l'ensemble de départ.
- C'est injectif
- Ce n'est pas injectif
Exercices proposés pour la classe / à la maison
Vérifiez si les fonctions suivantes sont injectives:
F: [0, ∞) → R Défini par F (x) = (x + 3)deux
F: [ π / 2,3π / 2 ] → R Défini par F (x) = Tan (x)
F: [ -π,π ] → R Défini par F (x) = Cos (x + 1)
F: R → R défini par la ligne F (x) = 7x + 2
Les références
- Introduction à la logique et à la pensée critique. Merrilee H. Salmon. Université de Pittsburgh
- Problèmes en analyse mathématique. Piotr Biler, Alfred Witkowski. Université de Wroclaw. Pologne.
- Éléments d'analyse abstraite. Mícheál O'Searcoid PhD. Département de mathématiques. Collège universitaire de Dublin, Beldfield, Dublind 4.
- Introduction à la logique et à la méthodologie des sciences déductives. Alfred Tarski, New York Oxford. Presse de l'Université d'Oxford.
- Principes de l'analyse mathématique. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelone Espagne.


Personne n'a encore commenté ce post.