La géométrie euclidienne correspond à l'étude des propriétés des espaces géométriques où les axiomes d'Euclide sont satisfaits. Bien que ce terme soit parfois utilisé pour couvrir des géométries qui ont des dimensions plus élevées avec des propriétés similaires, il est généralement synonyme de géométrie classique ou de géométrie plane..
Au IIIe siècle a. C. Euclide et ses disciples ont écrit le Éléments, un travail qui englobe les connaissances mathématiques de l'époque dotées d'une structure logique-déductive. Depuis lors, la géométrie est devenue une science, initialement pour résoudre des problèmes classiques et a évolué pour devenir une science formatrice qui aide à raisonner..
Index des articles
Pour parler de l'histoire de la géométrie euclidienne, il est essentiel de commencer par Euclide d'Alexandrie et la Éléments.
Lorsque l'Égypte a été laissée aux mains de Ptolémée Ier, après la mort d'Alexandre le Grand, il a commencé son projet dans une école d'Alexandrie.
Parmi les sages qui enseignaient à l'école, il y avait Euclide. On suppose que sa naissance date d'environ 325 av. C. et sa mort de 265 à. C. Nous pouvons savoir avec certitude qu'il est allé à l'école de Platon.
Pendant plus de trente ans, Euclide a enseigné à Alexandrie, en construisant ses éléments célèbres: il a commencé à écrire une description exhaustive des mathématiques de son temps. Les enseignements d'Euclide ont produit d'excellents disciples, tels qu'Archimède et Apollonius de Perga.
Euclide était chargé de structurer les découvertes disparates des Grecs de l'Antiquité Éléments, mais contrairement à ses prédécesseurs, il ne se limite pas à affirmer qu'un théorème est vrai; Euclid propose une démonstration.
Les Éléments ils sont un recueil de treize livres. Après la Bible, c'est le livre le plus publié, avec plus d'un millier d'éditions.
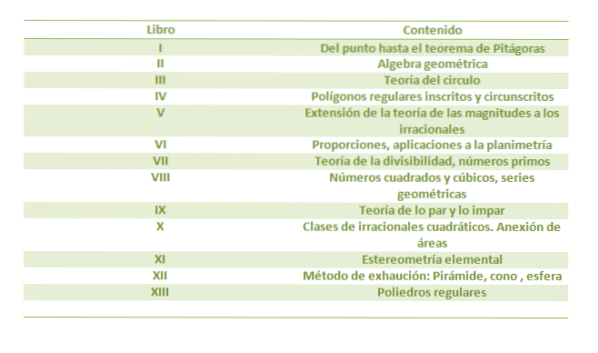
Les Éléments est le chef-d'œuvre d'Euclide dans le domaine de la géométrie, et offre un traitement définitif de la géométrie à deux dimensions (le plan) et à trois dimensions (l'espace), ce qui est à l'origine de ce que nous appelons maintenant la géométrie euclidienne.
Les éléments sont constitués de définitions, de notions communes et de postulats (ou axiomes) suivis de théorèmes, de constructions et de preuves..
- Un point est ce qui n'a pas de parties.
- Une ligne est une longueur sans largeur.
- Une ligne droite est une ligne qui se trouve également par rapport aux points qui se trouvent dans cette.
- Si deux lignes sont coupées de manière à ce que les angles adjacents soient égaux, les angles sont appelés angles droits et les lignes sont appelées perpendiculaires.
- Les lignes parallèles sont celles qui, étant dans le même plan, ne se croisent jamais.
Après ces définitions et d'autres, Euclide nous présente une liste de cinq postulats et de cinq notions..
- Deux choses égales à un tiers sont égales l'une à l'autre.
- Si les mêmes choses sont ajoutées aux mêmes choses, les résultats sont les mêmes.
- Si des choses égales sont soustraites de choses égales, les résultats sont égaux.
- Les choses qui correspondent sont égales les unes aux autres.
- Le total est supérieur à une partie.
- Une et une seule ligne passe par deux points différents.
- Les lignes droites peuvent être prolongées indéfiniment.
- Un cercle peut être dessiné avec n'importe quel centre et n'importe quel rayon.
- Tous les angles droits sont égaux.
- Si une ligne droite croise deux lignes droites de sorte que les angles intérieurs du même côté s'additionnent à moins de deux angles droits, les deux lignes se croisent de ce côté..
Ce dernier postulat est connu sous le nom de postulat parallèle et il a été reformulé comme suit: "Pour un point en dehors d'une ligne, une seule parallèle à la ligne donnée peut être tracée".
Voici quelques théorèmes du Éléments ils serviront à montrer les propriétés des espaces géométriques où les cinq postulats d'Euclide sont remplis; De plus, ils illustreront le raisonnement logique-déductif que ce mathématicien a utilisé.
Si deux triangles ont deux côtés et que l'angle entre eux est égal, alors les autres côtés et les autres angles sont égaux..
Soit ABC et A'B'C 'deux triangles avec AB = A'B', AC = A'C 'et les angles BAC et B'A'C' égaux. Déplaçons le triangle A'B'C 'de sorte que A'B' coïncide avec AB et que l'angle B'A'C 'coïncide avec l'angle BAC.
Ainsi, la ligne A'C 'coïncide avec la ligne AC, de sorte que C' coïncide avec C. Ensuite, d'après le postulat 1, la ligne BC doit coïncider avec la ligne B'C '. Par conséquent, les deux triangles coïncident et, par conséquent, leurs angles et leurs côtés sont égaux.
Si un triangle a deux côtés égaux, alors les angles opposés à ces côtés sont égaux..
Supposons que le triangle ABC a des côtés égaux AB et AC.
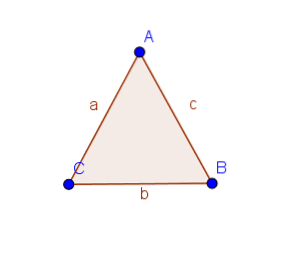
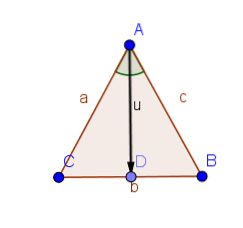
Ainsi, les triangles ABD et ACD ont deux côtés égaux et les angles entre eux sont égaux. Ainsi, d'après la proposition 1.4, les angles ABD et ACD sont égaux.
Vous pouvez construire une ligne parallèle à une ligne donnée par un point donné.
Étant donné une ligne L et un point P, une ligne M est tracée par P et coupe L. Puis une ligne N est tracée par P qui coupe L. Maintenant, une ligne N est tracée par P qui coupe M, formant un angle égal à celui que L forme avec M.
N est parallèle à L.
Supposons que L et N ne soient pas parallèles et se coupent en un point A. Soit B un point de L au-delà de A. Considérons la droite O qui passe par B et P. Ensuite, O coupe M à des angles qui s'additionnent à moins de deux droit.
Alors par 1,5 la ligne O doit couper la ligne L de l'autre côté de M, donc L et O se coupent en deux points, ce qui contredit le postulat 1. Par conséquent, L et N doivent être parallèles.
Personne n'a encore commenté ce post.