
Formule et équations de la loi d'Ampère, preuve, exercices
La Loi d'Ampère déclare que la circulation du vecteur d'induction magnétique B est proportionnelle à l'intensité I du courant qui la traverse.
À son tour, la circulation de B est la somme de tous les produits entre la composante tangentielle B║ et la longueur d'un petit segment Δℓ d'une courbe fermée C, autour d'un circuit. En termes mathématiques, il est écrit comme ceci:
∑ B║ .Δℓ ∝ je
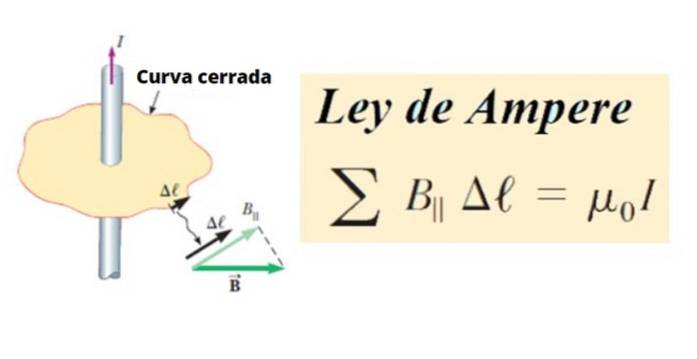
Comme une ligne ou une courbe C arbitraire, elle peut être divisée en petits segments Δℓ, et ceux-ci à leur tour peuvent être infinitésimaux, alors ils sont appelés dℓ.
Dans ce cas, la sommation devient une intégrale linéaire du produit scalaire entre les vecteurs B et ds. Ledit produit contient la composante tangentielle de B, qui est B cosθ, où θ est l'angle entre les vecteurs:
Le petit cercle traversant l'intégrale signifie que l'intégration a lieu sur un chemin fermé C, ce qui dans ce cas implique le courant circulant à travers la section transversale du conducteur.
La constante de proportionnalité nécessaire pour établir l'égalité est μou alors, la perméabilité du vide. De cette manière, la loi d'Ampère est:

La loi d'Ampère nous dit que l'intégrale de ligne ∫C B ∙ ds est exactement μou alorsI, mais cela ne nous donne pas les détails sur l'orientation du champ magnétique B par rapport à la courbe C en chaque point, ni sur la façon de calculer l'intégrale. Il nous dit seulement que le résultat en est toujours μou alorsje.
Index des articles
- 1 Preuve de la loi d'Ampère
- 1.1 Champ magnétique du fil rectiligne et infini
- 2 exercices résolus
- 2.1 - Exercice 1
- 2.2 - Exercice 2
- 3 Références
Démonstration de la loi d'Ampère
La loi d'Ampère est vérifiée expérimentalement en vérifiant le champ magnétique produit par un très long conducteur rectiligne. Avant d'aborder le problème, nous devons mettre en évidence deux cas d'intérêt particulier dans l'équation précédente:
-Le premier est quand B et ds sont parallèles, ce qui signifie que B est tangent à C. Alors l'angle entre les deux vecteurs est de 0 ° et le produit scalaire est simplement le produit des grandeurs B.ds.
-La seconde se produit si B et ds sont perpendiculaires, auquel cas le produit scalaire est égal à 0, puisque l'angle entre les vecteurs est de 90 °, dont le cosinus est 0.
Un autre détail important est le choix de la courbe C sur laquelle la circulation du champ est évaluée. La loi d'Ampère ne précise pas ce qu'elle peut être, mais elle doit impliquer la distribution du courant. Il ne dit pas non plus dans quelle direction parcourir la courbe et il y a deux possibilités pour cela.
La solution est d'attribuer des signes selon la règle du pouce droit. Les quatre doigts sont incurvés dans la direction dans laquelle vous souhaitez intégrer, généralement ce sera le même que le champ B circuler. Si le courant pointe dans la direction du pouce droit, on lui attribue un signe + et sinon, un signe -.
Ceci s'applique lorsqu'il y a une distribution avec plusieurs courants, certains peuvent être positifs et d'autres négatifs. La somme algébrique d'entre eux est celle que nous allons placer dans la loi d'Ampère, qui est généralement nommée courant verrouillé (par courbe C).
Champ magnétique à fil rectiligne infini
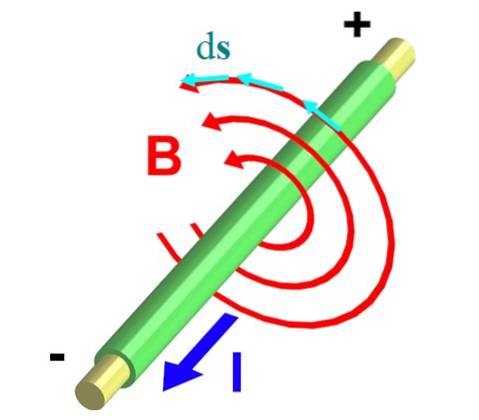
La figure 2 montre un fil transportant un courant I hors du plan. La règle du pouce droit garantit que B circule dans le sens antihoraire, décrivant les circonférences comme indiqué par les flèches rouges.

Prenons l'un d'eux, dont le rayon est r. Nous le divisons en petits segments différentiels ds, représenté par les vecteurs en bleu. Les deux vecteurs, B et ds, sont parallèles en tout point de la circonférence, et donc l'intégrale ∫C B ∙ ds Il se transforme en:
∫C Bds
En effet, comme nous l'avons déjà dit, le produit scalaire B ∙ ds est le produit des grandeurs des vecteurs par le cosinus de 0º. On connaît le résultat de l'intégrale grâce à la loi d'Ampère, on écrit donc:
∫C Bds = μou alorsje
La magnitude du champ étant constante sur toute la trajectoire, il laisse l'intégrale:
B ∫C ds = μou alorsje
L'intégrale ∫C ds représente la somme de tous les segments infinitésimaux qui composent la circonférence du rayon r, équivalent à sa longueur, le produit de son rayon par 2π:
B.2πr = μou alorsje
Et à partir de là, nous constatons que la magnitude de B est:
B = μou alorsI / 2πr
Il convient de souligner que même si le chemin sélectionné (ou circuit ampèreien) n'était pas circulaire, le résultat de l'intégrale reste μou alorsMoi, cependant ∫C B ∙ ds ce ne serait plus B.2πr.
Par conséquent, l'utilité de la loi d'Ampère pour déterminer le champ magnétique réside dans le choix de distributions à symétrie élevée, de sorte que l'intégrale soit facile à évaluer. Les chemins circulaires et rectilignes répondent à cette exigence.
Exercices résolus
- Exercice 1
Considérons les courbes a, b, c et d illustrées à la figure 3. Elles impliquent trois courants, deux quittant le plan, symbolisés par un point ( . ), dont les intensités sont 1 A et 5 A, et un courant qui entre dans le plan, qui est désigné par une croix et dont la magnitude est 2 A.
Trouvez le courant entouré par chaque courbe.
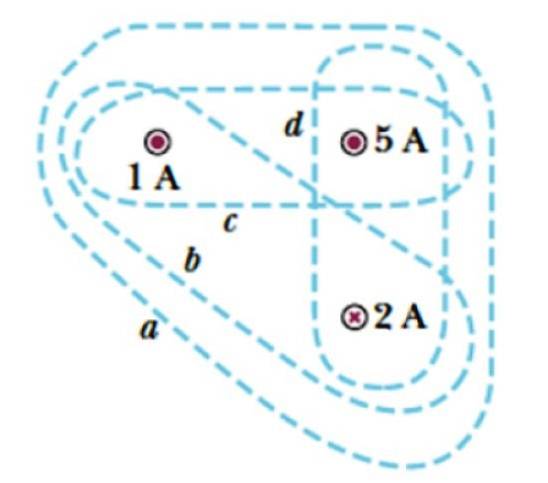
Solution
Les courants sortant du papier reçoivent un signe +. Selon ce:
Courbe a
Il renferme les trois courants, donc le courant enfermé est + 1 A + 5 A - 2 A = 4 A.
Courbe b
Seuls les courants de 1 A et - 2 A se trouvent dans cette courbe, donc le courant enfermé est de - 2 A.
Courbe c
Il renferme les courants sortants 1A et 5 A, donc le courant bloqué est de 6 A.
Incurvé
Les courants à l'intérieur sont de +5 A et - 2 A, il contient donc un courant net de 3 A.
- Exercice 2
Calculez l'amplitude du champ magnétique produit par un très long fil droit, en un point situé à 1 mètre de celui-ci, si le fil transporte un courant de 1 A.
Solution
Selon la loi d'Ampère, le champ du fil est donné par:
B = μou alorsI / 2πr = (4π x 10-7 x 1 / 2π x 1) T = 2 x 10-7 T.
Les références
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Electromagnétisme. Edité par Douglas Figueroa (USB).
- Knight, R. 2017. Physique pour les scientifiques et l'ingénierie: une approche stratégique. Pearson.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 2.
- Serway, R. 2009. Physique universitaire. Apprentissage Cengage.
- Tipler, P. (2006) Physique pour la science et la technologie. 5e éd. Volume 2. Éditorial Reverté.



Personne n'a encore commenté ce post.