La Loi de Beer-Lambert (Beer-Bouguer) est celui qui relie l'absorption du rayonnement électromagnétique d'une ou plusieurs espèces chimiques, avec sa concentration et la distance parcourue par la lumière dans les interactions particule-photon. Cette loi réunit deux lois en une.
La loi de Bouguer (bien que la reconnaissance soit davantage tombée sur Heinrich Lambert), établit qu'un échantillon absorbera plus de rayonnement lorsque les dimensions du milieu ou du matériau absorbant sont plus grandes; plus précisément, son épaisseur, qui est la distance l que la lumière se déplace en entrant et en sortant.
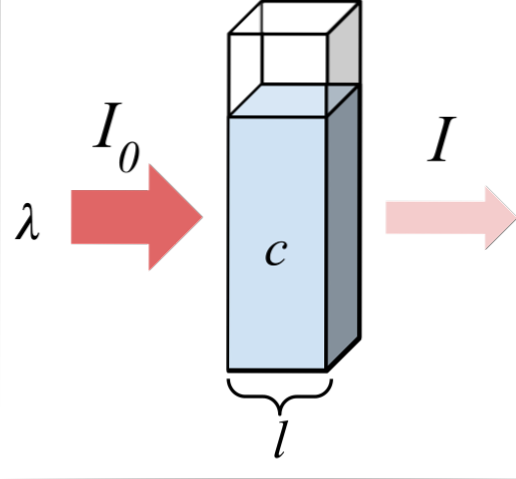
L'image du haut montre l'absorption du rayonnement monochromatique; c'est-à-dire constitué d'une seule longueur d'onde, λ. Le milieu absorbant se trouve à l'intérieur d'une cellule optique dont l'épaisseur est l, et contient des espèces chimiques avec une concentration c.
Le faisceau lumineux a une intensité initiale et finale, désignée par les symboles I0 et moi, respectivement. Notez qu'après avoir interagi avec le milieu absorbant, I est inférieur à I0, ce qui montre qu'il y a eu absorption de rayonnement. Plus ils sont âgés c Oui l, plus petit serai-je par rapport à moi0; c'est-à-dire qu'il y aura plus d'absorption et moins transmission.
Index des articles
L'image ci-dessus englobe parfaitement cette loi. L'absorption du rayonnement dans un échantillon augmente ou diminue de façon exponentielle en fonction de c ou alors l. Afin de comprendre pleinement et facilement la loi, il est nécessaire de contourner ses aspects mathématiques.
Comme je viens de le mentionner, je0 et I sont les intensités du faisceau lumineux monochromatique avant et après la lumière, respectivement. Certains textes préfèrent utiliser les symboles P0 et P, qui se réfèrent à l'énergie du rayonnement et non à son intensité. Ici, l'explication sera poursuivie en utilisant les intensités.
Pour linéariser l'équation de cette loi, il faut appliquer le logarithme, généralement la base 10:
Journal (je0/ I) = εlc
Le terme (je0/ I) indique dans quelle mesure l'intensité du produit de rayonnement d'absorption diminue. La loi de Lambert ne considère que l (εl), tandis que la loi de Beer ignore l, mais place c à la place (εc). L'équation supérieure est l'union des deux lois, et est donc l'expression mathématique générale de la loi de Beer-Lambert.
L'absorbance est définie par le terme Log (I0/ JE). Ainsi, l'équation s'exprime comme suit:
A = εlc
Où ε est le coefficient d'extinction ou l'absorbance molaire, qui est une constante à une longueur d'onde donnée.
Notez que si l'épaisseur du milieu absorbant est maintenue constante, comme ε, l'absorbance A dépendra uniquement de la concentration c, d'espèces absorbantes. C'est aussi une équation linéaire, y = mx, où Oui est A, et X c'est c.
À mesure que l'absorbance augmente, la transmittance diminue; c'est-à-dire combien de rayonnement parvient à être transmis après absorption. Ils sont donc inverses. Oui je0/ I indique le degré d'absorption, I / I0 équivaut à la transmittance. Sachant ceci:
Je / je0 = T
(JE0/ I) = 1 / T
Journal (je0/ I) = Journal (1 / T)
Mais, connectez-vous (je0/ I) est également égal à l'absorbance. La relation entre A et T est donc:
A = Journal (1 / T)
Et en appliquant les propriétés des logarithmes et en sachant que Log1 est égal à 0:
A = -LogT
Les transferts sont généralement exprimés en pourcentages:
% T = I / I0∙ 100
Comme indiqué précédemment, les équations correspondent à une fonction linéaire; par conséquent, on s'attend à ce que lors de leur représentation graphique, ils donnent une ligne.
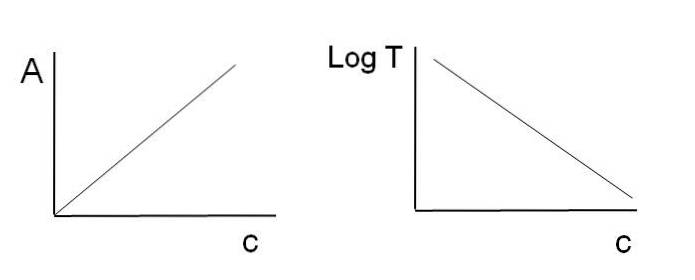
Notez qu'à gauche de l'image ci-dessus se trouve la ligne obtenue en représentant graphiquement A contre c, et à droite la ligne correspondant au graphique de LogT contre c. L'un a une pente positive et l'autre négative; plus l'absorbance est élevée, plus la transmittance est faible.
Grâce à cette linéarité, la concentration des espèces chimiques absorbantes (chromophores) peut être déterminée si l'on sait combien de rayonnement ils absorbent (A), ou combien de rayonnement est transmis (LogT). Lorsque cette linéarité n'est pas observée, on dit qu'il fait face à une déviation, positive ou négative, de la loi de Beer-Lambert.
De manière générale, certaines des applications les plus importantes de cette loi sont mentionnées ci-dessous:
-Si une espèce chimique présente une couleur, c'est un candidat exemplaire à analyser par des techniques colorimétriques. Celles-ci sont basées sur la loi de Beer-Lambert, et permettent de déterminer la concentration des analytes en fonction des absorbances obtenues avec un spectrophotomètre..
-Il permet la construction de courbes d'étalonnage, avec lesquelles, en tenant compte de l'effet matriciel de l'échantillon, la concentration de l'espèce d'intérêt est déterminée.
-Il est largement utilisé pour analyser les protéines, car plusieurs acides aminés ont des absorptions importantes dans la région ultraviolette du spectre électromagnétique..
-Les réactions chimiques ou les phénomènes moléculaires qui impliquent un changement de couleur peuvent être analysés en utilisant des valeurs d'absorbance à une ou plusieurs longueurs d'onde..
-En utilisant une analyse multivariée, des mélanges complexes de chromophores peuvent être analysés. De cette manière, la concentration de tous les analytes peut être déterminée, et également, les mélanges peuvent être classés et différenciés les uns des autres; par exemple, exclure si deux minéraux identiques proviennent du même continent ou d'un pays spécifique.
Quelle est l'absorbance d'une solution présentant une transmittance de 30% à une longueur d'onde de 640 nm??
Pour le résoudre, il suffit d'aller aux définitions d'absorbance et de transmittance.
% T = 30
T = (30/100) = 0,3
Et sachant que A = -LogT, le calcul est simple:
A = -Log 0,3 = 0,5228
Notez qu'il manque d'unités.
Si la solution de l'exercice précédent consiste en une espèce W dont la concentration est de 2,30 ∙ 10-4 M, et en supposant que la cellule a une épaisseur de 2 cm: quelle doit être sa concentration pour obtenir une transmittance de 8%??
Il pourrait être résolu directement avec cette équation:
-LogT = εlc
Mais, la valeur de ε est inconnue. Par conséquent, il doit être calculé avec les données précédentes, et on suppose qu'il reste constant sur une large gamme de concentrations:
ε = -LogT / lc
= (-Log 0,3) / (2 cm x 2,3 ∙ 10-4 M)
= 1136,52 millions-1∙ cm-1
Et maintenant, vous pouvez procéder au calcul avec% T = 8:
c = -LogT / εl
= (-Log 0,08) / (1136,52 M-1∙ cm-1 x 2 cm)
= 4,82 ∙ 10-4 M
Ensuite, il suffit que l'espèce W double sa concentration (4,82 / 2,3) pour réduire son pourcentage de transmittance de 30% à 8%..
Personne n'a encore commenté ce post.