
Explication de la loi de Coulomb, formule et unités, exercices, expériences
La Loi de Coulomb c'est la loi physique qui régit l'interaction entre les objets chargés électriquement. Il a été énoncé par le scientifique français Charles Augustin de Coulomb (1736-1806), grâce aux résultats de ses expériences utilisant la balance de torsion.
En 1785, Coulomb a expérimenté d'innombrables fois avec de petites sphères chargées électriquement, par exemple en rapprochant ou en éloignant deux sphères, en faisant varier l'amplitude de leur charge et aussi leur signe. Observez et enregistrez toujours attentivement chaque réponse.
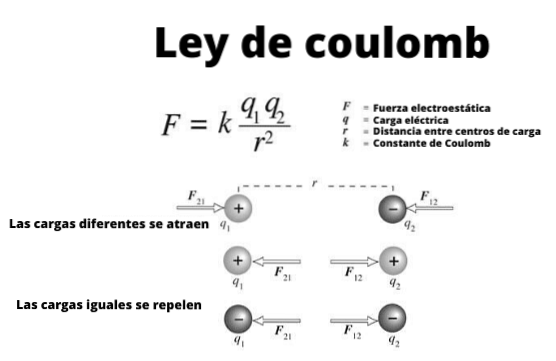
Ces petites sphères peuvent être considérées comme charges ponctuelles, c'est-à-dire des objets dont les dimensions sont insignifiantes. Et ils remplissent, comme on le sait depuis l'époque des anciens Grecs, que les charges du même signe repoussent et celles d'un signe différent s'attirent..

Dans cet esprit, Charles Coulomb a constaté ce qui suit:
-La force attractive ou répulsive entre deux charges ponctuelles est directement proportionnelle au produit de l'amplitude des charges.
-Cette force est toujours dirigée le long de la ligne qui rejoint les charges.
-Enfin, l'amplitude de la force est inversement proportionnelle au carré de la distance entre les charges.
Index des articles
- 1 Formule et unités de la loi de Coulomb
- 2 Comment appliquer la loi de Coulomb
- 3 exercices résolus
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 4 expériences
- 5 Références
Formule et unités de la loi de Coulomb
Grâce à ces observations, Coulomb a conclu que la magnitude de la force F entre deux charges ponctuelles quelle1 Oui quelledeux, séparé une distance r, est mathématiquement donnée comme:

Puisque la force est une grandeur vectorielle, pour l'exprimer complètement, un vecteur unitaire est défini r dans le sens de la ligne joignant les charges (un vecteur unitaire a une magnitude égale à 1).
De plus, la constante de proportionnalité nécessaire pour transformer l'expression précédente en égalité est appelée ket ou simplement k: le constante électrostatique ou alors Constante de Coulomb.
Enfin, la loi de Coulomb est établie pour les charges ponctuelles, données par:

La force, comme toujours dans le Système international d'unités, vient en newton (N). Concernant les charges, l'unité s'appelle coulomb (C) en l'honneur de Charles Coulomb et enfin la distance r est en mètres (m).
En regardant de près l'équation ci-dessus, il est clair que la constante électrostatique doit avoir des unités de N.mdeux / Cdeux, pour obtenir des newtons en conséquence. La valeur de la constante a été déterminée expérimentalement comme:
ket = 8,89 x 10 9 N.mdeux / Cdeux ≈ 9 x 10 9 N.mdeux / Cdeux
La figure 1 illustre l'interaction entre deux charges électriques: lorsqu'elles sont de même signe elles repoussent, sinon elles attirent.
Notez que la loi de Coulomb est conforme à la troisième loi de Newton ou loi d'action et de réaction, donc les grandeurs de F1 Oui Fdeux ils sont les mêmes, la direction est la même, mais les sens sont opposés.
Comment appliquer la loi de Coulomb
Pour résoudre les problèmes d'interactions entre charges électriques, il faut prendre en compte les éléments suivants:
- L'équation s'applique exclusivement dans le cas de charges ponctuelles, c'est-à-dire d'objets chargés électriquement mais de très petites dimensions. Si les objets chargés ont des dimensions mesurables, il est nécessaire de les diviser en très petites charges puis d'ajouter les contributions de chacune de ces charges, pour lesquelles un calcul intégral est nécessaire..
- La force électrique est une quantité vectorielle. S'il y a plus de deux charges en interaction, la force nette sur la charge qje est donné par le principe de superposition:
Frapporter = Fi1 + Fi2 + Fi3 + Fi4 +… = ∑ Fij
Où l'indice j est égal à 1, 2, 3, 4 ... et représente chacune des charges restantes.
- Vous devez toujours être cohérent avec les unités. Le plus fréquent est de travailler avec la constante électrostatique en unités SI, alors il faut s'assurer que les charges sont en coulombs et les distances en mètres.
- Enfin, l'équation s'applique lorsque les charges sont en équilibre statique.
Exercices résolus
- Exercice 1
Dans la figure suivante, il y a deux charges ponctuelles + q et + 2q. Une troisième charge ponctuelle -q est placée en P. Il est demandé de trouver la force électrique sur cette charge due à la présence des autres.

Solution
La première chose à faire est d'établir un système de référence approprié, qui dans ce cas est l'axe horizontal ou l'axe des x. L'origine d'un tel système peut être n'importe où, mais pour plus de commodité, il sera placé en P, comme le montre la figure 4a:
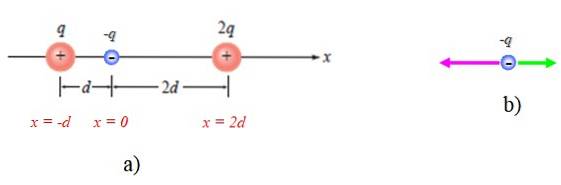
Un diagramme des forces sur -q est également montré, en tenant compte du fait qu'il est attiré par les deux autres (figure 4b).
Appelons F1 les forces exercées par la charge q sur la charge -q, sont dirigées selon l'axe des x et pointent dans le sens négatif, donc:

De manière analogue, il est calculé Fdeux:

Notez que l'ampleur de Fdeux est la moitié de celle de F1, bien que la charge soit double. Pour trouver la force nette, enfin ils sont ajoutés de manière vectorielle F1 Oui Fdeux:
Frapporter = (-k + k / 2). (qdeux / rédeux) (X) N = - (k / 2). (Qdeux / rédeux) (X) N
- Exercice 2
Deux billes de polystyrène de masse égale m = 9,0 x 10-8 kg ont la même charge positive Q et sont suspendus par un fil de soie de longueur L = 0,98 m. Les sphères sont séparées par une distance de d = 2 cm. Calculez la valeur de Q.
Solution
La situation de la déclaration est décrite dans la figure 5a.

Nous choisissons l'une des sphères et y dessinons le diagramme du corps isolé, qui comprend trois forces: le poids W, tension dans la corde T et répulsion électrostatique F, comme il apparaît sur la figure 5b. Et maintenant les étapes:
Étape 1
La valeur de θ / 2 est calculée avec le triangle de la figure 5c:
θ / 2 = arcsen (1 x 10-deux/0,98) = 0,585º
Étape 2
Ensuite, nous devons appliquer la deuxième loi de Newton et la fixer à 0, car les charges sont en équilibre statique. Surtout, la tension T est incliné et comporte deux composants:
∑FX = -T.sin θ + F = 0
∑FOui = T.cos θ - W = 0
Étape 3
Nous résolvons pour la magnitude de la contrainte de la dernière équation:
T = W / cos θ = mg / cos θ
Étape 4
Cette valeur est remplacée dans la première équation pour trouver la magnitude de F:
F = T sin θ = mg (sin θ / cos θ) = mg. tg θ
Étape 5
Puisque F = k Qdeux / rédeux, efface Q:

Q = 2 × 10-Onze C.
Expériences
La vérification de la loi de Coulomb est facile en utilisant une balance de torsion similaire à celle utilisée par Coulomb dans son laboratoire..
Il y a deux petites sphères de sureau, dont l'une, celle au centre de la balance, est suspendue par un fil. L'expérience consiste à toucher les sphères de sureau déchargées avec une autre sphère métallique chargée de charge Q.

Immédiatement, la charge est répartie également entre les deux sphères de sureau, mais ensuite, comme ce sont des charges du même signe, elles se repoussent. Une force agit sur la sphère suspendue qui provoque la torsion du fil auquel elle est suspendue et s'éloigne immédiatement de la sphère fixe.
On voit alors qu'il oscille plusieurs fois jusqu'à ce qu'il atteigne l'équilibre. Ensuite, la torsion de la tige ou du fil qui la maintient est équilibrée par la force de répulsion électrostatique.
Si à l'origine les sphères étaient à 0º, maintenant la sphère mobile aura tourné d'un angle θ. Autour de l'échelle, il y a un ruban gradué en degrés pour mesurer cet angle. En déterminant au préalable la constante de torsion, la force de répulsion et la valeur de la charge acquise par les sphères de sureau sont facilement calculées.
Les références
- Figueroa, D. 2005. Série: Physique pour les sciences et l'ingénierie. Volume 5. Électrostatique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. Deuxième édition. Mcgraw Hill.
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Salle des Prentices Ed.
- Resnick, R. 1999. Physique. Volume 2. 3e éd. En espagnol. Compañía Editorial Continental S.A. par C.V.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 2.


Personne n'a encore commenté ce post.