Bloc d'éléments d'algèbre, exemples, exercices résolus

le algèbre de bloc fait référence à l'ensemble des opérations exécutées via des blocs. Ces éléments et quelques autres servent à représenter schématiquement un système et à visualiser facilement sa réponse à une entrée donnée..

En général, un système contient divers éléments électriques, électroniques et électromécaniques, et chacun d'eux, avec sa fonction et sa position respectives dans le système, ainsi que la manière dont ils sont liés, est décrit par des blocs fonctionnels..

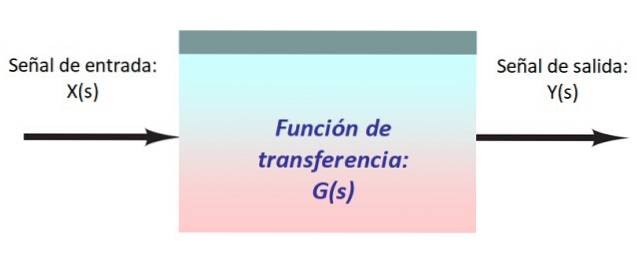
Dans la figure ci-dessus, il y a un système très simple, composé d'un signal d'entrée X (s), qui entre dans le bloc avec la fonction de transfert G (s) qui le modifie et produit la sortie Y (s).

Il est pratique de représenter les signaux et leur chemin à travers le système au moyen de flèches qui entrent et sortent de chaque bloc. Habituellement, le flux de signal est dirigé de gauche à droite.

L'avantage de ce type de schéma est l'aide visuelle qu'il fournit pour comprendre le système, même s'il ne s'agit pas d'une représentation physique du système. En fait, le schéma bloc n'est pas unique, car selon le point de vue, plusieurs schémas d'un même système peuvent même être dessinés..

Il peut également arriver que le même diagramme serve plusieurs systèmes qui ne sont pas nécessairement liés les uns aux autres, à condition qu'il décrit adéquatement leur comportement. Il existe différents systèmes dont la réponse est similaire à bien des égards, par exemple un circuit LC (inductance-condensateur) et un système masse-ressort..

Index des articles

• 1 Qu'est-ce qu'un diagramme?
• 2 Éléments du diagramme
  • 2.1 Le signal
  • 2.2 Le bloc
  • 2.3 Point de somme
  • 2.4 Point de branchement
• 3 Exemples de règles d'algèbre de bloc
  • 3.1 Blocs en cascade
  • 3.2 Blocs en parallèle
  • 3.3 Déplacer un additionneur vers la gauche
  • 3.4 Déplacer un additionneur vers la droite
  • 3.5 Déplacement d'un point de branchement de gauche à droite
  • 3.6 Déplacer un point de branchement de droite à gauche
  • 3.7 Système de rétroaction
  • 3.8 Système avec retour et transducteur
• 4 exercices résolus
  • 4.1 Exercice 1
  • 4.2 Exercice 2
• 5 Références

Qu'est-ce qu'un schéma de principe?

Les systèmes sont généralement plus compliqués que celui de la figure 1, mais l'algèbre par blocs fournit une série de règles simples pour manipuler le schéma du système et le réduire à sa version la plus simple..

Comme expliqué au début, le diagramme utilise des blocs, des flèches et des cercles pour établir la relation entre chaque composant du système et le flux de signaux qui le traverse..

L'algèbre par blocs vous permet de comparer deux signaux ou plus en les ajoutant, en soustrayant et en les multipliant, ainsi qu'en analysant la contribution que chaque composant apporte au système.

Grâce à cela, il est possible de réduire l'ensemble du système à un seul signal d'entrée, une seule fonction de transfert qui décrit pleinement l'action du système et la sortie correspondante..

Éléments de schéma de principe

Les éléments du diagramme sont les suivants:

Le signal

Les signaux sont de nature très variée, par exemple il est courant qu'il s'agisse d'un courant électrique ou d'une tension, mais il peut s'agir de lumière, de son et plus encore. L'important est qu'il contienne des informations sur un certain système.

Le signal est noté avec une majuscule s'il est fonction de la variable s de la transformée de Laplace: X (s) (voir figure 1) ou en minuscules si elle est fonction du temps t, comme x (t).

Dans le schéma synoptique, le signal d'entrée est représenté par une flèche dirigée vers le bloc, tandis que le signal de sortie, noté Y (s) ou y (t), est indiqué par une flèche sortante.

Les signaux d'entrée et de sortie sont uniques et la direction dans laquelle les informations circulent est déterminée par la direction de la flèche. Et l'algèbre est la même pour l'une ou l'autre des deux variables.

Le bloc

Le bloc est représenté par un carré ou un rectangle (voir figure 1) et peut être utilisé pour effectuer des opérations ou implémenter la fonction de transfert, qui est généralement désignée par la lettre majuscule G. Cette fonction est un modèle mathématique utilisant qui décrit la réponse offert par le système à un signal d'entrée.

La fonction de transfert peut être exprimée en termes de temps t comme G (t) ou la variable s comme G (s).

Lorsque le signal d'entrée X (s) atteint le bloc, il est multiplié par la fonction de transfert et transformé en signal de sortie Y (s). Mathématiquement, il est exprimé comme ceci:

Y (s) = X (s) .G (s)

De manière équivalente, la fonction de transfert est le rapport entre la transformée de Laplace du signal de sortie et la transformée de Laplace du signal d'entrée, à condition que les conditions initiales du système soient nulles:

G (s) = Y (s) / X (s)

Point de somme

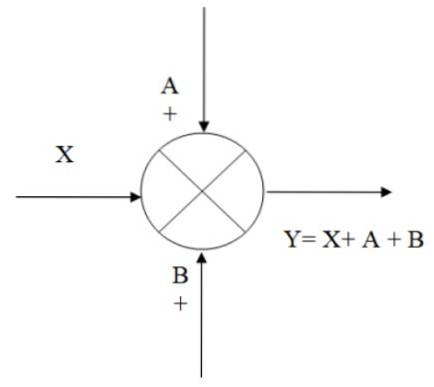
Le point d'addition, ou additionneur, est symbolisé par un cercle avec une croix à l'intérieur. Il est utilisé pour combiner, par addition et soustraction, deux ou plusieurs signaux. A la fin de la flèche qui symbolise le signe, un signe + est placé directement si ledit signe est ajouté ou un signe - s'il est soustrait..

Dans la figure suivante, il y a un exemple du fonctionnement de l'additionneur: nous avons le signal d'entrée X, auquel s'ajoutent les signaux A et B, obtenant ainsi la sortie Y, qui est algébriquement équivalente à:

Y = X + A + B

Point de branchement

Il s'appelle aussi point de bifurcation. Dans celui-ci, le signal qui sort d'un bloc est distribué à d'autres blocs ou à un additionneur. Il est représenté par un point placé sur la flèche du signal et une autre flèche en sort qui redirige le signal vers une autre partie.

Exemples de règles d'algèbre de bloc

Comme expliqué précédemment, l'idée est d'exprimer le système à l'aide du diagramme et de le réduire pour trouver la fonction de transfert qui le décrit. Voici les règles d'algèbre de bloc pour simplifier les diagrammes:

Blocs en cascade

Lorsque vous avez un signal qui passe successivement à travers les blocs G₁, g_deux, g₃..., se réduit à un seul bloc dont la fonction de transfert est le produit de G₁, g_deux, g₃...

Dans l'exemple suivant, le signal X (s) entre dans le premier bloc et sa sortie est:

Oui₁(s) = X (s) .G₁(s)

Tourner Y₁(s) entrer dans le bloc G_deux(s), dont la sortie est:

Oui_deux(s) = X (s) .G₁(s). g_deux(s)

La procédure est valable pour n blocs en cascade:

Oui_n (s) = X (s). g₁(s) .G_deux(s) ... G_n(s)

Blocs parallèles

Dans le schéma de gauche, le signal X (s) se branche pour entrer dans les blocs G₁(s) et G_deux(s):

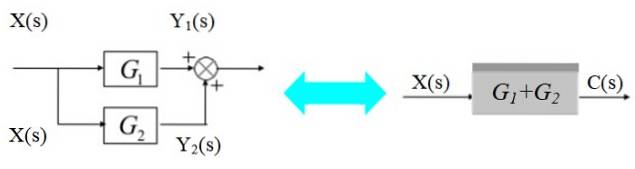
Les signaux de sortie respectifs sont:

Oui₁(s) = X (s) .G₁(s)

Oui_deux(s) = X (s) .G_deux(s)

Ces signaux sont additionnés pour obtenir:

C (s) = Y₁(s) + Y_deux(s) = X (s). [G₁(s) + G_deux(s)]

Comme indiqué dans le diagramme à droite.

Déplacer un additionneur vers la gauche

Un additionneur peut être déplacé vers la gauche du bloc comme suit:

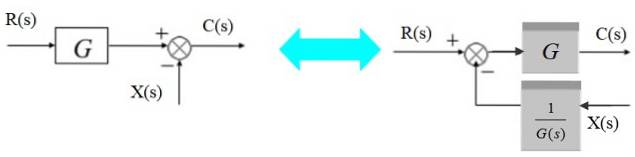
Sur la gauche, le signal de sortie est:

C (s) = R (s). G (s) - X (s)

De manière équivalente à droite:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Déplacer un additionneur vers la droite

L'additionneur peut être déplacé vers la droite du bloc comme ceci:

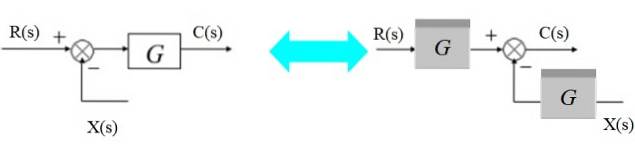
À gauche, nous avons: [R (s) - X (s)]. G (s) = C (s)

Et à droite:

R (s). G (s) - X (s). G (s) = C (s)

Déplacer un point de branchement de gauche à droite

Pour déplacer le point de branchement de gauche à droite du bloc, il suffit d'observer que la sortie C (s) vers la droite est le produit X (s) .G (s). Puisque vous voulez le convertir à nouveau en X (s), multipliez par l'inverse de G (s).

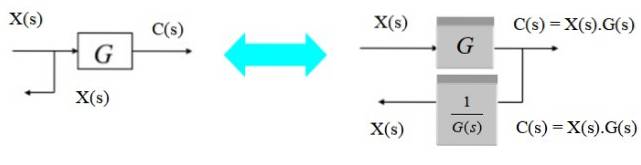
Déplacer un point de branchement de droite à gauche

Alternativement, le point de branchement peut être déplacé de droite à gauche comme suit:

Puisque à la sortie de la branche on veut obtenir C (s), il suffit d'insérer un nouveau bloc G (s) à un point de branche à gauche du bloc d'origine.

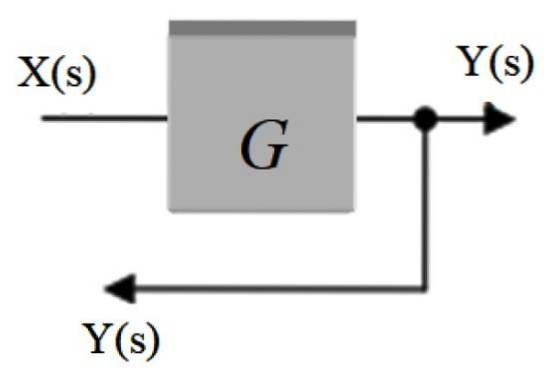
Système de rétroaction

Dans le système suivant, le signal de sortie C (s) est renvoyé par l'additionneur à gauche:

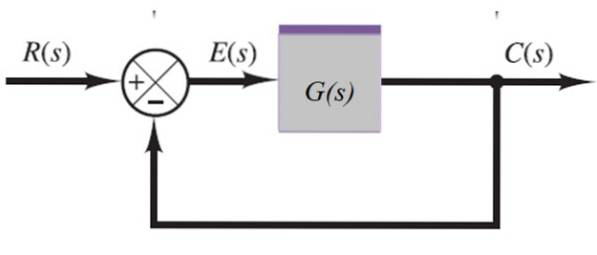
C (s) = E (s) .G (s)

Mais:

E (s) = R (s) -C (s)

En remplaçant cette expression dans l'équation précédente, il reste: C (s) = [R (s) -C (s)]. G (s), à partir de laquelle C (s) peut être résolu:

C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Ou bien:

C (s) / R (s) = G (s) / [1 + G (s)]

Sous forme graphique, après simplification il reste:

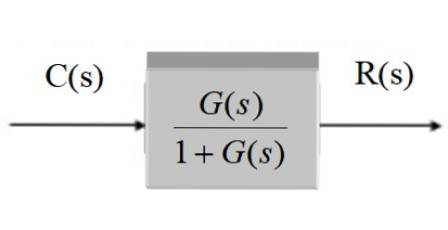
Système avec retour et transducteur

Le transducteur se compose de la fonction de transfert H (s):

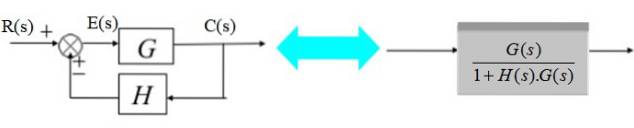
Dans le schéma de droite, le signal de sortie C (s) est:

C (s) = E (s). G (s) avec E (s) = R (s) - C (s). H (s)

Ensuite:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Par conséquent, C (s) peut être résolu par:

C (s) = G (s) .R (s) / [1+ H (s) .G (s)]

Et la fonction de transfert sera:

G (s) / [1+ H (s) .G (s)]

Comme le montre le diagramme simplifié à droite.

Exercices résolus

Exercice 1

Recherchez la fonction de transfert du système suivant:

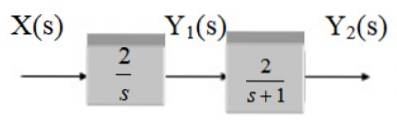
Solution

Il traite deux blocs en cascade, donc la fonction de transfert est le produit des fonctions G₁ et G_deux.

Il faut que:

g₁ = 2 / s

g_deux = 2 / (s + 1)

La fonction de transfert recherchée est donc:

G (s) = 4 / [s (s + 1)]

Exercice 2

Réduisez le système suivant:

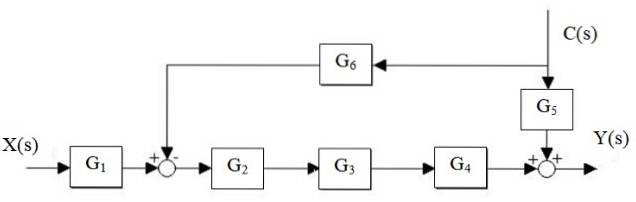
Solution

Tout d'abord, la cascade G est réduite_deux, g₃ et G_4, et le parallèle G est séparé₅ et G₆:

Puis l'additionneur à gauche du bloc G_deux ⋅G₃ ⋅ G₄ se déplace vers la droite:

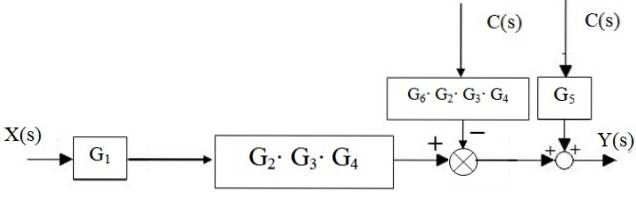
Les additionneurs de droite sont réduits à un seul, ainsi que les blocs en cascade:

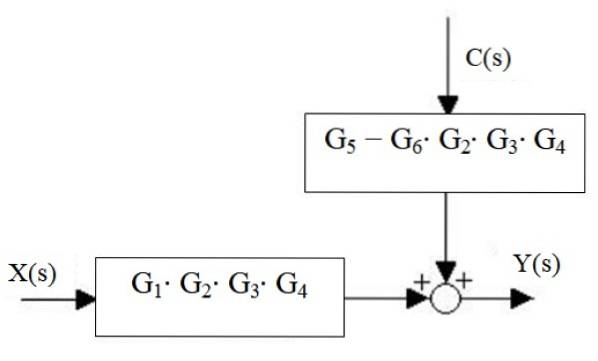
Enfin, la sortie du système est:

Y (s) = X (s) ⋅G₁⋅ G_deux ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - g₆ ⋅ G_deux ⋅G₃ ⋅ G₄]

Les références

1. Alaydi, J. Schéma fonctionnel du système de contrôle. Récupéré de: site.iugaza.edu.ps.
2. Bolton, W. 2006. Ingénierie de contrôle. 2ème. Édition. Alpha Oméga.
3. Cwalinsky, J. Introduction à l'algèbre des blocs système. Récupéré de: cedengineering.com.
4. Dademuchconnection. Diagramme de blocs. Récupéré de: dademuch.com.
5. Ogata, K. 2010. Ingénierie de contrôle moderne. 5ème. Édition. Pearson.