
Calcul de matrice inverse et exercice résolu
La Matrice inverse d'une matrice donnée, c'est la matrice multipliée par les résultats originaux dans la matrice identité. La matrice inverse est utile pour résoudre des systèmes d'équations linéaires, d'où l'importance de savoir la calculer.
Les matrices sont très utiles en physique, en ingénierie et en mathématiques, car elles constituent un outil compact pour résoudre des problèmes complexes. L'utilité des matrices est renforcée lorsqu'elles sont inversibles et leur inverse est également connu.
Dans les domaines du traitement graphique, du Big Data, du Data Mining, du Machine Learning et autres, des algorithmes efficaces et rapides sont utilisés pour évaluer la matrice inverse de matrices nxn à très grand n, de l'ordre de milliers ou millions.
Pour illustrer l'utilisation de la matrice inverse dans le traitement d'un système d'équations linéaires, nous allons commencer par le cas le plus simple de tous: matrices 1 × 1.
Le cas le plus simple: une équation linéaire d'une seule variable est considérée: 2 x = 10.
L'idée est de trouver la valeur de x, mais cela se fera "matriciel".
La matrice M = (2) qui multiplie le vecteur (x) est une matrice 1 × 1 qui aboutit au vecteur (10):
M (x) = (10)
L'inverse de la matrice M est noté M-1.
La manière générale d'écrire ce "système linéaire" est:
M X = B, où X est le vecteur (x) et B est le vecteur (10).
Par définition, la matrice inverse est celle qui, multipliée par la matrice d'origine, donne la matrice d'identité I:
M-1 M = I
Dans le cas considéré, la matrice M-1 est la matrice (½), c'est-à-dire M-1 = (½) puisque M-1 M = (½) (2) = (1) = I
Pour trouver le vecteur inconnu X = (x), dans l'équation proposée, les deux membres sont multipliés par la matrice inverse:
M-1 M (x) = M-1 (dix)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
Une égalité de deux vecteurs a été atteinte, qui ne sont égaux que lorsque leurs éléments correspondants sont égaux, c'est-à-dire x = 5.
Calcul de l'inverse d'une matrice
Ce qui motive le calcul de la matrice inverse est de trouver une méthode universelle pour la résolution de systèmes linéaires comme le système 2 × 2 suivant:
x - 2 y = 3
-x + y = -2
En suivant les étapes du cas 1 × 1, étudié dans la section précédente, nous écrivons le système d'équations sous forme matricielle:
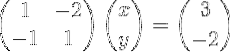
Notez que ce système est écrit en notation vectorielle compacte comme suit:
M X = B
où
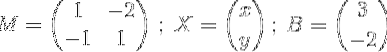
L'étape suivante consiste à trouver l'inverse de M.
Méthode 1: Utilisation de l'élimination gaussienne
La méthode d'élimination gaussienne sera appliquée. Qui consiste à faire des opérations élémentaires sur les lignes de la matrice, ces opérations sont:
- Multiplier une ligne par un nombre différent de zéro.
- Ajouter ou soustraire d'une ligne une autre ligne, ou le multiple d'une autre ligne.
- Échangez les lignes.
L'objectif est, à travers ces opérations, de convertir la matrice d'origine en matrice d'identité.
Comme cela est fait, dans la matrice M exactement les mêmes opérations sont appliquées à la matrice d'identité. Lorsqu'après plusieurs opérations sur les lignes M est transformée en matrice unitaire, alors celle qui était à l'origine l'unité sera transformée en matrice inverse de M, c'est-à-dire M-1.
1- Nous commençons le processus en écrivant la matrice M et à côté d'elle la matrice unitaire:
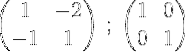
2- On ajoute les deux lignes et on met le résultat dans la deuxième ligne, de cette façon on obtient un zéro dans le premier élément de la deuxième ligne:
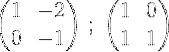
3- On multiplie la deuxième ligne par -1 pour obtenir 0 et 1 dans la deuxième ligne:
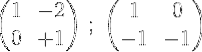
4- La première ligne est multipliée par ½:
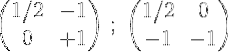
5- Le deuxième et le premier sont ajoutés et le résultat est placé dans la première ligne:
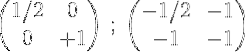
6- Pour terminer le processus, multipliez la première ligne par 2 pour obtenir la matrice d'identité dans la première ligne et la matrice inverse de la matrice d'origine M dans la seconde:
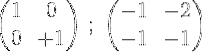
C'est-à-dire:
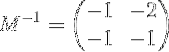
Solution système
Une fois la matrice inverse obtenue, nous procédons à la résolution du système d'équations en appliquant la matrice inverse aux deux membres de l'équation vectorielle compacte:
M-1M X = M-1B
X = M-1B
Ce qui ressemble explicitement à ceci:
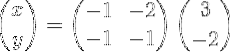
Ensuite, la multiplication matricielle est effectuée pour obtenir le vecteur X:
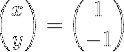
Méthode 2: utilisation de la matrice jointe
Dans cette seconde méthode, la matrice inverse est calculée à partir de la matrice adjacente de la matrice d'origine À.
Supposons une matrice A donnée par:

où allerje, j est l'élément de la ligne je et la colonne j de la matrice À.
L'adjoint de la matrice À ça s'appellera Aj (A) et ses éléments sont:
un dje, j = (-1)(i + j) ¦Ai, j¦
où Ai, j est la matrice mineure complémentaire obtenue en éliminant la ligne i et la colonne j de la matrice d'origine À. Les barres ¦ ¦ indiquent que le déterminant est calculé, c'est-à-dire ¦Ai, j¦ est le déterminant de la matrice mineure complémentaire.
Formule de matrice inverse
La formule pour trouver la matrice inverse à partir de la matrice adjacente de la matrice d'origine est la suivante:
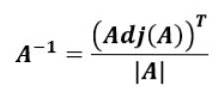
Autrement dit, la matrice inverse de À, À-1, est la transposée de l'adjoint de À divisé par le déterminant de À.
La transposition ÀTd'une matrice À est celle obtenue en échangeant des lignes contre des colonnes, c'est-à-dire que la première ligne devient la première colonne et la deuxième ligne devient la deuxième colonne et ainsi de suite jusqu'à ce que les n lignes de la matrice d'origine soient complétées.
Exercice résolu
Soit la matrice A la suivante:
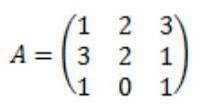
Chaque élément de la matrice adjointe de A est calculé: Adj (A)
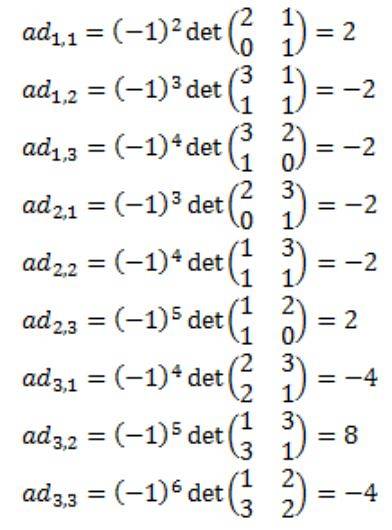
Il en résulte que la matrice adjointe de A, Adj (A) est la suivante:
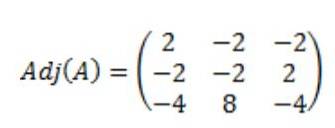
Ensuite, le déterminant de la matrice A, det (A) est calculé:
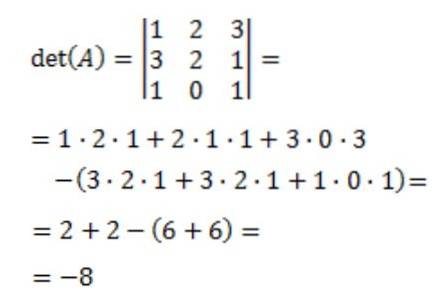
Enfin la matrice inverse de A est obtenue:
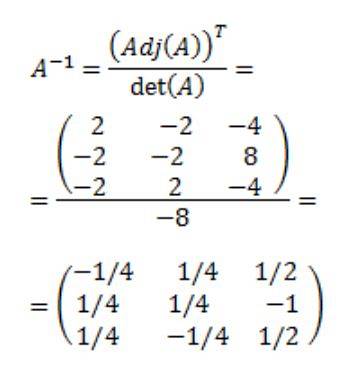
Les références
- Anthony Nicolaides (1994) Déterminants et matrices. Publication de réussite.
- Awol Assen (2013) Une étude sur le calcul des déterminants d'un 3 × 3
- Casteleiro Villalba M. (2004) Introduction à l'algèbre linéaire. Éditorial ESIC.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: Guide de survie d'un étudiant. la presse de l'Universite de Cambridge.
- Richard J. Brown (2012) 30 secondes de mathématiques: les 50 théories les plus expansionnistes en mathématiques. Ivy presse limitée.
- Matrice. Édition académique Lap Lambert.



Personne n'a encore commenté ce post.