le mouvement de rotation de la terre est celui que notre planète tourne autour du L'axe de la Terre dans une direction ouest-est et dure environ une journée, plus précisément 23 heures, 56 minutes et 3,5 secondes.
Ce mouvement, ainsi que la translation autour du soleil, sont les plus importants de la Terre. En particulier, le mouvement de rotation est très influent dans la vie quotidienne des êtres vivants, car il donne lieu à des jours et des nuits.
Par conséquent, chaque intervalle de temps a une certaine quantité d'éclairage solaire, ce que l'on appelle communément jour, et l'absence de lumière du soleil ou nuit. La rotation de la Terre entraîne également des changements de température, car le jour est une période de réchauffement, tandis que la nuit est une période de refroidissement..
Ces circonstances marquent un jalon dans tous les êtres vivants qui peuplent la planète, donnant lieu à une multitude d'adaptations en termes d'habitudes de vie. Selon elle, les entreprises ont établi les périodes d'activité et de repos selon leurs coutumes et influencées par l'environnement..
Évidemment, les zones claires et sombres changent au fur et à mesure du mouvement. En divisant 360º qui a une circonférence, entre les 24 heures auxquelles un jour est arrondi, il s'avère qu'en 1 heure la terre a tourné de 15º dans une direction ouest-est.
Par conséquent, si nous nous déplaçons vers l'ouest 15º, c'est une heure plus tôt, c'est l'inverse qui se produit si nous voyageons vers l'est.
La vitesse de rotation de la Terre sur son propre axe a été estimée à 1600 km / h à l'équateur, avec la diminution conséquente à l'approche des pôles, jusqu'à ce qu'elle s'annule juste sur l'axe de rotation..
Index des articles
La raison pour laquelle la Terre tourne autour de son axe réside dans les origines du système solaire. Peut-être que le Soleil n'a passé longtemps qu'après que la gravité a rendu possible sa naissance à partir de la matière amorphe qui peuplait l'espace. Au fur et à mesure que le Soleil se formait, il acquit la rotation fournie par le nuage primitif de matière..
Une partie de la matière qui a donné naissance à l'étoile a été compactée autour du Soleil pour créer les planètes, qui avaient également leur part du moment cinétique du nuage d'origine. De cette façon, toutes les planètes (y compris la Terre) ont leur propre mouvement de rotation dans la direction ouest-est, à l'exception de Vénus et Uranus, qui tournent dans la direction opposée..
Certains pensent qu'Uranus est entré en collision avec une autre planète de densité similaire et, en raison de l'impact, a changé son axe et sa direction de rotation. Sur Vénus, l'existence de marées gazeuses pourrait expliquer pourquoi le sens de rotation s'inversait lentement avec le temps.
Le moment cinétique est, en rotation, ce que le moment linéaire est à la translation. Pour un corps tournant autour d'un axe fixe comme la Terre, sa magnitude est donnée par:
L = Iω
Dans cette équation L est le moment cinétique (kg.mdeux/ s), je est le moment d'inertie (kg.mdeux) O w est la vitesse angulaire (radians / s).
Le moment cinétique est conservé tant qu'il n'y a pas de couple net agissant sur le système. Dans le cas de la formation du système solaire, le Soleil et la matière qui ont donné naissance aux planètes sont considérés comme un système isolé, sur lequel aucune force n'a provoqué de couple externe.
En supposant que la Terre est une sphère parfaite et se comporte comme un corps rigide et en utilisant les données fournies, son moment cinétique de rotation doit être trouvé: a) autour de son propre axe et b) dans son mouvement de translation autour du Soleil.
Données: moment d'inertie d'une sphère = Isphère = (2/5) MRdeux; masse terrestre M = 5,9721024 Kg, rayon de la Terre R = 6371 Km; distance moyenne entre la Terre et le Soleil Rm = 149,6 x 106 Km.
a) Il faut d'abord avoir le moment d'inertie de la Terre considéré comme une sphère de rayon R et de masse M.
I = (2/5) ' 5 972 1024 Kg '(6371'dix3 Km)deux = 9,7 'dix37 kg.mdeux
La vitesse angulaire est calculée comme ceci:
ω = 2π/ T
Où T est la période du mouvement, qui dans ce cas est de 24 heures = 86400 s, donc:
ω = 2π/ T = 2π/ 86400 s = 0,00007272 s-1
Le moment cinétique de la rotation autour de son propre axe est:
L = 9,7 'dix37 kg.mdeux' 0,00007272 s-1 = 7,05'dix33 kg.mdeux/ s
b) En ce qui concerne le mouvement de translation autour du Soleil, la Terre peut être considérée comme un objet ponctuel, dont le moment d'inertie est I = M.Rdeuxm
I = M.Rdeuxm= 5 972 1024 Kg'(149,6 ' dix6 × 1000 m)deux = 1,33'dix47kg.mdeux
Dans un an, il y a 365 ×24 × 86400 s = 3,1536 × dix7 s, la vitesse angulaire orbitale de la Terre est:
ω = 2π/ T = 2π/3,1536 × dix7 s = 1,99 ×dix-7 s-1
Avec ces valeurs, le moment cinétique orbital de la Terre est:
L = 1,33'dix47kg.mdeux × 1 .99 × dix-7 s-1 = 2,65 × dix40 kg.mdeux/ s
Comme mentionné ci-dessus, la succession des jours et des nuits, avec leurs changements respectifs d'heures de lumière et de température, est la conséquence la plus importante du mouvement de rotation de la Terre sur son propre axe. Cependant, son influence va un peu au-delà de ce fait décisif:
- La rotation de la Terre est étroitement liée à la forme de la planète. La Terre n'est pas une sphère parfaite comme une boule de billard. Lorsqu'il tourne, des forces se développent qui le déforment, provoquant un renflement à l'équateur et un aplatissement consécutif aux pôles..
- La déformation de la Terre donne lieu à de petites fluctuations de la valeur de l'accélération de la pesanteur g dans différents endroits. Par exemple, la valeur de g est plus grand aux pôles qu'à l'équateur.
- Le mouvement de rotation influence grandement la distribution des courants océaniques et affecte grandement les vents, en raison du fait que les masses d'air et d'eau subissent des écarts par rapport à leur trajectoire à la fois dans le sens des aiguilles d'une montre (hémisphère nord) et dans le sens des aiguilles d'une montre (hémisphère sud)..
- le fuseaux horaires, afin de réguler le passage du temps à chaque endroit, car différentes zones de la Terre sont éclairées par le soleil ou assombries.
L'effet Coriolis est une conséquence de la rotation de la Terre. Puisqu'il y a accélération dans toute rotation, la Terre n'est pas considérée comme un cadre de référence inertiel, ce qui est nécessaire pour appliquer les lois de Newton.
Dans ce cas, apparaissent les soi-disant pseudo-forces, des forces dont l'origine n'est pas physique, comme la force centrifuge subie par les passagers d'une voiture lorsqu'elle fait un virage et qu'ils sentent qu'ils sont déviés d'un côté..
Pour visualiser ses effets, considérons l'exemple suivant: il y a deux personnes A et B sur une plate-forme en rotation antihoraire, toutes deux au repos par rapport à elle. La personne A lance une balle à la personne B, mais lorsque la balle atteint l'endroit où se trouvait B, elle s'est déjà déplacée et la balle est déviée d'une certaine distance. s, passant derrière B.
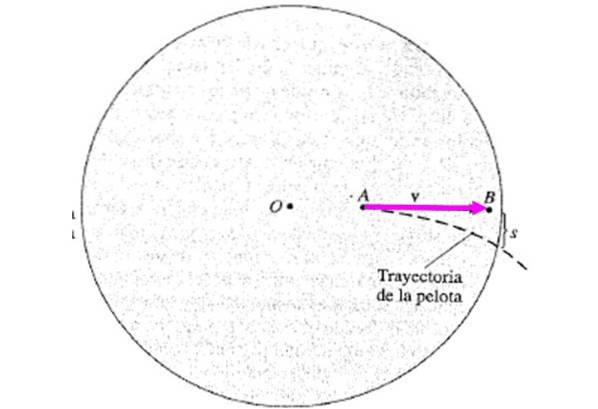
La force centrifuge n'est pas responsable dans ce cas, elle agit déjà hors du centre. C'est la force de Coriolis, dont l'effet est de dévier le ballon latéralement. Il arrive que A et B aient des vitesses ascendantes différentes, car ils sont à des distances différentes de l'axe de rotation. La vitesse de B est plus élevée et elles sont données par:
vÀ = ωRÀ ; vB = ωRB
L'accélération de Coriolis a des effets importants sur le mouvement des masses d'air, et affecte donc le climat. C'est pourquoi il est important d'en tenir compte pour étudier le mouvement des courants d'air et des courants océaniques..
Les gens peuvent également en faire l'expérience lorsqu'ils essaient de marcher sur une plate-forme rotative, comme un carrousel en mouvement..
Pour le cas représenté sur la figure précédente, supposons que la gravité ne soit pas prise en compte et que le mouvement soit visualisé à partir d'un système de référence inertiel, extérieur à la plate-forme. Dans ce cas, le mouvement ressemble à ceci:
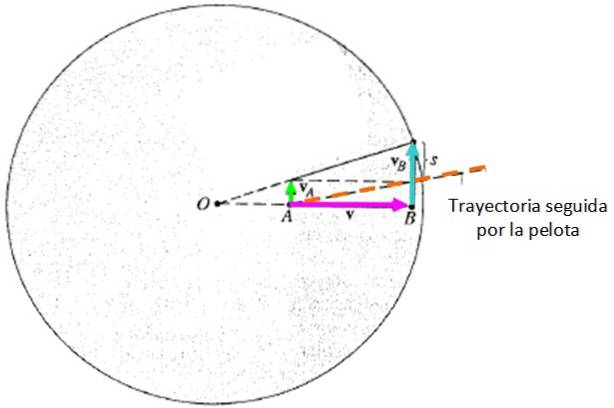
La déviation du ballon par rapport à la position initiale de la personne B est:
s = sB - sÀ = vt = (vB - vÀ) t = (ωRB - ωRÀ) t = = ω(RB - RÀ) t
Mais RB - RÀ = vt, alors:
s = ω .(Vermont). t = ωVermontdeux
C'est un mouvement avec une vitesse initiale 0 et une accélération constante:
s = ½ aCoriolis tdeux
àCoriolis = 2ω.v
Personne n'a encore commenté ce post.