
Exemples de méthodes de parallélogramme, exercices résolus
le méthode du parallélogramme est une méthode graphique pour ajouter deux vecteurs dans le plan. Il est fréquemment utilisé pour trouver la résultante de deux forces appliquées à un corps ou de deux vitesses, comme dans le cas d'un nageur qui a l'intention de traverser une rivière perpendiculairement et est dévié par le courant..
Pour construire le parallélogramme, les origines des vecteurs à ajouter, dessinés à l'échelle, doivent coïncider en un point.
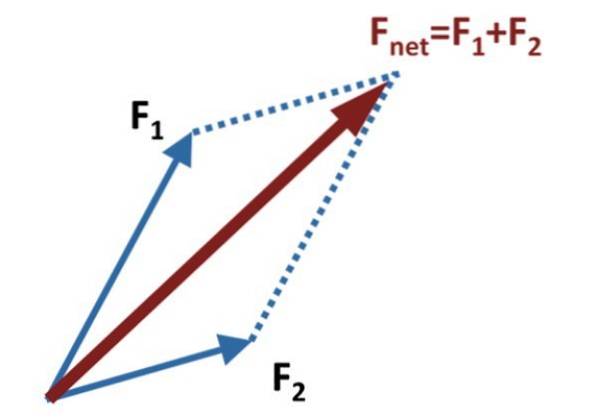
Ensuite, des lignes auxiliaires sont dessinées parallèlement à chaque vecteur, atteignant l'extrémité de l'autre, comme le montre la figure ci-dessus.
La somme ou le vecteur résultant, également appelé force nette, est le vecteur Frapporter, qui s'obtient en dessinant le vecteur qui part de l'origine commune de F1 Oui Fdeux, jusqu'au point d'intersection des lignes parallèles auxiliaires. Dans le diagramme de la figure, ceux-ci sont représentés par des lignes pointillées.
La méthode tire son nom de la figure formée avec les vecteurs addend et les lignes auxiliaires, qui est précisément un parallélogramme. La diagonale principale du parallélogramme est le vecteur somme.
Il est très important de noter que l'ordre dans lequel les vecteurs addend sont placés ne modifie en rien la somme, puisque cette opération entre vecteurs est commutative.
Index des articles
- 1 Exemple de la méthode du parallélogramme pas à pas
- 1.1 Cas particulier: somme des vecteurs perpendiculaires
- 2 exercices résolus
- 2.1 - Exercice 1
- 2.2 - Exercice 2
- 3 Références
Exemple de la méthode du parallélogramme pas à pas
L'image suivante montre les vecteurs v Oui ou alors en unités arbitraires. Le vecteur v mesure 3,61 unités et forme un angle de 56,3 ° avec l'horizontale, tandis que ou alors mesure 6,32 unités et un angle de 18,4 ° par rapport à ladite ligne de référence.
Nous allons trouver sa somme vectorielle en utilisant la méthode du parallélogramme.
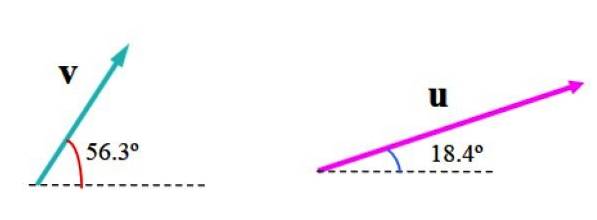
Choisissez une échelle appropriée, telle que celle illustrée dans la figure suivante, dans laquelle le plan a été divisé par une grille. La largeur du carré représente une (1) unité.
Puisque les vecteurs ne sont pas modifiés lors de la translation, ils sont positionnés de telle sorte que leurs origines coïncident avec l'origine du système de coordonnées (image à gauche).
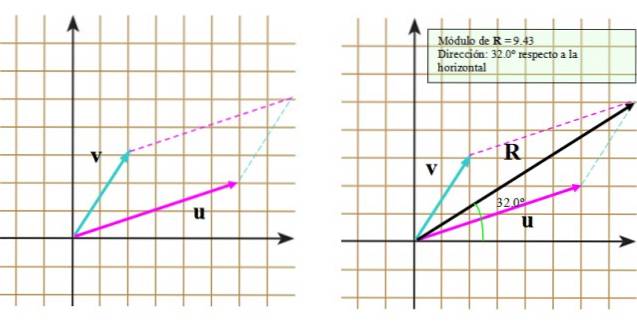
Maintenant, suivons ces étapes:
- Tracer par fin de vecteur v une ligne segmentée parallèle au vecteur ou alors.
- Répétez la procédure mais cette fois avec la fin du vecteur ou alors.
- Tracez la diagonale principale s'étendant de l'origine commune au point d'intersection des lignes segmentées.
Le résultat peut être vu dans l'image de droite, dans laquelle le vecteur résultant apparaît R.
Si nous voulons connaître l'ampleur de R, nous pouvons mesurer sa longueur et la comparer à l'échelle dont nous disposons. Et quant à sa direction, l'axe horizontal ou l'axe vertical peuvent être utilisés comme références, par exemple.
Lorsque vous utilisez l'axe horizontal ou l'axe x, l'angle qui R la forme avec ledit axe est mesurée avec le rapporteur et de cette façon nous connaissons la direction de R.
De même, l'ampleur et la direction de R peut être calculé à l'aide des théorèmes cosinus et sinusoïdal, puisque le parallélogramme formé peut être divisé en deux triangles congruents, dont les côtés sont les modules des vecteurs ou alors, v Oui R. Voir l'exemple travaillé 1.
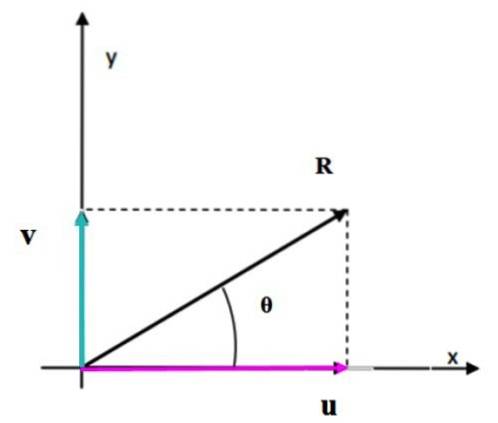
Cas particulier: somme des vecteurs perpendiculaires
Lorsque les vecteurs sont perpendiculaires les uns aux autres, la figure formée est un rectangle. Le module du vecteur résultant correspond à la longueur de la diagonale, qui peut être facilement calculée en utilisant le théorème de Pythagore.
Exercices résolus
- Exercice 1
Nous avons le vecteur v, qui mesure 3,61 unités et forme un angle de 56,3 ° avec l'horizontale et le vecteur ou alors, dont la mesure est de 6,32 unités et forme un angle de 18,4 ° (figure 2). Déterminer le module du vecteur résultant R = ou alors + v et la direction que le vecteur forme avec l'axe horizontal.
Solution
La méthode du parallélogramme est appliquée selon les étapes décrites ci-dessus, pour obtenir le vecteur R. Comme dit précédemment, si les vecteurs sont soigneusement dessinés en suivant l'échelle et en utilisant la règle et le rapporteur, la magnitude et la direction de R sont mesurés directement sur le dessin.
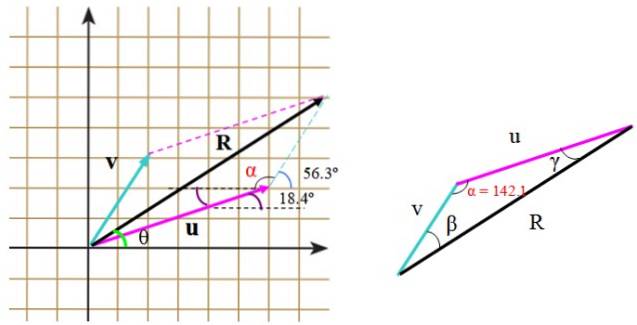
Ils peuvent également être calculés directement, à l'aide de la trigonométrie et des propriétés des angles. Lorsque le triangle formé n'est pas droit, comme dans ce cas, le théorème du cosinus est appliqué pour trouver le côté manquant.
Dans le triangle de droite, les côtés mesurent u, v et R. Pour appliquer le théorème du cosinus il faut connaître l'angle entre v Oui ou alors, que nous pouvons trouver à l'aide de la grille, en positionnant de manière appropriée les angles fournis par la déclaration.
Cet angle est α et est composé de:
α = (90-56,3 °) + 90 ° + 18,4 ° = 142,1 °
Selon le théorème du cosinus:
Rdeux = vdeux + ou alorsdeux - 2u⋅v⋅cos α = 3,61deux + 6,32deux - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 unités.
Enfin, l'angle entre R et l'axe horizontal est θ = 18,4 º + γ. L'angle γ peut être trouvé en utilisant le théorème du sinus:
sin α / R = sin γ / u
Donc:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6 °
θ = 18,4 ° + 13,6 ° = 32 °
- Exercice 2
Un nageur s'apprête à traverser une rivière en nageant perpendiculairement au courant avec une vitesse constante de 2,0 m / s. Le nageur part de A, mais finit en B, un point en aval, en raison du courant qui l'a détourné.
Si la vitesse du courant est de 0,8 m / s et que toutes les vitesses sont supposées constantes, trouvez la vitesse du nageur vue par un observateur debout sur le rivage..
Solution
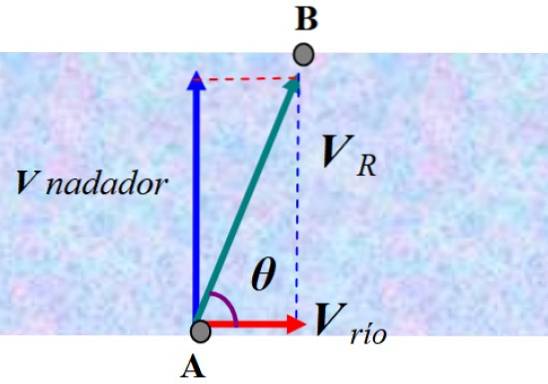
Un observateur debout sur le rivage verrait comment le nageur est dévié en fonction de la vitesse résultante VR. Pour trouver la réponse, il faut ajouter de manière vectorielle la vitesse du nageur par rapport à l'eau et la vitesse du courant, que nous appelons V fleuve:
V R = V nageur + V fleuve
Dans la figure, qui n'est pas à l'échelle, les vecteurs ont été ajoutés pour obtenir V R. Dans ce cas, le théorème de Pythagore peut être appliqué pour obtenir sa magnitude:
VRdeux = 2,0deux + 0,8deux = 4,64
VR = 2,15 m / s
La direction dans laquelle le nageur s'écarte de la direction perpendiculaire est facilement calculée, en notant que:
θ = arcg (2 / 0,8) = 68,2 °
Ensuite, le nageur s'écarte de 90 ° - 68,2 ° = 27,2 ° de sa direction d'origine.
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill.
- Bedford, 2000. A. Mécanique du génie: statique. Addison Wesley.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 1. Cinématique. Edité par Douglas Figueroa (USB).
- Giambattista, A. 2010. Physique. 2ème. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 1.



Personne n'a encore commenté ce post.