
Formules orthoèdres, aire, volume, diagonale, exemples
le orthoèdre Il s'agit d'une figure géométrique volumétrique ou tridimensionnelle qui se caractérise par avoir six faces rectangulaires, de sorte que les faces opposées sont dans des plans parallèles et sont des rectangles identiques ou congruents. En revanche, les faces adjacentes à une face donnée sont dans des plans perpendiculaires à celui de la face initiale..
Il peut également être envisagé orthoèdre comme un prisme orthogonal à base rectangulaire, dans lequel le angles dièdres formées par les plans de deux faces adjacentes à une arête commune, elles mesurent 90º. L'angle dièdre entre deux faces est mesuré à l'intersection des faces avec un plan perpendiculaire qui leur est commun.
De même, l'ortoèdre est un parallélépipède rectangle, puisque c'est ainsi que le parallélépipède est défini comme la figure volumétrique de six faces, parallèles deux à deux.
Dans tout parallélépipède, les faces sont des parallélogrammes, mais dans le parallélépipède rectangulaire les faces doivent être rectangulaires.
Index des articles
- 1 Parties de l'ortoèdre
- 2 formules d'orthoèdre
- 2.1 Zone
- 2.2 Volume
- 2.3 Diagonale interne
- 3 exemples
- 3.1 - Exemple 1
- 3.2 - Exercice 2
- 4 Références
Parties de l'ortoèdre
Les parties d'un polyèdre, comme l'orthoèdre, ils sont:
-Bords
-Sommets
-Visages
L'angle entre deux arêtes d'une face de l'orthoèdre coïncide avec l'angle dièdre formé par ses deux autres faces adjacentes à chacune des arêtes, formant un angle droit. L'image suivante clarifie chaque concept:
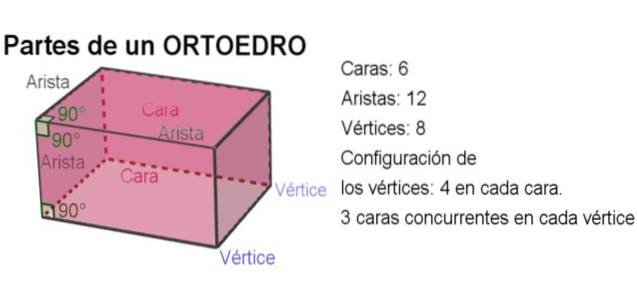
-Au total, un ortoèdre a 6 faces, 12 arêtes et 8 sommets..
-L'angle entre deux bords est un angle droit.
-L'angle dièdre entre deux faces est également correct.
-Dans chaque face, il y a quatre sommets et dans chaque sommet trois faces mutuellement orthogonales concourent.
Formules orthoèdres
Surface
La surface ou l'aire d'un orthoèdre est la somme des aires de leurs faces.
Si les trois arêtes qui se rencontrent à un sommet ont des mesures a, b et c, comme le montre la figure 3, alors la face avant a une aire c⋅b et la face inférieure a également une aire c⋅b.
Ensuite, les deux faces latérales ont une aire a⋅b chacune. Et enfin, les faces du sol et du plafond ont une surface avant JC chacune.
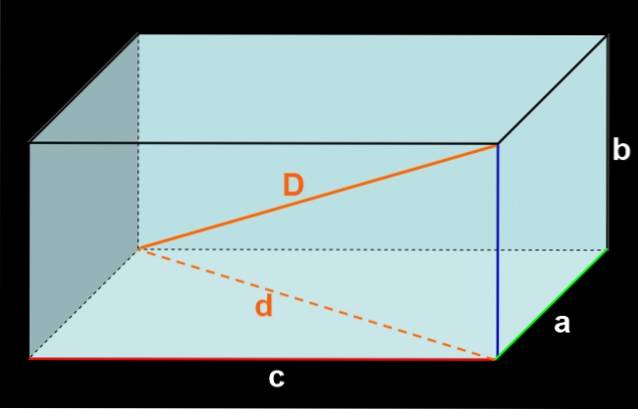
L'ajout de l'aire de toutes les faces donne:
A = 2⋅c⋅b + 2⋅a⋅b + 2⋅a⋅c
Prendre un facteur commun et ordonner les termes:
A = 2⋅ (a⋅b + b⋅c + c⋅a)
Le volume
Si l'orthoèdre est considéré comme un prisme, son volume est calculé comme suit:
Volume = Aire de la base du prisme x la hauteur du prisme
Dans ce cas, le plancher de dimensions est pris comme base rectangulaire c Oui à, alors la surface de la base est c⋅a.
La hauteur est donnée par la longueur b des arêtes orthogonales aux faces latérales à Oui c.
Multiplier la surface de la base (avant JC) par hauteur b tu as le volume V de l'ortoèdre:
V = a⋅b⋅c
Diagonale interne
Dans un orthoèdre, il existe deux types de diagonales: les diagonales externes et les diagonales internes.
Les diagonales externes sont sur les faces rectangulaires, tandis que les diagonales internes sont les segments qui joignent deux sommets opposés, étant compris par des sommets opposés ceux qui ne partagent aucune arête.
Dans un orthoèdre, il y a quatre diagonales internes, toutes de même mesure. La longueur des diagonales internes peut être obtenue en appliquant le théorème de Pythagore pour les triangles rectangles.
La longueur d de la diagonale externe de la face au sol de l'ortoèdre remplit la relation de Pythagore:
rédeux = adeux + cdeux
De même, la diagonale intérieure de la mesure D remplit la relation de Pythagore:
rédeux = ddeux + bdeux.
En combinant les deux expressions précédentes, nous avons:
rédeux = adeux + cdeux + bdeux.
Enfin, la longueur de l'une des diagonales internes de l'orthoèdre est donnée par la formule suivante:
D = √ (unedeux + bdeux + cdeux ).
Exemples
- Exemple 1
Un maçon construit une cuve en forme d'orthoèdre dont les dimensions internes sont: 6 mx 4 m de base et 2 m de hauteur. On demande:
a) Déterminez la surface intérieure du réservoir s'il est complètement ouvert en haut.
b) Calculer le volume de l'espace intérieur du réservoir.
c) Trouvez la longueur d'une diagonale intérieure.
d) Quelle est la capacité du réservoir en litres?
Solution pour
Nous prendrons les dimensions de la base rectangulaire a = 4 m et c = 6 m et la hauteur comme b = 2 m
L'aire d'un ortoèdre avec les dimensions données est donnée par la relation suivante:
A = 2⋅ (a⋅b + b⋅c + c⋅a) = 2⋅ (4 m⋅2 m + 2 m⋅6 m + 6 m⋅4 m)
C'est-à-dire:
A = 2⋅ (8 mdeux + 12 mdeux + 24 mdeux) = 2⋅ (44 mdeux) = 88 mdeux
Le résultat précédent est la surface de l'ortoèdre fermé aux dimensions données, mais puisqu'il s'agit d'un réservoir complètement découvert dans sa partie supérieure, pour obtenir la surface des parois intérieures du réservoir, la surface du couvercle manquant doit être soustrait, c'est-à-dire:
c⋅a = 6 m ⋅ 4 m = 24 mdeux.
Enfin, la surface intérieure du réservoir sera: S = 88 mdeux - 24 mdeux = 64 mdeux.
Solution b
Le volume intérieur du réservoir est donné par le volume d'un orthoèdre des dimensions intérieures du réservoir:
V = a⋅b⋅c = 4 m ⋅ 2 m ⋅ 6 m = 48 m3.
Solution c
La diagonale intérieure d'un octaèdre avec les dimensions de l'intérieur du réservoir a une longueur D donnée par:
√ (àdeux + bdeux + cdeux ) = √ ((4 m)deux + (2 m)deux + (6 m)deux )
Réaliser les opérations indiquées nous avons:
D = √ (16 mdeux + 4 mdeux + 36 mdeux ) = √ (56 mdeux) = 2√ (14) m = 7,48 m.
Solution d
Pour calculer la capacité du réservoir en litres, il faut savoir que le volume d'un décimètre cube est égal à la capacité d'un litre. Il était auparavant calculé en volume en mètres cubes, mais il faut le transformer en décimètres cubes puis en litres:
V = 48 m3 = 48 (10 dm)3 = 4 800 dm3 = 4 800 L
- Exercice 2
Un aquarium en verre a une forme cubique avec un côté de 25 cm. Déterminez la superficie en mdeux, le volume en litres et la longueur d'une diagonale intérieure en cm.
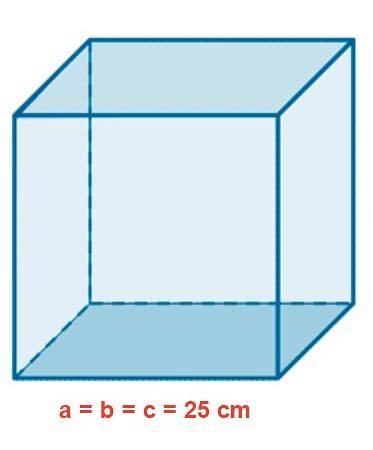
Solution
L'aire est calculée à l'aide de la même formule d'orthoèdre, mais en tenant compte du fait que toutes les dimensions sont identiques:
A = 2⋅ (3 a⋅a) = 6⋅ adeux = 6⋅ (25 cm)deux = 1 250 cmdeux
Le volume du cube est donné par:
V = a3 = (25 cm)3 = 15,625 cm3 = 15 625 (0,1 dm)3 = 15 625 dm3 = 15,625 L.
La longueur D de la diagonale intérieure est:
D = √ (3adeux) = 25√ (3) cm = 43,30 cm.
Les références
- Arias J. GeoGebra: Prisme. Récupéré de: youtube.com.
- Calculus.cc. Exercices et problèmes résolus de surfaces et de volumes. Récupéré de: calculo.cc.
- Salvador R. Pyramid + ortohedron avec GEOGEBRA (IHM). Récupéré de: youtube.com
- Weisstein, Eric. "Orthoèdre". MathWorld. Recherche Wolfram.
- Wikipédia. Orthoèdre Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.