UNE prisme trapézoïdal est un prisme tel que les polygones impliqués sont des trapèzes. La définition d'un prisme est un corps géométrique tel qu'il est formé de deux polygones égaux et parallèles et le reste de leurs faces sont des parallélogrammes.
Un prisme peut avoir différentes formes, qui dépendent non seulement du nombre de côtés du polygone, mais du polygone lui-même.
Si les polygones impliqués dans un prisme sont des carrés, alors ceci est différent d'un prisme impliquant des losanges par exemple, même si les deux polygones ont le même nombre de côtés. Par conséquent, cela dépend du quadrilatère impliqué..
Pour voir les caractéristiques d'un prisme trapézoïdal, il faut commencer par savoir comment il est dessiné, puis quelles propriétés remplit la base, quelle est sa surface et enfin comment son volume est calculé.
Pour le dessiner, il faut d'abord définir ce qu'est un trapèze.
Un trapèze est un polygone irrégulier à quatre côtés (quadrilatère), de sorte qu'il n'a que deux côtés parallèles appelés bases et la distance entre leurs bases est appelée hauteur..
Pour dessiner le prisme trapézoïdal droit, vous commencez par dessiner un trapèze. Ensuite, une ligne verticale de longueur "h" est projetée à partir de chaque sommet et enfin un autre trapèze est dessiné de telle sorte que ses sommets coïncident avec les extrémités des lignes précédemment dessinées..
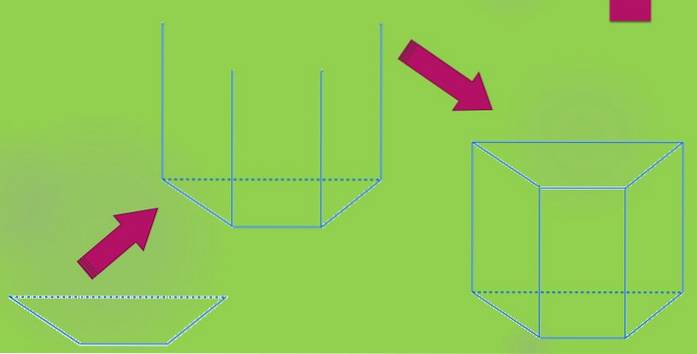
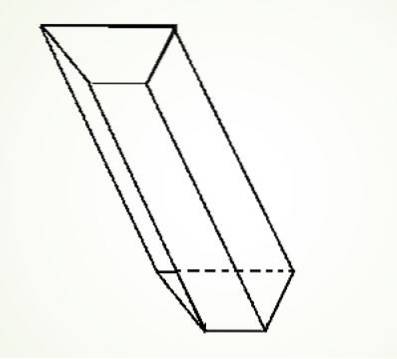
Vous pouvez également avoir un prisme trapézoïdal oblique, dont la construction est similaire au précédent, il vous suffit de tracer les quatre lignes parallèles les unes aux autres.
Comme indiqué précédemment, la forme du prisme dépend du polygone. Dans le cas particulier du trapèze, nous pouvons trouver trois types de bases différents:
-Trapèze rectangle: est-ce que ce trapèze est tel que l'un de ses côtés est perpendiculaire à ses côtés parallèles ou qu'il a simplement un angle droit.
-Trapèze isocèle: est un trapèze tel que ses côtés non parallèles ont la même longueur.
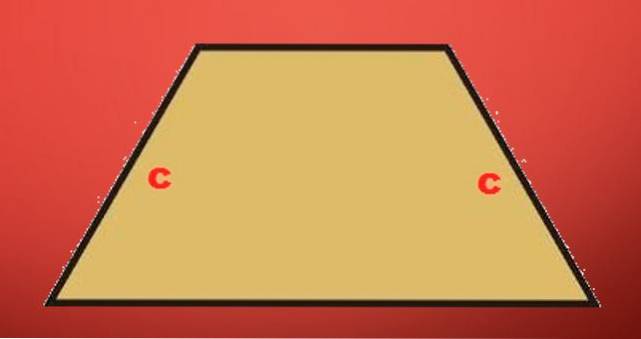
Trapèze scalène: c'est ce trapèze qui n'est pas isocèle ou un rectangle; ses quatre côtés ont des longueurs différentes.
Comme on peut le voir, selon le type de trapèze utilisé, un prisme différent sera obtenu.
Pour calculer la surface d'un prisme trapézoïdal, nous avons besoin de connaître l'aire du trapèze et l'aire de chaque parallélogramme impliqué..
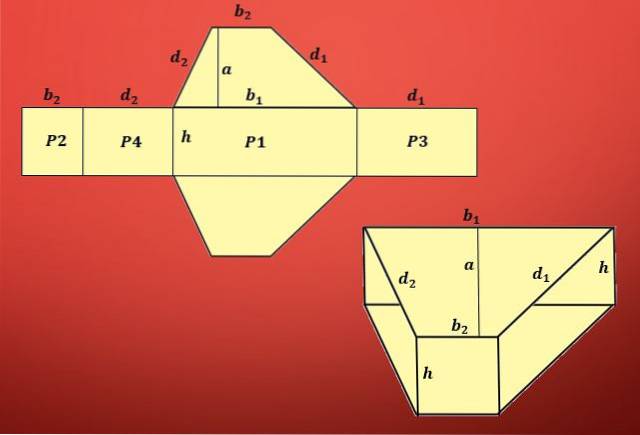
Comme on peut le voir sur l'image précédente, la zone comprend deux trapèzes et quatre parallélogrammes différents..
L'aire d'un trapèze est définie comme T = (b1 + b2) xa / 2 et les aires des parallélogrammes sont P1 = hxb1, P2 = hxb2, P3 = hxd1 et P4 = hxd2, où «b1» et «b2 »Sont les bases du trapèze,« d1 »et« d2 »les côtés non parallèles,« a »est la hauteur du trapèze et« h »la hauteur du prisme.
Par conséquent, la surface d'un prisme trapézoïdal est A = 2T + P1 + P2 + P3 + P4.
Puisque le volume d'un prisme est défini comme V = (aire du polygone) x (hauteur), on peut conclure que le volume d'un prisme trapézoïdal est V = Txh.
L'un des objets les plus courants qui ont la forme d'un prisme trapézoïdal est un lingot d'or ou les rampes utilisées dans les courses de motos..
Personne n'a encore commenté ce post.