En un processus isobare, la pression P d'un système reste constant. Le préfixe "iso" vient du grec et est utilisé pour indiquer que quelque chose reste constant, tandis que "baros", également du grec, signifie poids.
Les processus isobares sont très typiques à la fois dans des conteneurs fermés et dans des espaces ouverts, étant faciles à localiser dans la nature. Nous entendons par là qu'il existe des changements physiques et chimiques possibles à la surface de la terre ou des réactions chimiques dans des conteneurs ouverts à l'atmosphère..
Quelques exemples sont obtenus en chauffant un ballon rempli d'air au soleil, en cuisinant, en faisant bouillir ou en congelant de l'eau, de la vapeur générée dans des chaudières, ou en élevant une montgolfière. Plus tard, nous donnerons une explication de ces cas.
Index des articles
Dérivons une équation pour le processus isobare en supposant que le système étudié est un gaz parfait, un modèle tout à fait approprié pour presque tous les gaz à moins de 3 atmosphères de pression. Les particules de gaz parfait se déplacent au hasard, occupant tout le volume de l'espace qui les contient sans interagir les unes avec les autres..
Si le gaz idéal enfermé dans un cylindre équipé d'un piston mobile est autorisé à se dilater lentement, on peut supposer que ses particules sont en équilibre à tout moment. Puis le gaz s'exerce sur le piston de zone À une force F de grandeur:
F = p.A
Où p est la pression du gaz. Cette force exerce un travail produisant un déplacement infinitésimal dx sur le piston donné par:
dW = Fdx = pA.dx
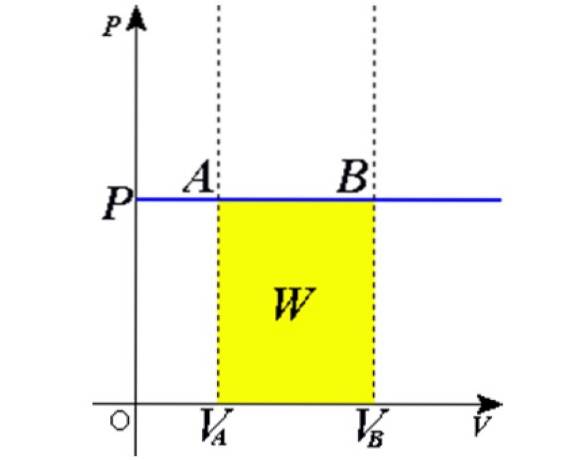
En tant que produit Adx est un différentiel de volume dV, ensuite dW = pdV. Il reste à intégrer les deux faces du volume initial VÀ jusqu'au volume final VB pour obtenir le travail total effectué par le gaz:
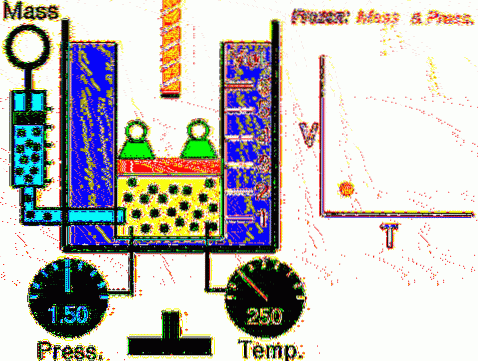
La situation décrite est vérifiée expérimentalement en confinant un gaz à l'intérieur d'un cylindre muni d'un piston mobile, comme le montrent les figures 2 et 3. Un poids de masse M est placé sur le piston, dont le poids est dirigé vers le bas, tandis que le gaz exerce une force ascendante grâce à la pression P produite sur le piston.
Le piston pouvant se déplacer librement, le volume qu'occupe le gaz peut changer sans problème, mais la pression reste constante. Ajout de la pression atmosphérique Pau m, qui exerce également une force descendante, nous avons:
Mg - P.A + Pau m . A = constante
Par conséquent: P = (Mg / A) + Pau m il ne varie pas, sauf si M et donc le poids sont modifiés. En ajoutant de la chaleur au cylindre, le gaz se dilatera en augmentant son volume ou il se contractera lors de l'extraction de la chaleur..
L'équation d'état des gaz parfaits relie les variables d'importance: pression P, volume V et température T:
P.V = n .R.T
Ici n représente le nombre de moles et R est la constante de gaz idéale (valable pour tous les gaz), qui est calculée en multipliant la constante de Boltzmann par le nombre d'Avogadro, ce qui donne:
R = 8,31 J / mol K
Lorsque la pression est constante, l'équation d'état peut s'écrire:
V / T = nR / P
Mais nR / P est constant, puisque n, R et P le sont. Ainsi, lorsque le système passe de l'état 1 à l'état 2, la proportion suivante apparaît, également connue sous le nom de loi de Charles:
V1/ T1 = Vdeux/ Tdeux
Substituer dans W = PΔV, le travail effectué pour passer de l'état 1 à l'état 2 est obtenu, en termes de constantes et de variation de température, facile à mesurer avec un thermomètre:
W1 → 2 = nR (Tdeux - T1) = nR.ΔT
D'autre part, la première loi de la thermodynamique stipule que:
∆U = Q - W
Cela signifie que l'ajout d'une certaine quantité de chaleur Q au gaz augmente l'énergie interne ∆U et augmente les vibrations de ses molécules. De cette façon, le gaz se dilate et fonctionne en déplaçant le piston, comme nous l'avons déjà dit..
Dans un gaz parfait monoatomique et la variation de l'énergie interne ∆U, qui comprend à la fois l'énergie cinétique et l'énergie potentielle de ses molécules, est:
∆U = (3/2)nR ΔT
Enfin, nous combinons les expressions que nous avons obtenues en une seule:
Q = ∆U + W = (3/2)nR ΔT + nR∆T = (5/2) nR ΔT
Alternativement, Q peut être réécrit en termes de masse m, de différence de température et d'une nouvelle constante appelée chaleur spécifique du gaz à pression constante, abrégé cp, dont les unités sont J / mol K:
Q = m cp ∆T
Tous les processus isobares ne sont pas effectués dans des conteneurs fermés. En fait, d'innombrables processus thermodynamiques de toutes sortes se produisent à la pression atmosphérique, de sorte que les processus isobares sont très fréquents dans la nature. Cela comprend les changements physiques et chimiques à la surface de la terre, les réactions chimiques dans les vaisseaux ouverts à l'atmosphère, et bien plus encore..
Pour que les processus isobares se produisent dans des systèmes fermés, leurs limites doivent être suffisamment flexibles pour permettre des changements de volume sans faire varier la pression.
C'est ce qui s'est passé dans l'expérience du piston qui se déplaçait facilement lorsque le gaz se dilatait. La même chose se produit en enfermant un gaz dans un ballon de fête ou une montgolfière.
Nous avons ici plusieurs exemples de processus isobares:
L'eau bouillante pour le thé ou la cuisson des sauces dans des récipients ouverts sont de bons exemples de processus isobares, puisqu'ils ont tous lieu à la pression atmosphérique..
Au fur et à mesure que l'eau est chauffée, la température et le volume augmentent et si de la chaleur continue à être ajoutée, le point d'ébullition est finalement atteint, dans lequel le changement de phase de l'eau de liquide à vapeur d'eau se produit. Pendant ce temps, la température reste également constante à 100 ° C..
D'autre part, la congélation de l'eau est également un processus isobare, qu'elle se déroule dans un lac en hiver ou dans le réfrigérateur domestique..
Un autre exemple de processus isobare est la variation du volume d'un ballon gonflé à l'air lorsqu'il est laissé exposé au soleil. Première chose le matin, quand il ne fait pas encore très chaud, le ballon a un certain volume..
Au fur et à mesure que le temps passe et que la température augmente, le ballon chauffe également, augmentant son volume et tout cela se produit à pression constante. Le matériau du ballon est un bon exemple de bordure suffisamment flexible pour que l'air à l'intérieur, lorsqu'il est chauffé, se dilate sans modifier la pression.
L'expérience peut également être réalisée en ajustant le ballon non gonflé dans le bec d'une bouteille en verre remplie d'un tiers d'eau, qui est chauffée au bain-marie. Dès que l'eau est chauffée, le ballon se gonfle immédiatement, mais il faut faire attention à ne pas trop chauffer pour qu'il n'explose pas..
C'est un navire flottant sans propulsion, qui utilise les courants d'air pour transporter des personnes et des objets. Le ballon est généralement rempli d'air chaud, qui, étant plus froid que l'air environnant, monte et se dilate, provoquant la montée du ballon..
Bien que les courants d'air dirigent le ballon, il a des brûleurs qui sont activés pour chauffer le gaz lorsque l'on souhaite monter ou maintenir l'altitude, et se désactivent lors de la descente ou de l'atterrissage. Tout cela se passe à la pression atmosphérique, supposée constante à une certaine hauteur non loin de la surface..
La vapeur est générée dans les chaudières en chauffant l'eau et en maintenant la pression constante. Ensuite, cette vapeur effectue un travail utilisable, par exemple la production d'électricité dans des centrales thermoélectriques ou l'activation d'autres mécanismes tels que des locomotives et des pompes à eau..
Il y a 40 litres de gaz à une température de 27 ºC. Trouvez l'augmentation de volume lorsque la chaleur est ajoutée de manière isobare jusqu'à atteindre 100 ºC.
La loi de Charles est utilisée pour déterminer le volume final, mais attention: les températures doivent être exprimées en kelvin, en ajoutant simplement 273 K à chacune:
27 ºC = 27 + 273 K = 300 K
100 ºC = 100 + 273 K = 373 K
A partir de:
V1/ T1 = Vdeux/ Tdeux ⇒ Vdeux = Tdeux(V1/ T1) = 373 ºC (40 L / 300 K) = 49,7 L
Enfin l'augmentation de volume est Vdeux - V1 = 49,7 L - 40 L = 9,7 L.
Livré 5,00 x 103 J d'énergie à un gaz idéal pour effectuer 2,00 x 103 J travaillant sur son environnement dans un processus isobare. Il est demandé de trouver:
a) Le changement de l'énergie interne du gaz.
b) Le changement de volume, si maintenant l'énergie interne diminue de 4,50 x 103 J et 7,50 x 10 sont éjectés3 J du système, en considérant une pression constante de 1,01 x 105 Pennsylvanie.
On utilise ∆U = Q - W et les valeurs données dans la déclaration sont remplacées: Q = 5,00 x 103 J et W = 2,00 x 103 J:
=5,00 x 103 J - 2,00 x 103 J = 3,00 x 103 J
Par conséquent, l'énergie interne du gaz augmente de 3,00 x 103 J.
Le changement de volume se retrouve dans le travail effectué: W = P∆V:
∆U = Q - W = Q - P∆V
La déclaration indique que l'énergie interne diminue, donc: ∆U= -4,50 x 103 J. Cela nous dit également qu'une certaine quantité de chaleur est expulsée: Q = -7,50 x 103 Dans les deux cas, le signe négatif représente la diminution et la perte, donc:
-4,50 x 103 J = -7,50 x 103 J - P∆V
Où P = 1,01 x 105 Pa. Comme toutes les unités sont dans le système international, nous procédons à la résolution du changement de volume:
∆V = (-4,50 x 103 J + 7,50 x 103 J) / (- 1,01 x 105 Pennsylvanie) = -2,97 x 10-deux m3
Puisque le changement de volume est négatif, cela signifie que le volume a diminué, c'est-à-dire que le système s'est contracté.
Personne n'a encore commenté ce post.