
Test U de Mann - Whitney ce que c'est et quand il est appliqué, exécution, exemple
La Test U de Mann-Whitney Il est appliqué pour la comparaison de deux échantillons indépendants lorsqu'ils ont peu de données ou ne suivent pas une distribution normale. De cette manière, il est considéré comme un test non paramétrique, Contrairement à son homologue le Test t de l'étudiant, qui est utilisé lorsque l'échantillon est suffisamment grand et suit la distribution normale.
Frank Wilcoxon l'a proposé pour la première fois en 1945, pour des échantillons de tailles identiques, mais deux ans plus tard, il a été prolongé pour le cas d'échantillons de tailles différentes par Henry Mann et D. R. Whitney.
Le test est souvent appliqué pour vérifier s'il existe une relation entre une variable qualitative et une variable quantitative.
Un exemple illustratif consiste à prendre un ensemble de personnes hypertendues et à extraire deux groupes, à partir desquels les données quotidiennes de pression artérielle sont enregistrées pendant un mois..
Le traitement A est appliqué à un groupe et le traitement B. est appliqué à un autre. Ici, la tension artérielle est la variable quantitative et le type de traitement est la variable qualitative..
Nous voulons savoir si la médiane, et non la moyenne, des valeurs mesurées est statistiquement identique ou différente, pour établir s'il y a une différence entre les deux traitements. Pour obtenir la réponse, la statistique de Wilcoxon ou le test U de Mann-Whitney est appliqué..
Index des articles
- 1 Énoncé du problème dans le test U de Mann-Whitney
- 1.1 Variables qualitatives versus variables quantitatives
- 2 Caractéristiques du test Mann Whitney U
- 2.1 Formule de Mann - Whitney
- 2.2 Étapes pour appliquer le test
- 3 Exemple d'application pratique
- 3.1 - Étape 1
- 3.2 - Étape 2
- 3.3 Étape 3
- 3.4 Étape 4
- 4 calculatrices en ligne pour le test U de Mann - Whitney
- 5 Références
Énoncé du problème dans le test U de Mann-Whitney
Un autre exemple dans lequel le test peut être appliqué est le suivant:
Supposons que vous souhaitiez savoir si la consommation de boissons gazeuses diffère significativement dans deux régions du pays.
L'une d'elles s'appelle la région A et l'autre la région B.Un registre est tenu des litres consommés chaque semaine dans deux échantillons: l'un de 10 personnes pour la région A et un autre de 5 personnes pour la région B.
Les données sont les suivantes:
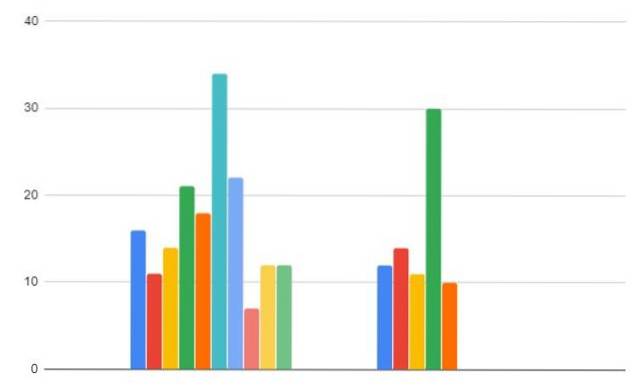
-Région A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
-Région B: 12,14, 11, 30, 10
La question suivante se pose:
La consommation de boissons non alcoolisées (Y) dépend-elle de la région (X)?
Variables qualitatives versus variables quantitatives
-Variable qualitative X: Région
-Variable quantitative Y: Consommation de soude
Si la quantité de litres consommés est la même dans les deux régions, la conclusion sera qu'il n'y a pas de dépendance entre les deux variables. Le moyen de le savoir est de comparer la tendance moyenne ou médiane des deux régions.
Cas normal
Si les données suivent une distribution normale, deux hypothèses sont soulevées: le nul H0 et l'alternative H1 par la comparaison entre les moyennes:
-H0: il n'y a pas de différence entre la moyenne des deux régions.
-H1: les moyennes des deux régions sont différentes.
Cas avec tendance anormale
Au contraire, si les données ne suivent pas une distribution normale ou si l'échantillon est tout simplement trop petit pour le savoir, au lieu de comparer la moyenne, il serait comparé la médiane des deux régions.
-H0: il n'y a pas de différence entre la médiane des deux régions.
-H1: les médianes des deux régions sont différentes.
Si les médianes coïncident, alors l'hypothèse nulle est remplie: il n'y a pas de relation entre la consommation de boissons gazeuses et la région.
Et si le contraire se produit, l'hypothèse alternative est vraie: il y a une relation entre consommation et région.
C'est pour ces cas où le test U de Mann-Whitney est indiqué..
Échantillons appariés ou non appariés
La prochaine question importante pour décider d'appliquer ou non le test Mann Whitney U est de savoir si le nombre de données dans les deux échantillons est identique, c'est-à-dire qu'elles sont égales..
Si les deux échantillons sont appariés, la version originale de Wilcoxon s'appliquerait. Mais sinon, comme c'est le cas dans l'exemple, alors le test de Wilcoxon modifié est appliqué, qui est précisément le test U de Mann Whitney..
Caractéristiques du test Mann Whitney U
Le test Mann-Whitney U est un test non paramétrique, applicable aux échantillons qui ne suivent pas la distribution normale ou avec peu de données. Il présente les caractéristiques suivantes:
1.- Comparez les médianes
2.- Il fonctionne sur des gammes ordonnées
3.- Il est moins puissant, étant entendu par la puissance la probabilité de rejeter l'hypothèse nulle alors qu'elle est effectivement fausse.
Compte tenu de ces caractéristiques, le test Mann-Whitney U est appliqué lorsque:
-Les données sont indépendantes
-Ils ne suivent pas la distribution normale
-L'hypothèse nulle H0 est acceptée si les médianes des deux échantillons coïncident: Ma = Mb
-L'hypothèse alternative H1 est acceptée si les médianes des deux échantillons diffèrent: Ma ≠ Mb
Mann - formule Whitney
La variable U est la statistique de contraste utilisée dans le test de Mann-Whitney et est définie comme suit:
U = min (Ua, Ub)
Cela signifie que U est la plus petite des valeurs entre Ua et Ub, appliquée à chaque groupe. Dans notre exemple, ce serait pour chaque région: A ou B.
Les variables Ua et Ub sont définies et calculées selon la formule suivante:
Ua = Na Nb + Na (Na +1) / 2 - Ra
Ub = Na Nb + Nb (Nb +1) / 2 - Rb
Ici les valeurs Na et Nb sont les tailles des échantillons correspondant respectivement aux régions A et B et pour leur part, Ra et Rb sont les sommes de rang que nous définirons ci-dessous.
Étapes pour appliquer le test
1.- Commandez les valeurs des deux échantillons.
2.- Attribuez un rang d'ordre à chaque valeur.
3.- Corriger les ligatures existantes dans les données (valeurs répétées).
4.- Calculer Ra = Somme des plages de l'échantillon A.
5.- Trouver Rb = Somme des rangs de l'échantillon B.
6.- Déterminer la valeur Ua et Ub, selon les formules données dans la section précédente.
7.- Comparez Ua et Ub, et la plus petite des deux est affectée à la statistique U expérimentale (c'est-à-dire des données) qui est comparée à la statistique U théorique ou normale.
Exemple d'application pratique
Maintenant, nous appliquons ce qui précède au problème des boissons gazeuses soulevé précédemment:
Région A: 16, 11, 14, 21, 18, 34, 22, 7, 12, 12
Région B: 12,14, 11, 30, 10
Selon que les moyennes des deux échantillons sont statistiquement identiques ou différentes, l'hypothèse nulle est acceptée ou rejetée: il n'y a pas de relation entre les variables Y et X, c'est-à-dire que la consommation de boissons gazeuses ne dépend pas de la région:
H0: Ma = Mb
H1: Ma ≠ Mb
- Étape 1
Nous procédons à l'ordre des données conjointement pour les deux échantillons, en ordonnant les valeurs de la plus basse à la plus élevée:

Notez que la valeur 11 apparaît 2 fois (une fois dans chaque échantillon). À l'origine, il a des positions ou des plages 3 et 4, mais afin de ne pas surestimer ou sous-estimer l'une ou l'autre, la valeur moyenne est choisie comme plage, soit 3,5.
De même, on procède avec la valeur 12, qui est répétée trois fois avec les plages 5, 6 et 7.
Eh bien, la valeur 12 se voit attribuer la plage moyenne de 6 = (5 + 6 + 7) / 3. Et de même pour la valeur 14, qui a une ligature (apparaît dans les deux échantillons) aux positions 8 et 9, on lui attribue la plage moyenne 8,5 = (8 + 9) / 2.
- Étape 2
Ensuite, les données des régions A et B sont à nouveau séparées, mais maintenant leurs plages correspondantes leur sont affectées dans une autre ligne:
Région A

Région B

Les plages Ra et Rb sont obtenues à partir des sommes des éléments de la deuxième ligne pour chaque cas ou région.
Étape 3
Les valeurs respectives Ua et Ub sont calculées:
Ua = 10 × 5 + 10 (10 + 1) / 2 - 86 = 19
Ub = 10 × 5 + 5 (5 + 1) / 2-34 = 31
Valeur expérimentale U = min (19, 31) = 19
Étape 4
On suppose que le U théorique suit une distribution normale N avec des paramètres donnés exclusivement par la taille des échantillons:
N ((na⋅nb) / 2, √ [na nb (na + nb +1) / 12])
Afin de comparer la variable U obtenue expérimentalement, avec le U théorique, il est nécessaire de changer la variable. On passe de la variable expérimentale U à sa valeur typifié, qui sera appelé Z, afin de pouvoir faire la comparaison avec celle d'une distribution normale normalisée.
Le changement de variable est le suivant:
Z = (U - na.nb / 2) / √ [nd. nb (nd + nb + 1) / 12]
Il est à noter que pour le changement de variable on a utilisé les paramètres de la distribution théorique pour U. Ensuite, la nouvelle variable Z, qui est un hybride entre le U théorique et le U expérimental, est comparée à une distribution normale normalisée N (0 , 1).
Critères de comparaison
Si Z ≤ Zα ⇒ l'hypothèse nulle H0 est acceptée
Si Z> Zα ⇒ l'hypothèse nulle H0 est rejetée
Les valeurs critiques standardisées Zα dépendent du niveau de confiance requis, par exemple pour un niveau de confiance α = 0,95 = 95%, qui est le plus courant, la valeur critique Zα = 1,96.
Pour les données présentées ici:
Z = (U - na nb / 2) / √ [na nb (na + nb + 1) / 12] = -0,73
Qui est en dessous de la valeur critique 1,96.
La conclusion finale est donc que l'hypothèse nulle H0 est acceptée:
Il n'y a pas de différence de consommation de boissons gazeuses entre les régions A et B.
Calculateurs en ligne pour le test Mann - Whitney U
Il existe des programmes spécifiques pour les calculs statistiques, notamment SPSS et MINITAB, mais ces programmes sont payants et leur utilisation n'est pas toujours aisée. Cela est dû au fait qu'ils offrent tellement d'options, que pratiquement leur utilisation est réservée aux experts en statistiques..
Heureusement, il existe plusieurs programmes en ligne très précis, gratuits et faciles à utiliser qui vous permettent d'exécuter le test Mann-Whitney U, entre autres..
Ces programmes sont:
-Social Science Statistics (socscistatistics.com), qui a à la fois le test U de Mann-Whitney et le test de Wilcoxon pour le cas d'échantillons équilibrés ou appariés.
-AI Therapy Statistics (ai-therapy.com), qui possède plusieurs des tests habituels de statistiques descriptives.
-Statistique à utiliser (physics.csbsju.edu/stats), l'une des plus anciennes, donc son interface peut paraître datée, bien qu'il s'agisse néanmoins d'un programme gratuit très efficace.
Les références
- Dietrichson. Méthodes quantitatives: test de classement. Récupéré de: bookdown.org
- Guide Marín J P. SPSS: Analyse et procédures dans les tests non paramétriques. Récupéré de: halweb.uc3m.es
- MOOC USAL. Tests non paramétriques: Mann - Whitney U. Récupéré de: youtube.com
- Wikipédia. Test U de Mann-Whitney. Récupéré de: es.wikipedia.com
- XLSTAT. Centre d'aide. Mann - Tutoriel de test Whitney dans Excel. Récupéré de: help.xlsat.com



Personne n'a encore commenté ce post.