La optique géométrique est la branche de la physique qui se concentre sur l'étude de la manière dont la lumière se diffuse et se réfléchit lorsqu'elle passe d'un milieu à un autre, sans tenir compte des effets de diffraction.
De cette manière, la lumière est représentée géométriquement par des rayons, des lignes imaginaires perpendiculaires aux fronts d'ondes lumineuses..
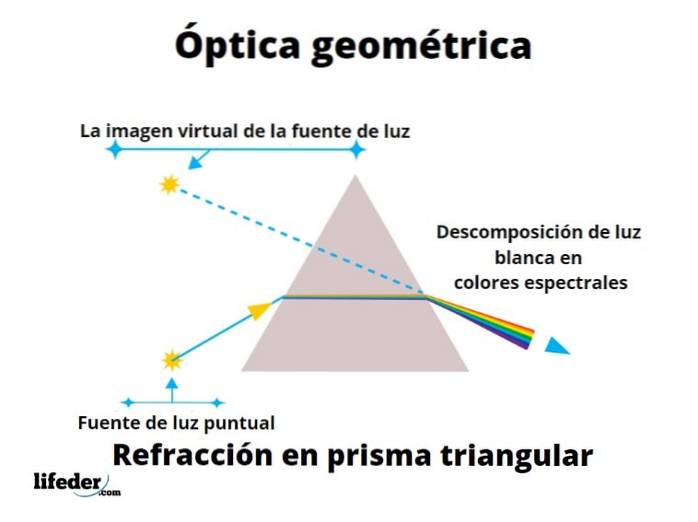
Des rayons de lumière émergent de sources lumineuses telles que le soleil, une flamme ou une ampoule, se propageant dans toutes les directions. Les surfaces reflètent en partie ces rayons de lumière et c'est pourquoi nous pouvons les voir, grâce au fait que les yeux contiennent des éléments sensibles à la lumière.
Grâce au traitement par rayons, l'optique géométrique ne prend pas tellement en compte les aspects ondulatoires de la lumière, mais explique plutôt comment les images se forment dans l'œil, les miroirs et les projecteurs, où elles le font et comment elles apparaissent.
Les principes fondamentaux de l'optique géométrique sont la réflexion et la réfraction de la lumière. Les rayons lumineux frappent à certains angles sur les surfaces qu'ils rencontrent, et grâce à cela une géométrie simple aide à garder une trace de leur trajectoire dans chaque milieu.
Cela explique des choses de tous les jours comme regarder notre image dans le miroir de la salle de bain, voir une cuillère à café qui semble se plier dans un verre rempli d'eau ou améliorer la vision avec des lunettes appropriées..
Nous avons besoin de lumière pour nous rapporter à l'environnement, c'est pourquoi son comportement a toujours étonné les observateurs, qui se sont interrogés sur sa nature..
Index des articles
L'optique géométrique étudie la propagation de la lumière dans le vide et dans divers milieux, sans expliquer en quoi consiste sa vraie nature. Pour cela, il utilise le modèle de rayon et la géométrie simple.
Un rayon est le chemin que la lumière suit dans un certain milieu transparent, ce qui est une excellente approximation tant que la longueur d'onde est petite par rapport à la taille des objets..
Cela est vrai dans de nombreux cas quotidiens, tels que ceux mentionnés au début..
Il y a deux prémisses fondamentales de l'optique géométrique:
-La lumière se propage de manière rectiligne.
-En se propageant à travers divers milieux, la lumière le fait selon des lois empiriques, c'est-à-dire obtenues par expérimentation.
La vitesse de la lumière dans un milieu matériel est différente de celle d'un vide. Là on sait qu'il est de 300 000 km / s, mais dans les airs c'est juste un peu plus bas, et encore plus dans l'eau ou le verre..
L'indice de réfraction est une grandeur sans dimension, qui est définie comme le quotient entre la vitesse à laquelle la lumière se déplace dans le vide cou alors et vitesse c dans ledit support:
n = cou alors / c
C'est le produit entre la distance parcourue par la lumière pour passer d'un point à un autre, et l'indice de réfraction du milieu:
L = s. n
Où L est le chemin optique, s est la distance entre les deux points et n représente l'indice de réfraction, en supposant constant.
Au moyen du chemin optique, les rayons lumineux se déplaçant dans différents supports sont comparés.
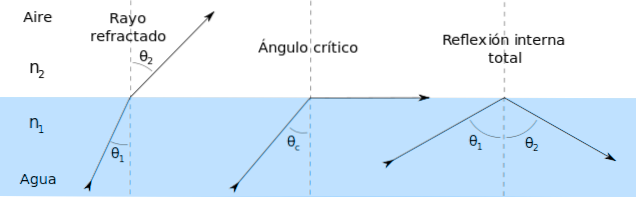
C'est l'angle que forme le rayon lumineux avec la ligne normale à une surface qui sépare deux médias.
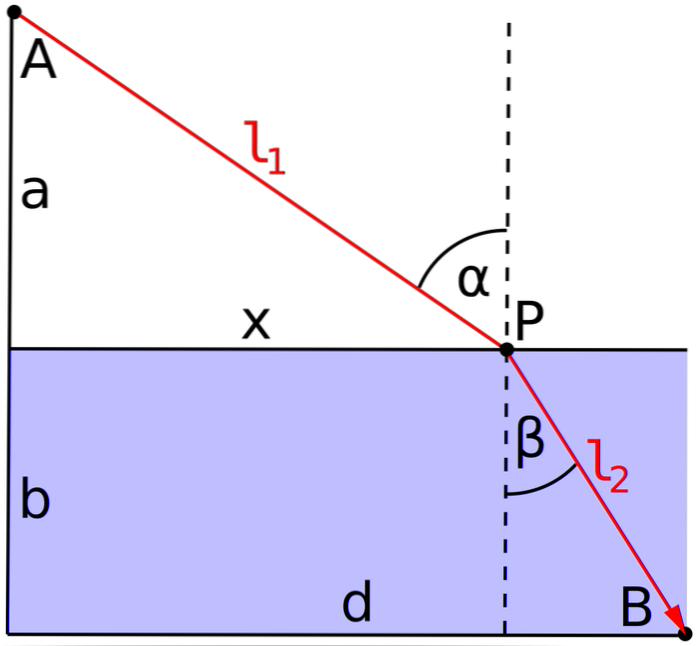
Le mathématicien français Pierre de Fermat (1601-1665) a noté que:
Lorsqu'un rayon de lumière se déplace entre deux points, il suit le chemin dans lequel il prend le minimum de temps.
Et comme la lumière se déplace à vitesse constante, son chemin doit être rectiligne.
En d'autres termes, le principe de Fermat stipule que le trajet du rayon lumineux est tel que le trajet optique entre deux points est minimal..
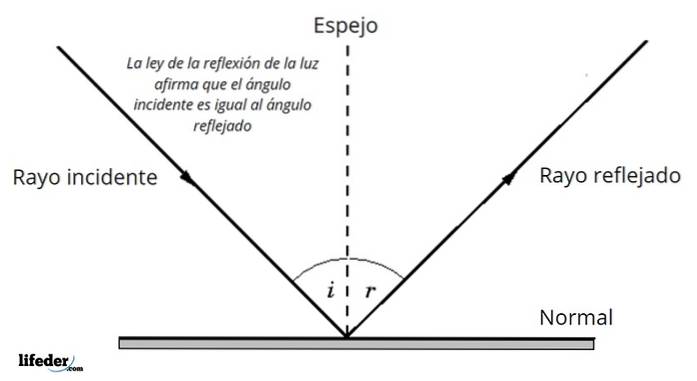
Lorsqu'on frappe la surface qui sépare deux milieux différents, une partie du rayon incident - ou la totalité de celui-ci - est réfléchie et le fait avec le même angle mesuré par rapport à la normale à la surface avec laquelle il a frappé..
En d'autres termes, l'angle d'incidence est égal à l'angle de réflexion:
θje = θje '
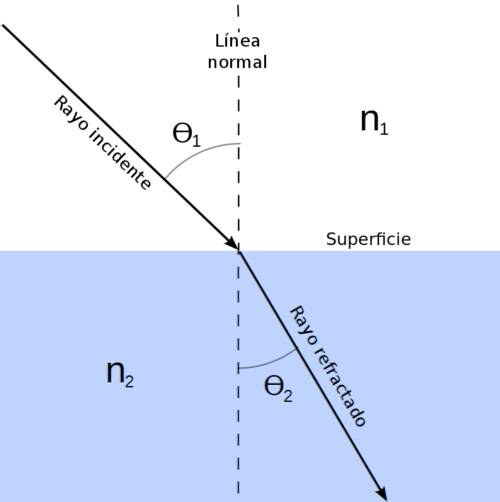
Le mathématicien néerlandais Willebrord Snell (1580-1626) a soigneusement observé le comportement de la lumière lorsqu'elle passe de l'air à l'eau et au verre.
Il a vu que lorsqu'un rayon de lumière tombe sur la surface qui sépare deux médias, formant un certain angle avec lui, une partie du rayon est réfléchie vers le premier milieu et l'autre continue son chemin à travers le second..
Il en déduit ainsi la relation suivante entre les deux médias:
n1 ⋅ sen θ1 = n2 ⋅ sen θdeux
Où1 et ndeux sont les respectifs indices de réfraction, tandis que θ1 Oui θdeux sont les angles d'incidence et de réfraction, mesurés par rapport à la normale à la surface, selon la figure ci-dessus.
Les miroirs sont des surfaces hautement polies qui réfléchissent la lumière des objets, permettant la formation d'images. Les miroirs plats, comme ceux de la salle de bain ou ceux portés dans un sac à main, sont courants.
Une lentille consiste en un dispositif optique avec deux surfaces réfractives très proches. Lorsqu'un faisceau de rayons parallèles traverse une lentille convergente, ils convergent en un point, formant une image. Lorsqu'il s'agit d'une lentille divergente, le contraire se produit: les rayons du faisceau divergent en un point.
Les lentilles sont fréquemment utilisées pour corriger les erreurs de réfraction dans l'œil, ainsi que dans divers instruments de grossissement optique..
Il existe des instruments optiques qui permettent d'agrandir les images, par exemple des microscopes, des loupes et des télescopes. Il y a aussi ceux pour regarder au-dessus du niveau des yeux, comme les périscopes.
Les caméras photographiques sont utilisées pour capturer et conserver les images, qui contiennent un système d'objectif et un élément d'enregistrement pour enregistrer l'image formée..
C'est un matériau long, fin et transparent à base de silice ou de plastique, utilisé pour la transmission de données. Il profite de la propriété de réflexion totale: lorsque la lumière atteint le milieu sous un certain angle, aucune réfraction ne se produit, donc le rayon peut parcourir de longues distances, rebondissant à l'intérieur du filament.
Les objets au fond d'une piscine ou d'un étang semblent être plus proches qu'ils ne le sont réellement, ce qui est dû à la réfraction. À quelle profondeur apparente un observateur voit-il une pièce qui se trouve au fond d'une piscine de 4 m de profondeur??
Supposons que le rayon sortant de la pièce atteigne l'œil de l'observateur à un angle de 40 ° par rapport à la normale..
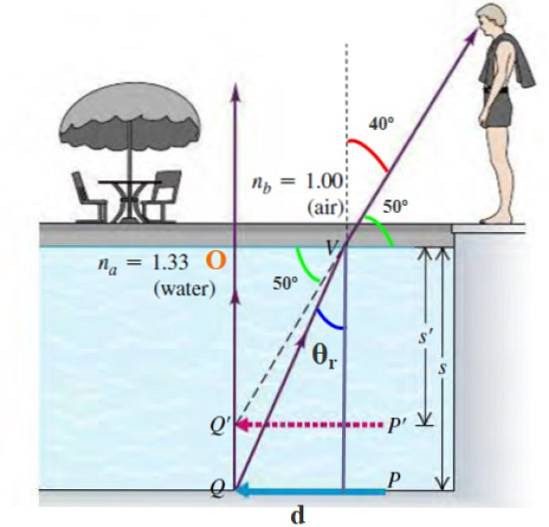
Fait: l'indice de réfraction de l'eau est de 1,33, celui de l'air est de 1.
La profondeur apparente de la pièce est de s 'et la profondeur de la piscine est de s = 4 m. La pièce est au point Q et l'observateur la voit au point Q '. La profondeur de ce point est:
s '= s - Q'Q
De la loi de Snell:
nb ⋅ sin 40º = nà ⋅ sen θr
sen θr = (nb ⋅ sin 40º) ÷ nà = sin 40º / 1,33 = 0,4833
θr = arcsen (0.4833) = 28.9º
Connaissant cet angle, nous calculons la distance d = OV du triangle rectangle, dont l'angle aigu est θr:
tan 28,9 ° = OV / 4 m
VO = 4m × bronzage 28,9º = 2,154 m
D'autre part:
tan 50º = OQ '/ OV
Donc:
OQ '= OV × tan 50º = 2,154 m × tan 50º = 2,57 m.
Personne n'a encore commenté ce post.