
Qu'est-ce qu'un angle périgonal? 5 exemples à comprendre
Les angles périgonaux, également appelés complets et entiers, sont ceux dans lesquels les côtés de leur angle coïncident, ce qui équivaut à quatre angles droits mesurant 360º.
En géométrie plane, un angle est une figure composée de deux segments de ligne, appelés rayons, qui se rencontrent à une extrémité: le sommet.
Pour distinguer ces lignes, elles sont marquées des lettres A et B, A étant le point d'origine (le rayon qui reste fixe) et B le point extrême (le rayon qui se déplace pour former l'ouverture).
L'écart entre les segments de ligne faisant partie d'un angle est mesuré en degrés (°) et est appelé amplitude; Cette mesure permet de classer les angles en quatre types:
1 - Angles aigus: ils ont une amplitude inférieure à 90 °.
2 - Angles droits: ils ont une amplitude d'exactement 90 °.
3 - angles obtus: ont une amplitude supérieure à 90 ° et inférieure à 180 °.
4 - Angles concaves:
-Angles plats: ont une largeur de 180 °.
-Angles réflexes: ont une amplitude supérieure à 180 ° mais inférieure à 360 °.
-Angles périgonaux: ils ont une amplitude de 360 °. Ils sont également appelés angles complets et angles entiers..
En ce sens, on observe que l'angle périgonal, lorsqu'il mesure 360 °, forme une circonférence. De même, les angles périgonaux peuvent résulter de la somme d'autres angles de plus petite amplitude, par exemple, quatre angles droits forment un périgonal.
L'angle périgonal est un angle concave
Les angles concaves sont ceux qui ont une amplitude comprise entre 180 ° et 360 °.
En ce sens, il existe trois types d'angles concaves: plats (180 °), réflexions (supérieures à 180 ° mais inférieures à 360 °) et périgonales (360 °).
L'angle périgonal et les circonférences
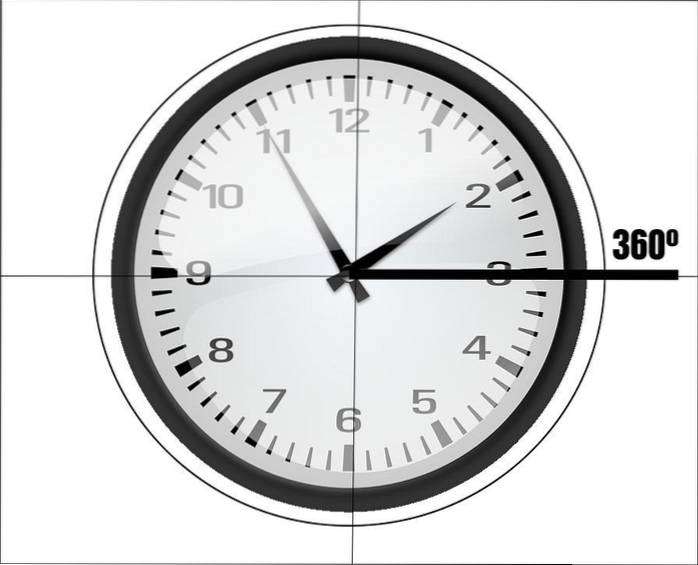
L'angle périgonal est égal à la largeur d'un cercle, soit 2 radians (360 °). Cela signifie que les angles périgonaux se forment lorsque l'un des rayons effectue un tour complet par rapport à l'autre rayon en se positionnant sur celui-ci. Par exemple, les aiguilles d'horloge forment des angles périgonaux.
En ce sens, comme les circonférences, les angles périgonaux peuvent être subdivisés en quadrants (1/4 de la circonférence), radians (1/2 de la circonférence), entre autres divisions.
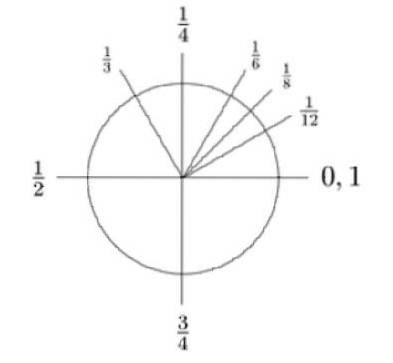
L'angle périgonal: fin et origine
Comme expliqué ci-dessus, à chaque angle, il y a un rayon qui s'appelle l'extrême et un autre qui s'appelle l'origine. ET
n les angles périgonaux, l'extrémité et l'origine sont dans la même position, puisque l'extrémité a fait un tour complet par rapport à l'origine.
L'angle périgonal et les angles consécutifs
Les angles consécutifs sont ceux qui partagent un côté en commun, c'est-à-dire que le rayon de l'un est le même rayon de l'autre.
Les angles périgonaux peuvent être constitués d'une série d'angles consécutifs qui, ajoutés ensemble, complètent le 360 °.
Par exemple:
- Deux angles de 180 ° = un angle périgonal
- Trois angles de 120 ° = un angle périgonal
- Quatre angles de 90 ° = un angle périgonal
- Cinq angles de 72 ° = un angle périgonal
- Six angles de 60 ° = un angle périgonal
Et ainsi de suite.
Il est à noter que les angles qui composent le périgonal ne doivent pas forcément avoir la même amplitude.
Par exemple, une série de quatre angles consécutifs qui ont des amplitudes de 30 °, 80 °, 100 ° et 150 ° (360 ° au total) est également un angle périgonal..
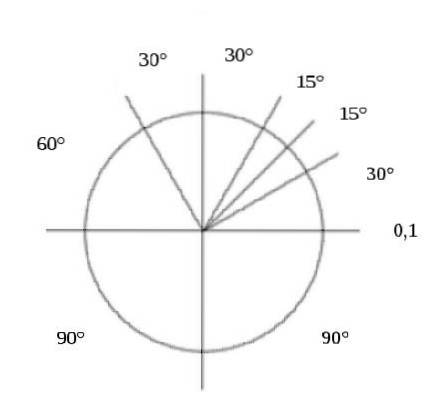
Exemples d'angles périgonaux
Dans notre quotidien, nous sommes entourés d'objets qui mesurent 360 ° et, par conséquent, peuvent être des angles périgonaux. En voici quelques exemples:
1- Les roues
Les roues de bicyclettes, d'automobiles et d'autres véhicules sont des exemples d'angles périgonaux. De plus, les roues des bicyclettes et des automobiles présentent des lignes de division qui pourraient être comprises comme des séries d'angles consécutifs..
2- Une horloge à aiguilles
Les horloges analogiques sont dotées d'aiguilles qui tournent pour marquer l'heure. Prenons en compte une trotteuse et une aiguille des minutes lorsqu'elles sont positionnées sur le numéro 12 de l'horloge, indiquant la première seconde d'une minute..
Les secondes se déplacent à une vitesse de 6 ° par seconde, ce qui signifie qu'après la minute, l'aiguille aura parcouru 360 °.
Dans cet exemple, l'aiguille des minutes et la trotteuse sont les deux rayons d'un angle: l'aiguille des minutes est restée en position, tandis que la trotteuse a fait un tour complet, créant un angle périgonal.
De son côté, une aiguille des minutes met 60 minutes pour réaliser un angle périgonal par rapport à l'aiguille qui marque l'heure..
3- Volants et gouvernails
Les volants d'automobiles et les gouvernails de navires sont également des exemples d'angles périgonaux..
Comme pour une roue de bicyclette, certains volants et gouvernails comportent des segments qui pourraient servir d'angles consécutifs..

4- Les pales d'un ventilateur ou d'un moulin à vent
Ces systèmes comportent généralement trois ou quatre lames. S'il y a trois lames, ce sont trois angles consécutifs de 120 °; s'il en a quatre, ce seront des angles consécutifs de 90 °.
5- Les bobines d'une caméra vidéo
Les bobines d'une caméra vidéo ont trois divisions radiales de 120 ° chacune. Les sommes des angles créés par ces divisions donnent lieu à un angle périgonal.
Les références
- Tournez (géométrie). Récupéré le 2 juin 2017 sur en.wikipedia.org.
- Perigon. Récupéré le 2 juin 2017 de memidex.com.
- Perigon. Récupéré le 2 juin 2017 sur thefreedictionary.com.
- Angle. Récupéré le 2 juin 2017 sur en.wikipedia.org.
- Plein angle. Récupéré le 2 juin 2017 de mathworld.wolfram.com.
- Angles. Récupéré le 2 juin 2017 de mathteacher.com.au.
- Perigon. Récupéré le 2 juin 2017 de merriam-webster.com.
- Perigon. Récupéré le 2 juin 2017 de dictionary.com.


Personne n'a encore commenté ce post.