Les types d'intégrales que nous trouvons dans le calcul sont les intégrales indéfinies et les intégrales définies. Bien que les intégrales définies aient beaucoup plus d'applications que les intégrales indéfinies, il est d'abord nécessaire d'apprendre à résoudre des intégrales indéfinies..
L'une des applications les plus intéressantes des intégrales définies est le calcul du volume d'un solide de révolution. Les deux types d'intégrales ont les mêmes propriétés de linéarité et les techniques d'intégration ne dépendent pas du type d'intégrale.
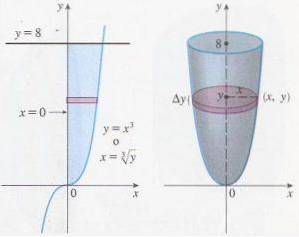
Mais en dépit d'être très similaire, il y a une différence principale; dans le premier type d'intégrale le résultat est une fonction (qui n'est pas spécifique) tandis que dans le second type le résultat est un nombre.
Le monde des intégrales est très large, mais en son sein, nous pouvons distinguer deux types de base d'intégrales, qui ont une grande applicabilité dans la vie quotidienne..
Si F '(x) = f (x) pour tout x dans le domaine de f, on dit que F (x) est une primitive, une primitive ou une intégrale de f (x).
En revanche, observons que (F (x) + C) '= F' (x) = f (x), ce qui implique que l'intégrale d'une fonction n'est pas unique, car donner des valeurs différentes à la constante C nous obtiendrons différentes primitives.
Pour cette raison F (x) + C est appelée l'intégrale indéfinie de f (x) et C est appelée la constante d'intégration et nous l'écrivons comme suit
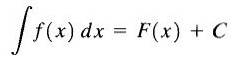
Comme on peut le voir, l'intégrale indéfinie de la fonction f (x) est une famille de fonctions.
Par exemple, si vous voulez calculer l'intégrale indéfinie de la fonction f (x) = 3x², vous devez d'abord trouver une primitive de f (x).
Il est facile de voir que F (x) = x³ est une primitive, puisque F '(x) = 3x². Par conséquent, on peut conclure que
∫f (x) dx = ∫3x²dx = x³ + C.
Soit y = f (x) une fonction réelle et continue sur un intervalle fermé [a, b] et soit F (x) une primitive de f (x). L'intégrale définie de f (x) entre les limites a et b est appelée le nombre F (b) -F (a), et est notée comme suit
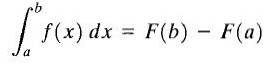
La formule ci-dessus est mieux connue sous le nom de «Théorème fondamental du calcul». Ici, "a" est appelé la limite inférieure et "b" est appelée la limite supérieure. Comme vous pouvez le voir, l'intégrale définie d'une fonction est un nombre.
Dans ce cas, si nous calculons l'intégrale définie de f (x) = 3x² dans l'intervalle [0,3], nous obtiendrons un nombre.
Pour déterminer ce nombre, nous choisissons F (x) = x³ comme primitive de f (x) = 3x². Ensuite, nous calculons F (3) -F (0) ce qui nous donne le résultat 27-0 = 27. En conclusion, l'intégrale définie de f (x) sur l'intervalle [0,3] est 27.
On peut noter que si G (x) = x³ + 3 est choisi, alors G (x) est une primitive de f (x) différente de F (x), mais cela n'affecte pas le résultat puisque G (3) - G (0) = (27 + 3) - (3) = 27. Pour cette raison, dans les intégrales définies, la constante d'intégration n'apparaît pas.
L'une des applications les plus utiles de ce type d'intégrale est qu'elle permet de calculer l'aire (volume) d'une figure plane (d'un solide de révolution), en établissant des fonctions appropriées et des limites d'intégration (et un axe de rotation).
Dans les intégrales définies, nous pouvons en trouver diverses extensions, telles que des intégrales de ligne, des intégrales de surface, des intégrales incorrectes, des intégrales multiples, entre autres, toutes avec des applications très utiles en science et en ingénierie..
Personne n'a encore commenté ce post.