
Solides de révolution volume, types, exercices résolus
le solide de révolution C'est la figure tridimensionnelle qui est générée en faisant tourner une surface plane autour de l'axe axial ou de l'axe de révolution. La figure 1 montre une animation d'un solide de révolution ainsi généré.
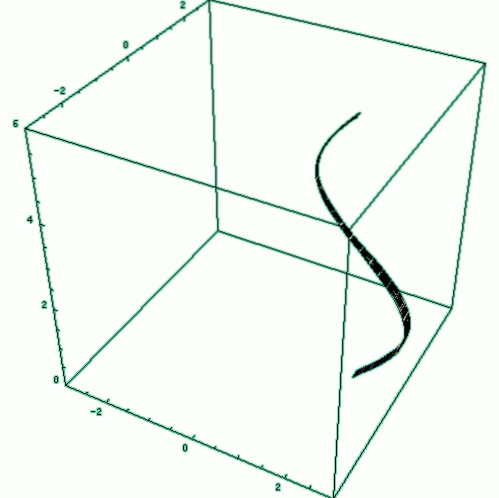
Un autre exemple très facile à visualiser consiste à générer un cylindre circulaire droit, en faisant tourner un rectangle de hauteur ou de longueur h et de rayon r, autour de l'axe x positif (figure 2). Pour trouver son volume, il existe une formule bien connue:
V = aire de la base x hauteur
Les autres solides de révolution sont la sphère, le cône circulaire droit et diverses figures, en fonction de la surface mise en rotation et bien sûr, de l'axe choisi..
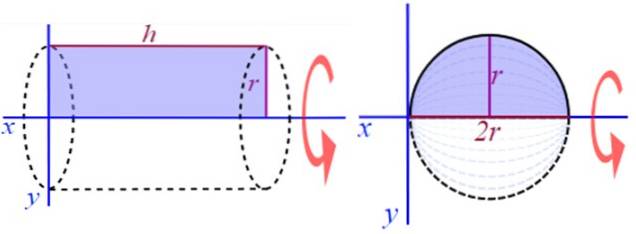
Par exemple, la rotation du demi-cercle autour d'une ligne parallèle au diamètre donne un solide de révolution creuse.
Pour le cylindre, le cône, la sphère, à la fois plein et creux, il existe des formules pour trouver le volume, qui dépend du rayon et de la hauteur. Mais lorsqu'ils sont générés par d'autres surfaces, le volume est calculé par des intégrales définies.
Index des articles
- 1 Types de solides de révolution
- 1.1 Sphère
- 1.2 Cône
- 1.3 Cylindre
- 1.4 Tore
- 2 Méthodes de calcul du volume d'un solide de révolution
- 2.1 Méthode du disque ou de la rondelle
- 2.2 Méthode des couches
- 3 Exercice résolu
- 4 Références
Types de solides de révolution
Les solides de révolution peuvent être classés en fonction de la courbe qui les génère:
Sphère
Il suffit de faire pivoter un demi-cercle autour d'un axe qui sera le diamètre de la sphère de rayon R. Son volume est:
Vsphère = (4/3) πR3
Cône
Pour obtenir un cône de hauteur H et de rayon R, la surface à faire tourner est un triangle rectangle, autour de l'axe axial qui passe par l'une des jambes. Son volume est:
Vcône = (1/3) πHRdeux
Cylindre
En faisant tourner un rectangle autour d'un axe axial qui passe par l'un des côtés, qui peut être le côté court ou le côté long, on obtient un cylindre circulaire droit de rayon R et de hauteur H, dont le volume est:
Vcylindre = πRdeuxH
Tore
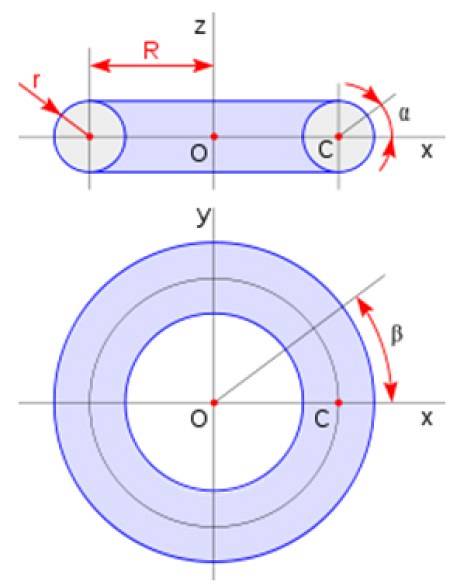
Le tore a la forme d'un beignet. Il est obtenu en faisant tourner une région circulaire autour d'une ligne dans le plan qui ne coupe pas le cercle. Son volume est donné par:
Vtorus = 2πadeuxR
Où a est le rayon de la section transversale et R est le rayon du tore selon le schéma présenté dans la figure:
Méthodes de calcul du volume d'un solide de révolution
En calcul intégral, ces deux méthodes sont fréquentes:
-Disques et rondelles
-Coquilles
Méthode de disque ou de rondelle
Lors du tranchage d'un solide de révolution, la section transversale peut être un disque, si le solide est solide, ou elle peut être une sorte de rondelle (un disque avec un trou au milieu), s'il s'agit d'un solide creux..
Supposons qu'une région plane pivote autour de l'axe horizontal. De cette région plate, nous prenons un petit rectangle de largeur Δx, qui est tourné perpendiculairement autour de l'axe axial.
La hauteur du rectangle se situe entre la courbe la plus externe R (x) et la courbe la plus interne r (x). Ils correspondent respectivement au rayon extérieur et au rayon intérieur..
En effectuant cette rotation, une rondelle de volume ΔV est générée, donnée par:
ΔV = volume complet - volume du trou (le cas échéant)
En se rappelant que le volume d'un cylindre circulaire droit est π. radiodeux x hauteur, nous avons:
ΔV = π [Rdeux(x) - rdeux(x)] Δx
Le solide peut être divisé en une multitude de petits volumes ΔV. Si nous les ajoutons tous, nous aurons le volume complet.
Pour ce faire, on fait tendre le volume ΔV à 0, avec lequel Δx devient également très petit, devenant un différentiel dx.
Nous avons donc une intégrale:
V = ∫àb π [Rdeux(x) - rdeux(x)] dx
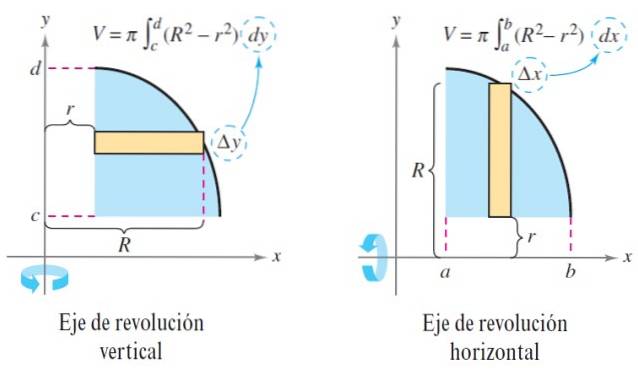
Dans le cas où le solide est solide, alors la fonction r (x) = 0, la tranche du solide qui est générée est un disque et le volume reste:
V = ∫àb πRdeux(x) dx
Lorsque l'axe de révolution est vertical, les équations ci-dessus prennent la forme:
V = ∫àb π [Rdeux (y) - rdeux (y)] dy y V = ∫àb πRdeux(y) dy
Méthode de couche
Comme son nom l'indique, cette méthode consiste à supposer que le solide est constitué de couches d'épaisseur différentielle. La couche est un tube mince qui provient de la rotation d'un rectangle parallèle à l'axe de rotation.
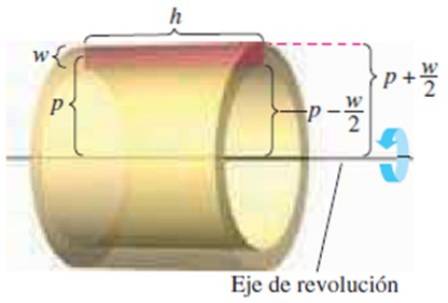
Nous avons les dimensions suivantes:
-La hauteur du rectangle w
-Sa longitude h
-La distance entre le centre du rectangle et l'axe de rotation p
Sachant que le volume de la couche est volume extérieur - volume intérieur:
π (p + w / 2)deuxh - π (p - w / 2)deuxh
En développant des produits remarquables et en les simplifiant, vous obtenez:
Volume de couche = 2π⋅p⋅w⋅h
Faisons maintenant la hauteur w du rectangle Δy, comme le montre la figure suivante:
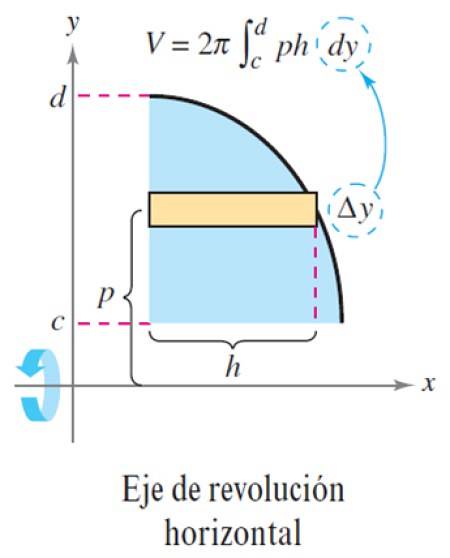
Avec cela, le volume ΔV est:
ΔV = 2π p x h x Δy
Et faire le nombre de couches n est très grand, Δy devient un dy différentiel, dont le volume total est l'intégrale:
V = ∫cré 2π p (y) h (y) dy
La procédure décrite s'applique de la même manière lorsque l'axe de révolution est vertical:
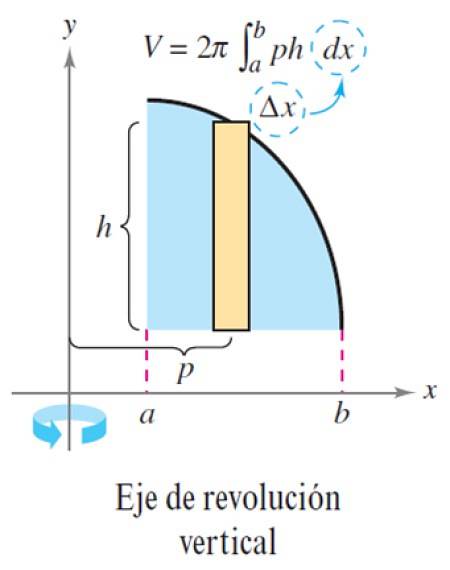
Exercice résolu
Trouvez le volume généré par la rotation de la région plane entre les courbes:
y = xdeux; y = 0; x = 2
Autour de l'axe y.
Solution
-La première chose que nous devons faire est de représenter graphiquement la région qui générera le solide de révolution et indiquera l'axe de rotation. Nous l'avons dans le graphique suivant:
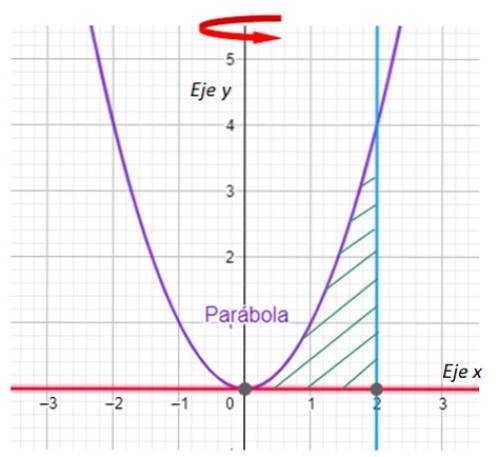
-Nous recherchons maintenant les intersections entre la courbe y = xdeux et la ligne x = 2. Pour sa part, la ligne y = 0 n'est autre que l'axe des x.
À partir du graphique, il est facile de voir que la parabole et la droite se coupent au point (2,4), ce qui est corroboré en remplaçant x = 2 dans y = xdeux.
-Ensuite, l'une des méthodes de calcul du volume est choisie, par exemple la méthode des couches avec axe vertical de révolution:
V = ∫àb 2π p (x) h (x) dx
Étape 1: dessinez le rectangle
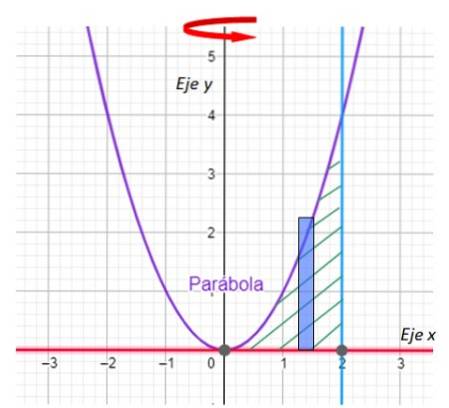
Important: Dans la méthode de stratification, le côté long du rectangle est parallèle à l'axe de rotation.
Étape 2: déterminer p (x)
Le rayon du calque est X
Étape 3: déterminer h (x)
La hauteur du rectangle est déterminée par la parabole xdeux.
Étape 4: établir et résoudre l'intégrale de volume
La variable d'intégration est x, qui varie entre 0 et 2, avec cela nous avons les limites de l'intégration. Substituer les expressions pour p (x) et h (x)

Les références
- Larson, R. 2010. Calcul d'une variable. 9ème. Édition. Mcgraw Hill.
- Purcell, E. 2007. Calcul avec géométrie analytique. 9ème. Édition. Éducation Pearson.
- Wikipédia. Solide de révolution. Récupéré de: en.wikipedia.org.
- Wikipédia. Tore Récupéré de: es.wikipedia.org.
- Wolfram MathWorld. Solide de révolution. Récupéré de: mathworld.wolfram.com.



Personne n'a encore commenté ce post.