
Sommation télescopique comment elle est résolue et les exercices sont résolus

La addition télescopique est une branche d'opérations avec des séries de nombres. Adresse la somme des éléments d'une valeur initiale à "n" d'expressions dont l'argument obéit à l'un des modèles suivants:
(FX - Fx + 1); (Fx + 1 - FX)
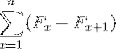
Comme aussi:
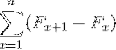

Ils représentent une somme d'éléments qui, lorsqu'ils sont développés, sont soumis à des annulations de termes opposés. Permettant de définir l'égalité suivante pour les sommations télescopiques:
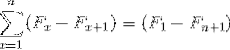
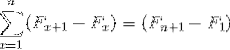
Son nom vient de la relation avec l'apparition d'un télescope classique, qui pourrait être plié et déplié, modifiant notamment sa dimension. De la même manière, les sommations télescopiques, de nature infinie, peuvent être résumées dans l'expression simplifiée:
F1 - Fn + 1
Index des articles
- 1 démo
- 2 Comment résoudre?
- 2.1 Décomposition en fractions simples
- 3 Histoire
- 4 exercices
- 4.1 Exercice 1
- 4.2 Exercice 2
- 5 Références
Manifestation
Lors de l'élaboration de la sommation des termes, l'élimination des facteurs est assez évidente. Où pour chacun des cas, les éléments opposés apparaîtront dans la prochaine itération.
Le premier cas, (FX - Fx + 1), puisque le processus fonctionne de manière homologue pour (Fx + 1-FX).
En développant les 3 premières valeurs 1, 2, 3 la tendance à la simplification est observée
X1 (F1 - F1 + 1) = F1 - Fdeux
Xdeux (Fdeux - F2 + 1) = Fdeux - F3
X3 (F3 - F3 + 1) = F3 - F4
Où lors de l'expression de la somme des éléments décrits:
X1 + Xdeux + X3 = F1 - Fdeux + Fdeux - F3 + F3 - F4
On observe que les termes Fdeux et F3 ils sont décrits avec leurs opposés, ce qui rend leur simplification inévitable. De la même manière, on observe que les termes F1 et F4 se maintiennent.
Si la somme a été faite de x = 1 à x = 3, cela signifie que l'élément F4 correspond au terme générique Fn + 1.
Démontrant ainsi l'égalité:
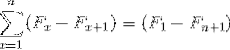
Comment est-ce résolu?
Le but des sommations télescopiques est de faciliter le travail, de sorte qu'il ne soit pas nécessaire de développer un nombre infini de termes, ou de simplifier une chaîne d'additifs trop longue.
Pour sa résolution, il suffira d'évaluer les termes F1 et Fn + 1. Ces substitutions simples constituent le résultat final de la sommation.
La totalité des termes ne sera pas exprimée, devenant nécessaire uniquement pour la démonstration du résultat, mais pas pour le processus de calcul normal.
L'important est de remarquer la convergence des séries numériques. Parfois, l'argument de sommation ne sera pas exprimé de manière télescopique. Dans ces cas, la mise en œuvre de méthodes d'affacturage alternatives est très courante..
La méthode de factorisation caractéristique des additions télescopiques est celle des fractions simples. Cela se produit lorsqu'une fraction d'origine est décomposée en une somme de plusieurs fractions, où le motif télescopique (FX - Fx + 1) ou (Fx + 1 - FX).
Décomposition en fractions simples
Pour vérifier la convergence des séries numériques, il est très courant de transformer des expressions rationnelles avec la méthode des fractions simples. Le but est de modéliser l'intrigue sous la forme d'une sommation télescopique..
Par exemple, l'égalité suivante représente une décomposition en fractions simples:
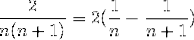
Lors du développement de la série de nombres et de l'application des propriétés correspondantes, l'expression prend la forme suivante:
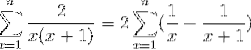
Où la forme télescopique (FX - Fx + 1).
La procédure est assez intuitive et consiste à trouver les valeurs du numérateur qui, sans casser l'égalité, permettent de séparer les produits qui sont dans le dénominateur. Les équations qui se posent dans la détermination de ces valeurs, sont soulevées selon des comparaisons entre les deux côtés de l'égalité.
Cette procédure est observée étape par étape dans le développement de l'exercice 2.
Histoire
Il est assez incertain de pouvoir définir le moment historique dans lequel les sommations télescopiques ont été présentées. Cependant, sa mise en œuvre commence à être vue au XVIIe siècle, dans les études de séries numériques menées par Leibniz et Huygens..
Les deux mathématiciens, explorant les sommations des nombres triangulaires, commencent à remarquer des tendances dans la convergence de certaines séries d'éléments successifs. Mais encore plus intéressant est le début de la modélisation de ces expressions, dans des éléments qui ne se succèdent pas forcément.
En fait, l'expression utilisée précédemment pour désigner des fractions simples:
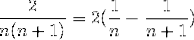
Il a été présenté par Huygens et a immédiatement attiré l'attention de Leibniz. Qui au fil du temps a pu observer la convergence vers la valeur 2. Sans le savoir, il a implémenté le format de sommation télescopique.
Exercices
Exercice 1
Définissez vers quel terme converge la somme suivante:
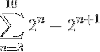
Lors du développement manuel de la somme, le modèle suivant est observé:
(deux3 - deux4) + (24 - deux5) + (25 - deux6)… (deuxdix - deuxOnze)
Où les facteurs de 24 jusqu'à 2dix Ils présentent des parties positives et négatives, rendant leur annulation évidente. Ensuite, les seuls facteurs qui ne seront pas simplifiés seront les premiers "23"Et le dernier" 2Onze".
De cette manière, lors de la mise en œuvre du critère de sommation télescopique, on obtient:
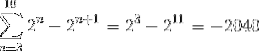
Exercice 2
Transformez l'argument en une sommation de type télescopique et définissez la convergence de la série:
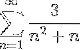
Comme indiqué dans l'énoncé, la première chose à faire sera de décomposer en fractions simples, afin de reformuler l'argument et de l'exprimer de manière télescopique..
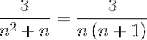
Vous devez trouver 2 fractions dont les dénominateurs sont respectivement "n" et "n + 1", où la méthode utilisée ci-dessous doit obtenir les valeurs du numérateur qui répondent à l'égalité.
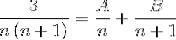
Nous procédons à la définition des valeurs de A et B.D'abord, ajoutons les fractions.
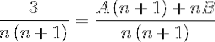
Ensuite, les dénominateurs sont simplifiés et une équation linéaire est établie.
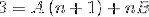
Dans l'étape suivante, l'expression à droite est utilisée, jusqu'à ce qu'un motif comparable au «3» à gauche soit obtenu..
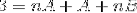
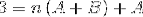
Pour définir les équations à utiliser, les résultats des deux côtés de l'égalité doivent être comparés. Autrement dit, aucune valeur de la variable n n'est observée sur le côté gauche, de cette manière A + B devra être égal à zéro.
A + B = 0; A = -B
Par contre, la valeur constante A devra être égale à la valeur constante 3.
A = 3
Donc.
A = 3 et B = -3
Une fois que les valeurs du numérateur pour les fractions simples ont déjà été définies, la sommation est reformulée.
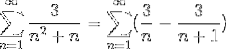
Où la forme générique de sommation télescopique a déjà été réalisée. La série télescopique est développée.
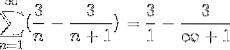
Où, en divisant par un très grand nombre, le résultat se rapprochera de plus en plus de zéro, en observant la convergence de la série vers la valeur 3.
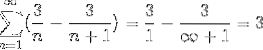
Ce type de série ne pouvait être résolu d'aucune autre manière, en raison du nombre infini d'itérations qui définissent le problème. Cependant, cette méthode, avec beaucoup d'autres, encadre la branche d'étude des séries numériques, dont l'objectif est de déterminer les valeurs de convergence ou de définir la divergence de ces séries..
Les références
- Cours de calcul infinitésimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. ÉDITUM, 1994.
- Calcul intégral: séquences et séries de fonctions. Antonio Rivera Figueroa. Grupo Editorial Patria, 21 octobre. 2014.
- Un cours de calcul et d'analyse réelle. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 juin. 2006.
- Série infinie. Tomlinson Fort. La presse Clarendon, 1930.
- Éléments de la théorie des processus infinis. Lloyd Leroy Smail. McGraw-Hill Book Company, constituée en société, 1923.


Personne n'a encore commenté ce post.