
Taux marginal de substitution comment il est calculé et exemple

La taux marginal de substitution (TMS) est la quantité d'un produit que le consommateur est prêt à abandonner pour un autre produit, à condition que le nouveau bien soit satisfaisant de la même manière. Il est utilisé dans la théorie de l'indifférence pour étudier le comportement des consommateurs.
Il peut être défini comme le nombre d'unités d'un produit X qu'il faut abandonner pour obtenir une unité supplémentaire d'un produit Y, tout en conservant le même niveau d'utilité ou de satisfaction. Par conséquent, il implique l'échange de marchandises pour modifier l'attribution des produits combinés dans différents emballages.

Une courbe d'indifférence est un graphique des différents emballages de deux produits qu'un consommateur est indifférent à choisir. Autrement dit, il n'a aucune préférence pour un package par rapport à un autre.
Si les unités d'un produit sont diminuées, le consommateur doit être compensé avec plus d'unités de l'autre produit pour maintenir la condition d'indifférence. Le taux marginal de substitution est le taux auquel une diminution d'un produit doit être compensée par une augmentation de l'autre produit..
Index des articles
- 1 Quel est le taux marginal de substitution?
- 1.1 Principe de diminution du taux marginal de substitution
- 1.2 Limitations
- 2 Comment est-il calculé?
- 2.1 Formule
- 3 Exemple
- 4 Références
Quel est le taux marginal de substitution?
Le taux marginal de substitution est un terme économique qui désigne le point auquel un produit est substituable à un autre..
Ce taux forme une courbe descendante, appelée courbe d'indifférence. Chaque point le long de celui-ci représente les quantités de produit X et de produit Y qui conviendraient de se substituer l'une à l'autre..
Il change toujours pour un point donné sur la courbe, représentant mathématiquement la pente de la courbe à ce point. En tout point donné le long d'une courbe d'indifférence, le taux marginal de substitution est la pente de la courbe d'indifférence en ce point..
Si le taux marginal de substitution de X par Y ou Y par X diminue, la courbe d'indifférence doit être convexe à l'origine.
Par contre, si elle est constante, la courbe d'indifférence sera une ligne droite descendant vers la droite d'un angle de 45 ° pour chaque axe. Si le taux marginal de substitution augmente, la courbe d'indifférence sera concave à l'origine.
Principe de diminution du taux marginal de substitution
Le TMS du produit X par rapport au produit Y diminue au fur et à mesure que le produit X est remplacé par le produit Y. En d'autres termes, comme le consommateur a de plus en plus de produit X, il sera prêt à abandonner de moins en moins de produit. Y.
La vitesse à laquelle le consommateur substitue le produit X au produit Y est plus élevée au début. Cependant, à mesure que le processus de substitution se poursuit, le taux de substitution commence à baisser..
Limites
Le taux marginal de substitution n'examine pas la combinaison de produits qu'un consommateur préférerait plus ou moins qu'un autre mélange, mais examine plutôt quelles combinaisons de produits le consommateur aimerait avoir la même chose..
Il n'explore pas non plus l'utilité marginale, c'est-à-dire dans quelle mesure un consommateur serait meilleur ou pire avec une combinaison de produits plutôt qu'une autre, car le long de la courbe d'indifférence, toutes les combinaisons de produits sont évaluées de la même manière par le consommateur..
Comment est-il calculé?
La loi de l'utilité marginale décroissante stipule que l'utilité marginale, qui est l'utilité supplémentaire pour chaque nouvelle unité d'un produit, sera inférieure à l'utilité marginale de l'unité précédente..
Autrement dit, la première unité d'un produit a l'utilité la plus élevée, la seconde unité a la deuxième utilité la plus élevée, et ainsi de suite..
Or, si un consommateur substitue un produit X à un autre produit Y, il doit être compensé avec le plus grand nombre d'unités de Y pour la première unité de X, le deuxième plus grand nombre d'unités de Y pour la deuxième unité de X, et ainsi allumé en continu..
Cela montre que le taux marginal de substitution change continuellement au fur et à mesure que l'on évolue le long d'une courbe d'indifférence..
Pour de très petits changements dans un produit, le taux marginal de substitution se rapproche de la pente de la courbe d'indifférence, qui est égale à la variation de Y divisée par la variation de X.
Formule
Le taux marginal de substitution (TMS) est calculé entre deux produits placés sur une courbe d'indifférence, montrant un point d'utilité égale pour chaque combinaison de «produit X» et de «produit Y». La formule du taux marginal de substitution est:
TMSxy = - (Y1 - Y0) / (X1 - X0) = dy / dx, où:
- «X» et «Y» représentent chacun un produit différent.
- dy / dx fait référence à la dérivée de y par rapport à x.
En revanche, TMSxy et TMSyx ne sont pas les mêmes. En fait, ils sont réciproques l'un de l'autre, c'est-à-dire TMSyx = 1 / TMSxy.
On peut montrer que le taux marginal de substitution de y pour x est égal au prix de x divisé par y. Ceci est égal à l'utilité marginale de x divisée par l'utilité marginale de y, c'est-à-dire TMSxy = MUx / MUy
La courbe d'indifférence devient plus horizontale à mesure qu'elle passe de l'axe des y à l'axe des x. C'est parce que lorsque y devient rare et que x devient abondant, le taux marginal de substitution de x avec y diminue. C'est ce qu'on appelle le taux marginal décroissant de substitution..
Exemple
Par exemple, un consommateur doit choisir entre des hamburgers et des hot dogs. Pour déterminer le taux marginal de substitution, on demande au consommateur quelles combinaisons de hamburgers et de hot-dogs offrent le même niveau de satisfaction..
Lorsque ces combinaisons sont représentées graphiquement, la pente de la ligne résultante est négative..
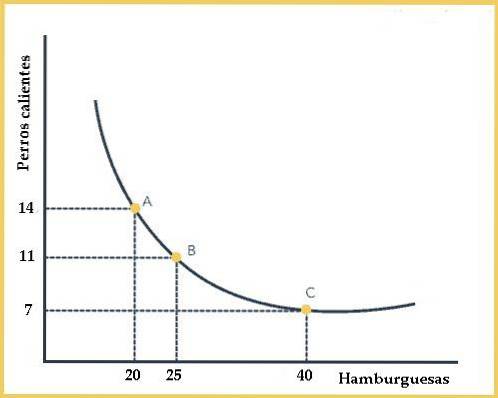
Cela signifie que le consommateur est confronté à un taux de substitution marginal décroissant. Tant que vous avez plus de hamburgers que de hot-dogs, le consommateur sera prêt à abandonner moins de hot-dogs pour plus de hamburgers..
Dans le graphique, au point A, on peut voir que le consommateur est prêt à remplacer (14-11) = 3 unités de hot-dogs pour (25-20) = 5 unités supplémentaires de hamburgers. Par conséquent, à ce stade, le taux marginal de substitution des hot dogs par les hamburgers du consommateur est de 5/3 = 1,67.
Cependant, au point B, le consommateur pour remplacer autre (11-7) = 4 unités de hot-dogs aurait besoin de (40-25) = 15 unités supplémentaires de hamburgers, étant à ce stade son TMS de 15/4 = 3, 75.
On suppose que l'une des trois combinaisons du graphique a le même niveau d'utilité.
Les références
- Adam Hayes (2019). Taux marginal de substitution - Définition MRS. Investopedia. Tiré de: investopedia.com.
- Prateek Agarwal (2018). Taux marginal de substitution. Économiste intelligent. Tiré de: intelligenteconomist.com.
- Jan Obaidullah (2018). Taux marginal de substitution. Xplaind. Tiré de: xplaind.com.
- Smriti Chand (2019). Le taux marginal de substitution (MRS) | Économie. Votre bibliothèque d'articles. Tiré de: yourarticlelibrary.com.
- Toppr (2019). Taux marginal de substitution. Tiré de: toppr.com.


Personne n'a encore commenté ce post.