
Théorème de Thévenin en quoi il consiste, applications et exemples
le Théorème de Thévenin indique qu'un circuit avec les bornes A et B peut être remplacé par un circuit équivalent composé d'une source et d'une résistance série, dont les valeurs donnent la même différence de potentiel entre A et B et la même impédance que le circuit d'origine.
Ce théorème a été fait connaître en 1883 par l'ingénieur français Léon Charles Thévenin, mais on prétend qu'il a été énoncé trente ans plus tôt par le physicien allemand Hermann von Helmholtz.

Son utilité réside dans le fait que, même lorsque le circuit d'origine est complexe ou inconnu, aux fins d'une charge ou d'une impédance placée entre les bornes A et B, le circuit équivalent Thévenin simple se comporte de la même manière que l'original..
Index des articles
- 1 Comment calculer la tension équivalente étape par étape?
- 1.1 - Expérimentalement
- 1.2 - Résoudre le circuit
- 2 Applications du théorème de Thévenin (partie I)
- 2.1 Exemple 1a (calcul de la tension équivalente pas à pas)
- 2.2 Exemple 1b (courant dans la charge utilisant l'équivalent Thévenin)
- 3 Preuve du théorème de Thévenin
- 4 Application du théorème de Thévenin (partie II)
- 4.1 Exemple 2a (résistance équivalente au Thévenin)
- 4.2 Exemple 2b
- 4.3 Exemple 2c
- 5 Application du théorème de Thévenin (partie III)
- 5.1 Exemple 3
- 6 Références
Comment calculer la tension équivalente étape par étape?
La tension ou la différence de potentiel du circuit équivalent peut être obtenue des manières suivantes:
- Expérimentalement
Obtention de la tension Thévenin équivalente
S'il s'agit d'un appareil ou d'un équipement qui se trouve dans une «boîte noire», la différence de potentiel entre les bornes A et B est mesurée avec un voltmètre ou un oscilloscope. Il est très important qu'aucune charge ou impédance ne soit placée entre les bornes A et B.
Un voltmètre ou un oscilloscope ne représente aucune charge sur les bornes, puisque les deux appareils ont une très grande impédance (idéalement infinie) et ce serait comme si les bornes A et B étaient sans charge. La tension ou tension ainsi obtenue est la tension équivalente Thévenin.
Obtention de l'impédance équivalente Thévenin
Pour obtenir l'impédance équivalente à partir d'une mesure expérimentale, une résistance connue est placée entre les bornes A et B et la chute de tension ou le signal de tension est mesuré avec un oscilloscope..
À partir de la chute de tension dans la résistance connue entre les bornes, le courant qui la traverse peut être obtenu.
Le produit du courant obtenu avec la résistance équivalente plus la chute de tension mesurée dans la résistance connue est égal à la tension Thévenin équivalente obtenue précédemment. A partir de cette égalité, l'impédance Thévenin équivalente est effacée.
- Résoudre le circuit
Calcul de la tension équivalente Thévenin
Tout d'abord, toute charge ou impédance est déconnectée des bornes A et B.
Comme le circuit est connu, la théorie du maillage ou les lois de Kirchhoff sont appliquées pour trouver la tension aux bornes. Cette tension sera l'équivalent de Thévenin.
Calcul de l'impédance équivalente Thévenin
Pour obtenir l'impédance équivalente, nous procédons à:
- Remplacez les sources de tension du circuit d'origine par des courts-circuits «impédance nulle» et les sources de courant du circuit d'origine par des sources ouvertes «impédance infinie».
- Ensuite, l'impédance équivalente est calculée en suivant les règles des impédances série et des impédances parallèles.
Applications du théorème de Thévenin (partie I)
Nous appliquerons le théorème de Thévenin pour résoudre certains circuits. Dans cette première partie on considère un circuit qui ne possède que des sources de tension et des résistances.
Exemple 1a (calcul de la contrainte équivalente étape par étape)
La figure 2 montre le circuit qui est dans une boîte céleste qui a deux batteries de force électromotrice V1 et V2 respectivement et des résistances R1 et R2, le circuit a des bornes A et B dans lesquelles une charge peut être connectée.
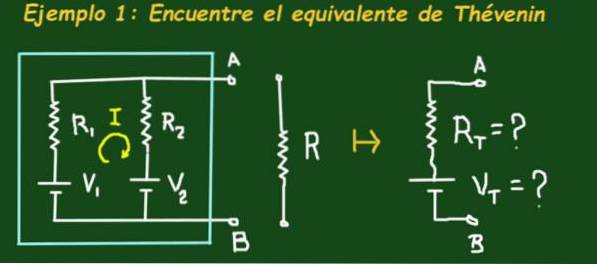
Le but est de trouver le circuit équivalent de Thévenin, c'est-à-dire de déterminer les valeurs Vt et Rt du circuit équivalent. Appliquez les valeurs suivantes: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω et R = 1Ω.
Solution étape par étape
Étape 1
Nous déterminerons la tension aux bornes A et B lorsqu'aucune charge n'y est placée.
Étape 2
Le circuit à résoudre est constitué d'une seule maille à travers laquelle circule un courant I que nous avons pris positif dans le sens des aiguilles d'une montre.
Étape 3
Nous parcourons le maillage en commençant par le coin inférieur gauche. Le chemin mène à l'équation suivante:
V1 - I * R1 - I * R2 - V2 = 0
Étape 4
Nous résolvons le courant de maillage I et obtenons:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Étape 5
Avec le courant de maillage, nous pouvons déterminer la différence de tension entre A et B, qui est:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Autrement dit, la tension équivalente à Thevenin est: Vt = 3V.
Étape 6 (résistance équivalente au Thévenin)
On procède maintenant au calcul de la résistance équivalente Thévenin, pour laquelle et comme mentionné précédemment, les sources de tension sont remplacées par un câble.
Dans ce cas, nous n'avons que deux résistances en parallèle, donc la résistance équivalente Thévenin est:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Exemple 1b (courant dans la charge utilisant l'équivalent Thévenin)
Connectez en tant que charge aux bornes A et B une résistance R = 1Ω au circuit équivalent et trouvez le courant qui traverse ladite charge.
Solution
Lorsque la résistance R est connectée au circuit équivalent de Thevenin, on a un circuit simple qui consiste en une source Vt une résistance Rt en série avec la résistance R.
Nous appellerons Ic le courant qui traverse la charge R, de sorte que l'équation de maillage ressemble à ceci:
Vt - Ic * Rt - Ic * R = 0
d'où il résulte que Ic est donné par:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A
Preuve du théorème de Thévenin
Pour vérifier que le théorème de Thévenin est vrai, connectez R au circuit d'origine et trouvez le courant traversant R en appliquant la loi de maillage au circuit résultant.
Le circuit résultant reste et ses équations de maillage restent comme indiqué dans la figure suivante:
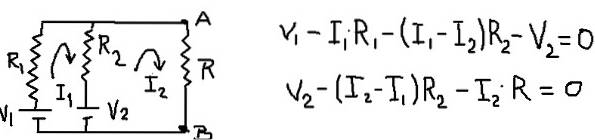
En ajoutant les équations de maillage, il est possible de trouver le courant de maillage I1 en fonction du courant I2. Ensuite, il est remplacé dans la deuxième équation de maillage et une équation est laissée avec I2 comme seule inconnue. Le tableau suivant montre les opérations.
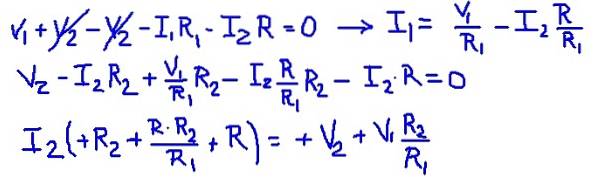
Ensuite, les valeurs de la résistance et des tensions des sources sont substituées, obtenant la valeur numérique du courant de maillage I2.

Le courant de maillage I2 est le courant qui traverse la résistance de charge R et la valeur trouvée de 1 A coïncide parfaitement avec celle trouvée précédemment avec le circuit Thévenin équivalent..
Application du théorème de Thévenin (partie II)
Dans cette seconde partie, le théorème de Thévenin sera appliqué dans un circuit qui a des sources de tension, source de courant et résistances.
Exemple 2a (résistance équivalente au Thévenin)
L'objectif est de déterminer le circuit équivalent Thévenin correspondant au circuit de la figure suivante, lorsque les bornes sont sans résistance de 1 ohm, alors la résistance est placée et le courant qui le traverse est déterminé.
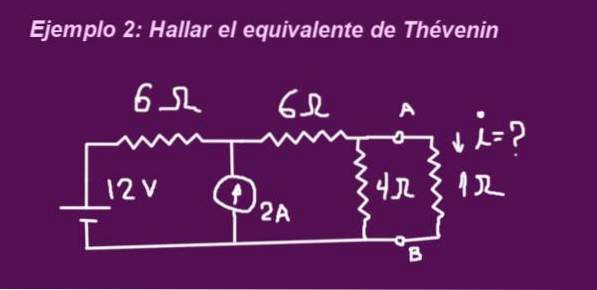
Solution
Pour trouver la résistance équivalente, supprimez la résistance de charge (dans ce cas le 1 ohm). De plus, les sources de tension sont remplacées par un court-circuit et les sources de courant par un circuit ouvert..
De cette manière, le circuit pour lequel la résistance équivalente sera calculée est celui illustré ci-dessous:
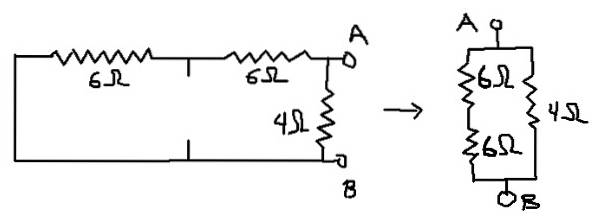
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω qui est la résistance équivalente à Thevenin (Rth).
Exemple 2b
Calculer la tension équivalente Thévenin.
Solution
Pour calculer la tension équivalente Thévenin, nous considérons le circuit suivant, dans lequel nous placerons les courants dans I1 et I2 dans les branches indiquées dans la figure suivante:
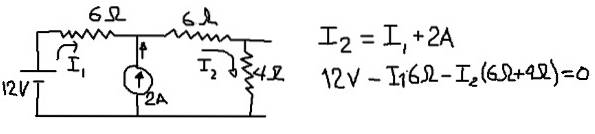
La figure précédente montre l'équation des nœuds courants et l'équation des tensions lorsque le maillage externe est parcouru. A partir de la seconde des équations, le courant I1 est effacé:
I1 = 2 - I2 * (5/3)
Cette équation est substituée dans l'équation des nœuds:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Cela signifie que la chute de tension aux bornes de la résistance de 4 ohms est de 6 volts..
En bref, la tension Thévenin est Vth = 6 V.
Exemple 2c
Recherche du circuit équivalent Thevenin et du courant dans la résistance de charge.
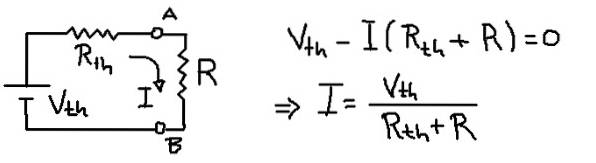
Solution
La figure précédente montre le circuit équivalent Thévenin avec la résistance de charge R. De l'équation de tension dans le maillage, on déduit le courant I qui traverse la résistance de charge R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Application du théorème de Thévenin (partie III)
Dans cette troisième partie de l'application du théorème de Thévenin, on considère un circuit de courant alternatif contenant une source de tension alternative, un condensateur, une inductance et une résistance..
Exemple 3
Le but est de trouver le Circuit Thévenin équivalent au circuit suivant:
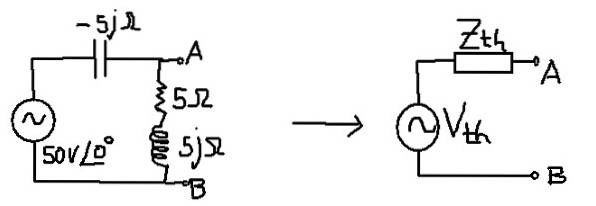
Solution
L'impédance équivalente correspond à celle du condensateur en parallèle avec la combinaison série de la résistance et de l'inductance.
L'inverse de l'impédance équivalente est donnée par:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Et l'impédance équivalente sera alors:
Zeq = (1 - 3 j) Ohm
Le courant complexe I peut être dérivé de l'équation de maillage:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
On calcule maintenant la chute de tension dans la résistance plus l'inductance, c'est-à-dire la tension Vab qui sera la tension Thévenin équivalente:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
En d'autres termes, la tension équivalente a la même valeur de crête que la source d'origine mais est déphasée de 45 degrés: Vth = 50V∠45º
Les références
- Tutoriels électroniques, théorème de Thevenin. Récupéré de: electronics-tutorials.ws
- Questions et réponses sur la théorie des réseaux. Théorème de Thevenin. Récupéré de: sanfoundry.com
- Théorème de Thevenin. Procédure étape par étape. Récupéré de: electrictechnology.org
- Théorème de Thevenin. Exemple résolu étape par étape. Récupéré de: electricsimple.blogspot.com
- Atelier sur les théorèmes de Thevenin et Norton. Récupéré de: web.iit.edu
- Wikipédia. Théorème de Thévenin. Récupéré de: wikipedia.com

Personne n'a encore commenté ce post.