
Propriétés de la transformée de Fourier, applications, exemples
La Transformée de Fourier est une méthode d'adéquation analytique orientée vers des fonctions intégrables appartenant à la famille des tintégralement transformé. Il consiste en une redéfinition des fonctions F (t) en termes de Cos (t) et Sen (t).
Les identités trigonométriques de ces fonctions, ainsi que leurs caractéristiques de dérivation et d'antidérivation, servent à définir la transformée de Fourier à travers la fonction complexe suivante:
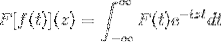
Ce qui est vrai tant que l'expression a du sens, c'est-à-dire lorsque l'intégrale impropre est convergente. On dit algébriquement la transformée de Fourier comme un homéomorphisme linéaire.
Chaque fonction qui peut être utilisée avec une transformée de Fourier doit présenter null en dehors d'un paramètre défini.
Index des articles
- 1 Propriétés
- 1.1 Existence
- 1.2 Linéarité de la transformation de Fourier
- 1.3 Transformée de Fourier d'un dérivé
- 1.4 Différenciation de la transformée de Fourier
- 1.5 Transformée de Fourier d'une traduction
- 1.6 Traduction de la transformée de Fourier
- 1.7 Transformée de Fourier d'un groupe d'échelle
- 1.8 Symétrie
- 1.9 Transformée de Fourier d'un produit de convolution
- 1.10 Continuité et décroissance à l'infini
- 2 Histoire
- 3 À quoi sert la transformée de Fourier?
- 3.1 La série de Fourier
- 3.2 Autres formes de la série de Fourier
- 4 applications
- 4.1 Calcul de la solution fondamentale
- 4.2 Théorie du signal
- 5 exemples
- 5.1 Exemple 1
- 5.2 Exemple 2
- 6 Exercices proposés
- 7 Références
Propriétés

La transformée de Fourier répond aux propriétés suivantes:
Existence
Vérifier l'existence de la transformée de Fourier dans une fonction f (t) définie dans les réels R, les 2 axiomes suivants doivent être remplis:
- f (t) est continue par morceaux pour tout R
- f (t) est intégrable dans R
Linéarité de la transformation de Fourier
Soit M (t) et N (t) deux fonctions quelconques avec des transformées de Fourier définies, avec toutes les constantes a et b.
F [a M (t) + b N (t)] (z) = a F [M (t)] (z) + b F [N (t)] (z)
Ce qui est également soutenu par la linéarité de l'intégrale du même nom.
Transformée de Fourier d'un dérivé
Il a une fonction F qui est continue et intégrable dans tous les réels, où:
Et le dérivé de f (f ') est continue et définie au coup par coup tout au long R
La transformée de Fourier d'un dérivé est définie par intégration par parties, par l'expression suivante:
F [f '(t)] (z) = izF [f (t)] (z)
Dans les dérivations d'ordre supérieur, il sera appliqué de manière homologue, où pour tout n 1 nous avons:
F [F n'(t)] (z) = (iz)nF [f (t)] (z)
Différenciation de la transformée de Fourier
Il a une fonction F qui est continue et intégrable dans tous les réels, où:
i (d / dz)F [f (t)] (z) = F [t. f (t)] (z)
Transformée de Fourier d'une traduction
Pour tout θ qui appartient à un ensemble S et T qui appartient à l'ensemble S ', on a:
F [ τà θ] = et-iay F [ θ] F [ τàT ] = et-iax F [ T]
Avec τà travaillant comme opérateur de traduction sur le vecteur a.
Traduction de la transformée de Fourier
Pour tout θ qui appartient à un ensemble S et T qui appartient à l'ensemble S ', on a:
τà F [θ] = F [et-iax.θ] τà F [T ] = F [et-iay . T]
Pour tout à qui appartient à R
Transformée de Fourier d'un groupe d'échelle
Pour tout θ qui appartient à un ensemble S. T qui appartient à l'ensemble S '
λ appartenant à R - 0 il faut que:
F [θ (λx)] = (1 / | λ |) F [θ] (O /λ)
F [T (λx)] = (1 / | λ |) F [T] (y / λ)
Oui F est une fonction continue et clairement intégrable, où a> 0. Alors:
F [f (at)] (z) = (1 / a) F [f (t)] (z / a)
Pour démontrer ce résultat, nous pouvons procéder au changement de variable.
Lorsque T → + alors s = à → + ∞
Lorsque T → - alors s = à → - ∞
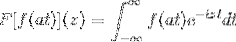
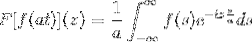
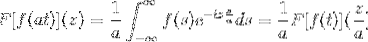
Symétrie
Pour étudier la symétrie de la transformée de Fourier, l'identité de Parseval et la formule de Plancherel doivent être vérifiées.
On a θ et δ qui appartiennent à S. De là, on peut en déduire que:
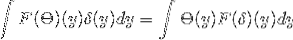
Obtenir
1 / (2π)ré F [θ ], F [δ] L'identité de Parseval
1 / (2π)j / 2 || F [θ ] ||LdeuxRré Formule Plancherel
Transformée de Fourier d'un produit de convolution
Poursuivant des objectifs similaires à ceux de la transformée de Laplace, la convolution des fonctions renvoie au produit entre leurs transformées de Fourier.
Nous avons f et g comme 2 fonctions bornées, définies et complètement intégrables:
F (f * g) = F (f). F (g)
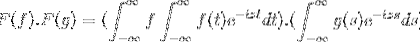
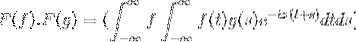
Puis lors du changement de variable
t + s = x; il continue avec la double intégrale incorrecte
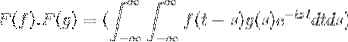
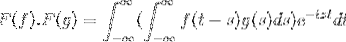
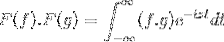
F (f). F (g) = F (f. G)
Continuité et chute à l'infini
Pour tout θ qui appartient à R, F [ θ] obéit aux critères d'une fonction continue bornée dans Rré.
Aussi F [ θ] (y) → 0 dans C si | y | → ∞
Histoire
Ce concept mathématique a été présenté par Joseph B.Fourier en 1811 lors de l'élaboration d'un traité sur la propagation de la chaleur. Il a été rapidement adopté par diverses branches de la science et de l'ingénierie.
Il a été établi comme le principal outil de travail dans l'étude des équations à dérivées partielles, même en le comparant à la relation de travail existante entre les Transformée de Laplace et équations différentielles ordinaires.
À quoi sert la transformée de Fourier?
Il sert principalement à simplifier considérablement les équations, tout en transformant des expressions dérivées en éléments de puissance, dénotant des expressions différentielles sous la forme de polynômes intégrables..
Dans l'optimisation, la modulation et la modélisation des résultats, il agit comme une expression standardisée, étant une ressource fréquente pour l'ingénierie après plusieurs générations.
La série Fourier
Ce sont des séries définies en termes de cosinus et de sinus; Ils servent à faciliter le travail avec les fonctions périodiques générales. Lorsqu'elles sont appliquées, elles font partie des techniques de résolution d'équations différentielles ordinaires et partielles..
Les séries de Fourier sont encore plus générales que les séries de Taylor, car elles développent des fonctions discontinues périodiques qui n'ont pas de représentation en série de Taylor..
Autres formes de la série de Fourier
Pour comprendre analytiquement la transformée de Fourier, il est important de passer en revue les autres façons dont la série de Fourier peut être trouvée, jusqu'à ce que nous puissions définir la série de Fourier dans sa notation complexe.
-Série de Fourier sur une fonction de période 2L
Plusieurs fois, il est nécessaire d'adapter la structure d'une série de Fourier à des fonctions périodiques dont la période est p = 2L> 0 dans l'intervalle [-L, L].
-Série de Fourier dans les fonctions impaires et paires
L'intervalle [-π, π] est considéré, ce qui offre des avantages en tirant parti des caractéristiques symétriques des fonctions.
Si f est pair, la série de Fourier est établie comme une série de cosinus.
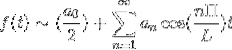
Si f est impair, la série de Fourier est établie comme une série de sinus.
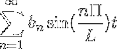
-Notation complexe de la série de Fourier
Si nous avons une fonction f (t), qui répond à toutes les exigences de développabilité de la série de Fourier, il est possible de la désigner dans l'intervalle [-t, t] en utilisant sa notation complexe:
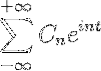
Applications

Calcul de la solution fondamentale
La transformée de Fourier est un outil puissant dans l'étude des équations aux dérivées partielles de type linéaire à coefficients constants. Ils s'appliquent également aux fonctions avec des domaines illimités.
Comme la transformée de Laplace, la transformée de Fourier transforme une fonction dérivée partielle en une équation différentielle ordinaire beaucoup plus simple à opérer..
Le problème de Cauchy pour l'équation de la chaleur présente un domaine d'application fréquente de la transformée de Fourier où la fonction est générée noyau chauffant ou noyau Dirichlet.
Concernant le calcul de la solution fondamentale, les cas suivants sont présentés où il est courant de trouver la transformée de Fourier:
-Équation de Laplace
-Équation de chaleur
-Équation de Schrödinger
-Équation de vague
Théorie du signal
La raison générale de l'application de la transformée de Fourier dans cette branche est principalement due à la décomposition caractéristique d'un signal en superposition infinie de signaux plus facilement traitables.
Il peut s'agir d'une onde sonore ou d'une onde électromagnétique, la transformée de Fourier l'exprime dans une superposition d'ondes simples. Cette représentation est assez fréquente en électrotechnique.
D'autre part, il existe des exemples d'application de la transformée de Fourier dans le domaine de la théorie du signal:
-Problèmes d'identification du système. Établi f et g
-Problème de cohérence du signal de sortie
-Problèmes de filtrage du signal
Exemples
Exemple 1
Définissez la transformée de Fourier pour l'expression suivante:
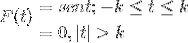
Nous pouvons également le représenter de la manière suivante:
F (t) = Sen (t) [H(t + k) - H(t - k) ]
L'impulsion rectangulaire est définie:
p (t) = H(t + k) - H(t - k)
La transformée de Fourier est appliquée à l'expression suivante qui ressemble au théorème de modulation.
f (t) = p (t) Sen (t)
Où: F [w] = (1/2) i [p (w + 1) - p (w - 1)]
Et la transformée de Fourier est définie par:
F [w] = (1/2) i [(2 / 2w + 1) Sen (k (w + 1)) - (2 / 2w + 1) Sen (k (w-1))]
Exemple 2
Définissez la transformée de Fourier pour l'expression:
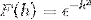
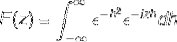
Puisque f (h) est une fonction paire, on peut dire que
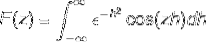
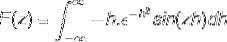
L'intégration par pièces est appliquée en sélectionnant les variables et leurs différentiels comme suit
u = sin (zh) du = z cos (zh) dh
dv = h (e-h)deux v = (e-h)deux / deux
En vous remplaçant, vous avez
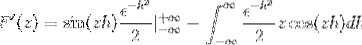
Après évaluation sous le théorème fondamental du calcul
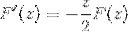
En appliquant les connaissances antérieures concernant les équations différentielles du premier ordre, l'expression est notée
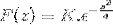
Pour obtenir K on évalue
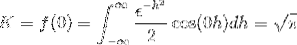
Enfin, la transformée de Fourier de l'expression est définie comme
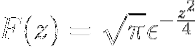
Exercices proposés
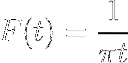
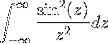
- Obtenez la transformation de l'expression W / (1 + wdeux)
Les références
- Duoandikoetxea Zuazo, J., analyse de Fourier. Addison- Wesley Iberoamericana, Université autonome de Madrid, 1995.
- Lions, J. L., Analyse mathématique et méthodes numériques pour la science et la technologie. Springer-Verlag, 1990.
- Lieb, E. H., les noyaux gaussiens n'ont que des maximiseurs gaussiens. Inventer. Math. 102, 179-208, 1990.
- Dym, H., McKean, H. P., Série Fourier et Intégrales. Presse académique, New York, 1972.
- Schwartz, L., Théorie des Distributions. Ed. Hermann, Paris, 1966.

Personne n'a encore commenté ce post.