
Équation de direction vectorielle de la ligne, exercices résolus
Il est compris par vecteur directeur celui qui définit la direction d'une ligne, soit dans le plan, soit dans l'espace. Par conséquent, un vecteur parallèle à la ligne peut être considéré comme un vecteur directeur de la même.
Ceci est possible grâce à un axiome de la géométrie euclidienne qui dit que deux points définissent une ligne. Puis le segment orienté formé par ces deux points définit également un vecteur directeur de ladite ligne.
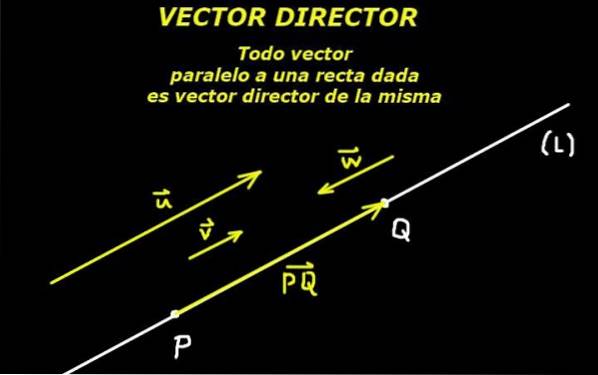
Étant donné un point P appartenant à la lignée (L) et donné un vecteur directeur ou alors de cette ligne, la ligne est complètement déterminée.
Index des articles
- 1 Équation de la ligne et du vecteur directeur
- 1.1 Équation paramétrique de la droite
- 2 La ligne sous forme vectorielle
- 2.1 Exemple 2
- 2.2 Forme continue de la ligne et du vecteur directeur
- 3 Forme générale de l'équation de la droite
- 3.1 Exemple 3
- 4 Forme standard de l'équation de la droite
- 4.1 Exemple 4
- 5 exercices résolus
- 5.1 -Exercice 1
- 5.2 -Exercice 2
- 6 Références
Équation de la ligne et du vecteur directeur
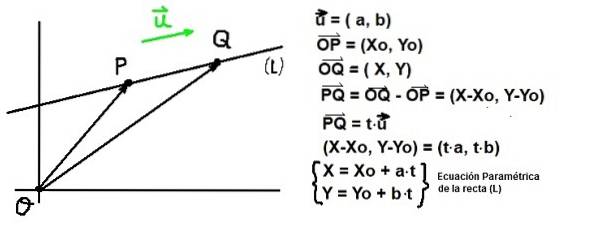
Étant donné un point P de coordonnées Q: (Xo, je) et un vecteur ou alors directeur d'une hétéro (L), tout point Q de coordonnées Q: (X, Y) doit satisfaire que le vecteur PQ être parallèle à u. Cette dernière condition est garantie si PQ est proportionnel à ou alors:
PQ = t⋅ou alors
dans l'expression précédente t est un paramètre qui appartient aux nombres réels.
Si les composantes cartésiennes de PQ et de ou alors L'équation ci-dessus s'écrit comme suit:
(X-Xo, Y-Yo) = t⋅ (a, b)
Si les composantes de l'égalité vectorielle sont égalisées, nous avons la paire d'équations suivante:
X - Xo = a⋅t Oui Y - I = b⋅t
Équation paramétrique de la ligne
Les coordonnées X et Oui d'un point sur la ligne (L) passant par un point de coordonnées (Xo, je) et c'est parallèle à vecteur directeur ou alors= (a, b) sont déterminés en attribuant des valeurs réelles au paramètre variable t:
X = Xo + a⋅t; Y = I + b⋅t
Exemple 1
Pour illustrer la signification de l'équation paramétrique de la droite, nous prenons comme vecteur directeur
ou alors = (a, b) = (2, -1)
et en tant que point connu de la ligne, le point
P = (Xo, I) = (1, 5).
L'équation paramétrique de la droite est:
X = 1 + 2⋅t; Y = 5 - 1⋅t; -∞
Pour illustrer la signification de cette équation, la figure 3 est montrée, où le paramètre t change de valeur et le point Q de coordonnées (X, Y) prendre différentes positions sur la ligne droite.
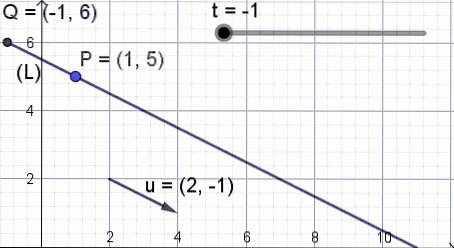
La ligne sous forme vectorielle
Étant donné un point P sur la droite et son vecteur directeur u, l'équation de la droite peut s'écrire sous forme vectorielle:
OQ = OP + λ⋅ou alors
Dans l'équation ci-dessus, Q est n'importe quel point mais appartenant à la droite et λ un nombre réel.
L'équation vectorielle de la ligne est applicable à n'importe quel nombre de dimensions, même une hyper-ligne peut être définie.
Dans le cas tridimensionnel d'un vecteur directeur ou alors= (a, b, c) et un point P = (Xo, Yo, Zo), les coordonnées d'un point générique Q = (X, Y, Z) appartenant à la ligne est:
(X Y Z) = (Xo, Yo, Zo) + λ⋅ (a, b, c)
Exemple 2
Considérons à nouveau la ligne qui a comme vecteur directeur
ou alors = (a, b) = (2, -1)
et en tant que point connu de la ligne, le point
P = (Xo, I) = (1, 5).
L'équation vectorielle de cette ligne est:
(X, Y) = (1, 5) + λ⋅ (2, -1)
Forme continue de la ligne et du vecteur directeur
En partant de la forme paramétrique, en effaçant et en égalisant le paramètre λ, on a:
(X-Xo) / a = (Y-Yo) / b = (Z-Zo) / c
C'est la forme symétrique de l'équation de la droite. Je sens ça à, b Oui c sont les composants du vecteur directeur.
Exemple 3
Considérez la ligne qui a comme vecteur directeur
ou alors = (a, b) = (2, -1)
et en tant que point connu de la ligne, le point
P = (Xo, I) = (1, 5). Trouvez sa forme symétrique.
La forme symétrique ou continue de la ligne est:
(X - 1) / 2 = (Y - 5) / (- 1)
Forme générale de l'équation de la droite
L'équation qui a la structure suivante est connue sous le nom de forme générale de la ligne dans le plan XY:
A⋅X + B⋅Y = C
L'expression de la forme symétrique peut être réécrite pour avoir la forme générale:
b⋅X - a⋅Y = b⋅Xo - a⋅Yo
en comparant avec la forme générale de la ligne, c'est:
A = b, B = -a et C = b⋅Xo - a⋅Yo
Exemple 3
Trouvez la forme générale de la droite dont le vecteur directeur est u = (2, -1)
et qui passe par le point P = (1, 5).
Pour trouver la forme générale, nous pouvons utiliser les formules données, cependant un chemin alternatif sera choisi.
On commence par trouver le vecteur dual w du vecteur directeur u, défini comme le vecteur obtenu en échangeant les composantes de u et en multipliant la seconde par -1:
w= (-1, -2)
le double vecteur w correspond à une rotation de 90 ° dans le sens des aiguilles d'une montre du vecteur directeur v.
Nous nous multiplions de manière scalaire w avec (X, Y) et avec (Xo, je) et nous assortissons:
(-1, -2) • (X, Y) = (-1, -2) • (1, 5)
-X-2Y = -1 -2⋅5 = -11
restant enfin:
X + 2Y = 11
Forme standard de l'équation de la droite
Il s'agit de la forme standard de la ligne dans le plan XY, qui a la structure suivante:
Y = m⋅X + d
où m représente la pente et d l'intersection avec l'axe Y.
Étant donné le vecteur direction u = (a, b), la pente m est b / a.
Y d est obtenu en substituant X et Y au point connu Xo, I:
I = (b / a) Xo + d.
En bref, m = b / a et d = I - (b / a) Xo
Notez que la pente m est le quotient entre la composante Oui du vecteur directeur et du composant X du même.
Exemple 4
Trouvez la forme standard de la ligne dont le vecteur directeur est u = (2, -1)
et qui passe par le point P = (1, 5).
m = -½ et d = 5 - (-½) 1 = 11/2
Y = (-1/2) X + 11/2
Exercices résolus
-Exercice 1
Trouver un vecteur directeur de la droite (L) qui est l'intersection du plan (Π): X - Y + Z = 3 et du plan (Ω): 2X + Y = 1.
Puis écrivez la forme continue de l'équation de la droite (L).
Solution
D'après l'équation du jeu plan (Ω) Y: Y = 1 -2X
Puis on substitue dans l'équation du plan (Π):
X - (1 - 2X) + Z = 3 ⇒ 3X + Z = 4 ⇒ Z = 4 - 3X
Puis on paramétre X, on choisit le paramétrage X = λ
Cela signifie que la ligne a une équation vectorielle donnée par:
(X, Y, Z) = (λ, 1 - 2λ, 4 - 3λ)
qui peut être réécrit comme:
(X, Y, Z) = (0, 1, 4) + λ (1, -2, -3)
avec lequel il est clair que le vecteur ou alors = (1, -2, -3) est un vecteur directeur de la droite (L).
La forme continue de la ligne (L) est:
(X - 0) / 1 = (Y - 1) / (- 2) = (Z - 4) / (- 3)
-Exercice 2
Compte tenu de l'avion 5X + à Y + 4Z = 5
et la droite dont l'équation est X / 1 = (Y-2) / 3 = (Z -2) / (- 2)
Déterminez la valeur de à pour que le plan et la ligne soient parallèles.
Solution 2
Le vecteur n = (5, a, 4) est un vecteur normal au plan.
Le vecteur ou alors = (1, 3, -2) est un vecteur directeur de la ligne.
Si la ligne est parallèle au plan, alors n • v = 0.
(5, à, 4)•(1, 3, -2) = 5 +3à -8 = 0 ⇒ à= 1.
Les références
- Fleming, W. et Varberg, D. E. (1989). Mathématiques Precalculus. Prentice Hall PTR.
- Kolman, B. (2006). Algèbre linéaire. Éducation Pearson.
- Leal, J. M. et Viloria, N. G. (2005). Géométrie analytique plane. Mérida - Venezuela: Editorial Venezolana C. A.
- Navarro, Rocio. Vecteurs. Récupéré de: books.google.co.ve.
- Pérez, C. D. (2006). Précalcul. Éducation Pearson.
- Prenowitz, W. 2012. Concepts de base de la géométrie. Rowman et Littlefield.
- Sullivan, M. (1997). Précalcul. Éducation Pearson.


Personne n'a encore commenté ce post.