
Vitesse aréolaire comment elle est calculée et les exercices sont résolus
La vitesse aréolaire est la zone balayée par unité de temps et est constante. Elle est spécifique à chaque planète et découle de la description de la deuxième loi de Kepler sous forme mathématique. Dans cet article, nous expliquerons ce que c'est et comment il est calculé.
Le boom qui représente la découverte de planètes en dehors du système solaire a ravivé l'intérêt pour le mouvement planétaire. Rien ne suggère que ces exo-planètes suivent des lois autres que celles déjà connues et valables dans le système solaire: les lois de Kepler..
Johannes Kepler était l'astronome qui, sans l'aide du télescope et en utilisant les observations de son mentor Tycho Brahe, a créé un modèle mathématique qui décrit le mouvement des planètes autour du Soleil..
Il a laissé ce modèle incarné dans les trois lois qui portent son nom et qui restent aussi valables aujourd'hui qu'en 1609, lorsqu'il a établi les deux premières et en 1618, date à laquelle il a énoncé la troisième..
Index des articles
- 1 Lois de Kepler
- 2 Pourquoi les planètes se déplacent-elles de manière elliptique autour du Soleil?
- 3 L'amplitude de la vitesse linéaire d'une planète n'est pas constante
- 4 Vitesse aréolaire
- 5 Calcul de la vitesse linéaire et de la vitesse aréolaire
- 5.1 Exercice
- 6 Bibliographie
Lois de Kepler
Dans le langage d'aujourd'hui, les trois lois de Kepler se lisent comme suit:
1. Les orbites de toutes les planètes sont elliptiques et le Soleil est focalisé.
2. Le vecteur de position du Soleil à une planète balaie des zones égales en des temps égaux.
3. Le carré de la période orbitale d'une planète est proportionnel au cube du demi-grand axe de l'ellipse décrite..
Une planète aura une vitesse linéaire, comme tout objet en mouvement connu. Et il y a encore plus: lors de l'écriture de la deuxième loi de Kepler sous forme mathématique, un nouveau concept apparaît appelé vitesse aréolaire, typique de chaque planète..
Pourquoi les planètes se déplacent-elles de manière elliptique autour du Soleil?
La Terre et les autres planètes se déplacent autour du Soleil grâce au fait qu'elle exerce une force sur elles: l'attraction gravitationnelle. La même chose se produit avec toute autre étoile et les planètes qui composent son système, si elle en a..
Il s'agit d'une force du type connu sous le nom de force centrale. Le poids est une force centrale que tout le monde connaît. L'objet qui exerce la force centrale, que ce soit le Soleil ou une étoile lointaine, attire les planètes vers son centre et elles se déplacent dans une courbe fermée.
En principe, cette courbe peut être approximée comme une circonférence, comme l'a fait Nicolás Copernic, un astronome polonais qui a créé la théorie héliocentrique..
La force responsable est l'attraction gravitationnelle. Cette force dépend directement des masses de l'étoile et de la planète en question et est inversement proportionnelle au carré de la distance qui les sépare..
Le problème n'est pas si simple, car dans un système solaire, tous les éléments interagissent de cette manière, ajoutant de la complexité à la matière. De plus, ce ne sont pas des particules, car les étoiles et les planètes ont une taille mesurable..
Pour cette raison, le point central de l'orbite ou du circuit parcouru par les planètes n'est pas exactement centré sur l'étoile, mais en un point connu comme le centre de gravité du système Soleil-planète..
L'orbite résultante est elliptique. L'image suivante le montre, en prenant la Terre et le Soleil comme exemple:
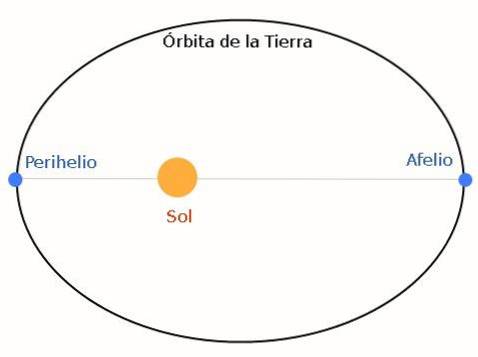
L'aphélie est la position la plus éloignée sur Terre du Soleil, tandis que le périhélie est le point le plus proche. L'ellipse peut être plus ou moins aplatie, selon les caractéristiques du système étoile-planète..
Les valeurs de l'aphélie et du périhélie varient chaque année, car les autres planètes provoquent des perturbations. Pour les autres planètes, ces positions sont appelées respectivement apoaster et périaster..
L'amplitude de la vitesse linéaire d'une planète n'est pas constante
Kepler a découvert que lorsqu'une planète tourne autour du Soleil, pendant son mouvement, elle balaie des zones égales en des temps égaux. La figure 2 montre graphiquement la signification de ceci:
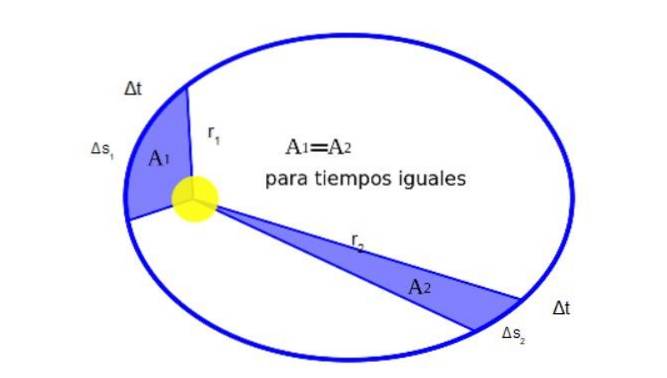
Mathématiquement, le fait que A1 être égal à Adeux s'exprime comme ceci:

Les arcs parcourus Δs sont petits, de sorte que chaque aire peut se rapprocher de celle d'un triangle:
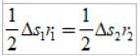
Puisque Δs =vΔt, où v est la vitesse linéaire de la planète en un point donné, en substituant on a:
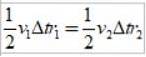
Et comme l'intervalle de temps Δt est le même, on obtient:
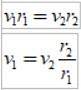
Comme rdeux > r1, puis v1 > vdeux, en d'autres termes, la vitesse linéaire d'une planète n'est pas constante. En fait, la Terre va plus vite lorsqu'elle est en périhélie que lorsqu'elle est en aphélie..
Par conséquent, la vitesse linéaire de la Terre ou de toute planète autour du Soleil n'est pas une grandeur qui sert à caractériser le mouvement de ladite planète..
Vitesse aréolaire
La deuxième loi de Kepler suggère une nouvelle grandeur appelée vitesse aréolaire. Elle est définie comme la zone balayée par unité de temps et est constante. Pour le calculer, le chiffre suivant est utilisé:
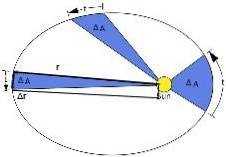
Une petite zone balayée par la Terre est choisie en faisant son circuit elliptique, que nous désignerons par ΔA. Le temps nécessaire pour cela est Δt.
La figure 3 montre le vecteur de position de la Terre par rapport au Soleil, noté r. Lorsque la Terre bouge, elle subit un déplacement Δr.
Cette zone correspond à la moitié de la zone du rectangle représenté sur la figure 3:
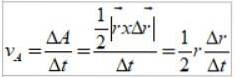
Le quotient Δr / Δt est précisément la vitesse linéaire de la Terre, donc la vitesse aréolaire est la suivante:
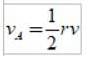
Les unités de vÀ dans le système international, ils sont:
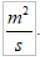
Notez que bien que r et v varient, le produit reste constant. Cela fait de la vitesse aréolaire une magnitude très adéquate pour caractériser le mouvement d'une planète autour de son étoile..
Le produit de r et v est la grandeur du moment cinétique L, de sorte que la vitesse aréolaire peut être exprimée comme:
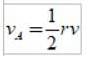
Calcul de la vitesse linéaire et de la vitesse aréolaire
Avec l'exemple suivant, nous montrerons comment calculer la vitesse aréolaire lorsque certains paramètres du mouvement planétaire sont connus:
Exercer
Une exo-planète se déplace autour de son soleil en suivant une orbite elliptique, selon les lois de Kepler. Lorsqu'il est dans le périaster, son rayon vecteur est r1 = 4 107 km, et quand il est en apoastro c'est rdeux = 15 107 km. La vitesse linéaire à son périaster est v1 = 1000 km / s.
Calculer:
A) L'amplitude de la vitesse à l'apoastro.
B) La vitesse aréolaire de l'exo-planète.
C) La longueur du demi-grand axe de l'ellipse.
Réponds à)
L'équation est utilisée:
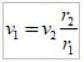
dans lequel les valeurs numériques sont substituées.
Chaque terme est identifié comme suit:
v1 = vitesse en apoastro; vdeux = vitesse dans le périastre; r1= distance d'apoastro,
rdeux= distance du périastre.
Avec ces valeurs, vous obtenez:

Réponse B)
L'équation à utiliser est
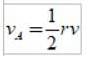
dans laquelle la paire de valeurs r et v du périaster ou de l'apoaster peut être substituée, puisque vÀ est une constante de la planète:

Réponse C)
La longueur du demi-grand axe de l'ellipse est le demi-total de l'apoaster et du périaster:
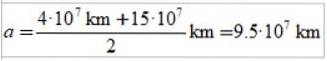
Bibliographie
- Serway, R., Jewett, J. (2008). Physique pour la science et l'ingénierie. Volume 1. Mexique. Éditeurs d'apprentissage Cengage. 367-372.
- Stern, D. (2005). Les trois lois du mouvement planétaire de Kepler. Récupéré de pwg.gsfc.nasa.gov
- Remarque: l'exercice proposé a été repris et modifié à partir du texte suivant dans un livre McGrawHill. Malheureusement, il s'agit d'un chapitre isolé au format pdf, sans le titre ni l'auteur: mheducation.es/bcv/guide/capitulo/844817027X.pdf

Personne n'a encore commenté ce post.