
Concepts, méthodes, exemples d'analyse de maillage
le analyse de maillage est une technique utilisée pour résoudre les circuits électriques plats. Cette procédure peut également apparaître dans la littérature sous les noms de méthode du courants de circuit ou méthode de courants de maillage (ou boucle).
Le fondement de cette méthode et d'autres méthodes d'analyse des circuits électriques est dans les lois de Kirchhoff et la loi d'Ohm. Les lois de Kirchhoff, quant à elles, sont l'expression de deux principes très importants de conservation en physique pour les systèmes isolés: la charge électrique et l'énergie sont conservées..

D'une part, la charge électrique est liée au courant, qui est la charge en mouvement, tandis que dans un circuit, l'énergie est liée à la tension, qui est l'agent chargé de faire le travail nécessaire pour maintenir la charge en mouvement..
Ces lois, appliquées à un circuit plat, génèrent un ensemble d'équations simultanées qu'il faut résoudre pour obtenir les valeurs de courant ou de tension..
Le système d'équations peut être résolu avec des techniques analytiques familières, telles que règle du crameur, qui nécessite le calcul des déterminants pour obtenir la solution du système.
En fonction du nombre d'équations, elles sont résolues à l'aide d'une calculatrice scientifique ou d'un logiciel mathématique. Sur le net, de nombreuses options sont également disponibles.
Index des articles
- 1 Termes importants
- 2 méthodes
- 2.1 - Etapes pour appliquer l'analyse de maillage
- 3 exercices résolus
- 3.1 - Exemple 1
- 3.2 - Exemple 2
- 4 Références
Termes importants
Avant d'expliquer son fonctionnement, nous commencerons par définir ces termes:
Branche: section contenant un élément de circuit.
Nœud: point reliant deux ou plusieurs branches.
Lien: est une partie fermée d'un circuit, commençant et se terminant au même nœud.
Engrener: boucle qui ne contient aucune autre boucle à l'intérieur (maille essentielle).
Méthodes
L'analyse de maillage est une méthode générale utilisée pour résoudre des circuits dont les éléments sont connectés en série, en parallèle ou de manière mixte, c'est-à-dire lorsque le type de connexion n'est pas clairement distingué. Le circuit doit être plat, ou du moins il doit être possible de le redessiner comme tel.
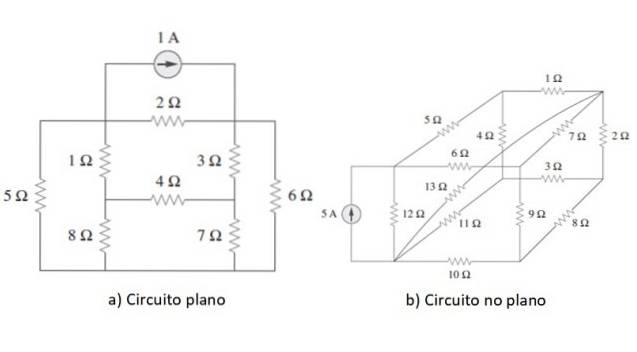
Un exemple de chaque type de circuit est illustré dans la figure ci-dessus. Une fois le point clarifié, pour commencer, nous appliquerons la méthode à un circuit simple à titre d'exemple dans la section suivante, mais d'abord nous passerons brièvement en revue les lois d'Ohm et Kirchhoff..
Loi d'Ohm: être V la tension, R résistance e je le courant de l'élément résistif ohmique, dans lequel la tension et le courant sont directement proportionnels, la résistance étant la constante de proportionnalité:
V = I.R
Loi de la tension de Kirchhoff (LKV): Dans tout chemin fermé parcouru dans une seule direction, la somme algébrique des tensions est nulle. Cela inclut les tensions dues aux sources, résistances, inductances ou condensateurs: ∑ E = ∑ Rje. je
Loi du courant de Kirchhoff (LKC): à n'importe quel nœud, la somme algébrique des courants est nulle, en tenant compte du fait que les courants entrants se voient attribuer un signe et ceux qui en quittent un autre. De cette façon: ∑ I = 0.
Avec la méthode du courant de maillage, il n'est pas nécessaire d'appliquer la loi actuelle de Kirchhoff, ce qui entraîne moins d'équations à résoudre.
- Étapes d'application de l'analyse de maillage
Nous commencerons par expliquer la méthode pour un circuit à 2 mailles. La procédure peut alors être étendue pour les circuits plus grands.
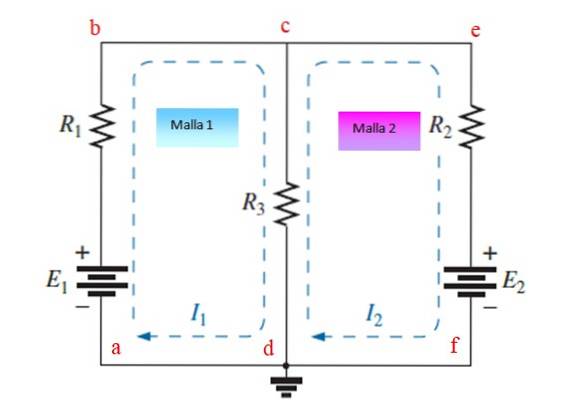
Étape 1
Attribuez et dessinez des courants indépendants à chaque maillage, dans cet exemple, ils sont je1 et jedeux. Ils peuvent être dessinés dans le sens horaire ou antihoraire.
Étape 2
Appliquez la loi des tensions de Kirchhoff (LTK) et la loi d'Ohm à chaque maillage. Les chutes potentielles reçoivent un signe (-) tandis que les hausses se voient attribuer un signe (+).
Maille abcda
En partant du point a et en suivant le sens du courant, on trouve une élévation de potentiel de la batterie E1 (+), puis une baisse de R1 (-) puis une autre baisse de R3 (-).
Simultanément, la résistance R3 est également traversé par le courant Ideux, mais dans la direction opposée, cela représente donc une hausse (+). La première équation ressemble à ceci:
ET1-R1.je1 -R3.je1 + R3.jedeux = 0
Ensuite, il est factorisé et les termes sont regroupés:
- (R1+R3) JE1 +R3jedeux = -E1 (Équation 1)
Maillage Cefdc
Partir du point et et suivant la direction du courant, une baisse de potentiel se trouve dans Rdeux (-), encore une fois ETdeux, puisque le courant entre par le pôle + de la batterie et enfin une autre baisse R3 (-), en même temps le courant je1 traverse R3 dans le sens opposé (+).
La deuxième équation, avec les signes indiqués, ressemble à ceci:
- Rdeux jedeux - ETdeux -R3 jedeux +R3 je1= 0
R3je1 - (Rdeux +R3) jedeux = Edeux (Équation 2)
Notez qu'il existe deux équations avec les deux inconnues I1 et moideux.
Étape 3
Le système d'équations ainsi formé est alors résolu.
Exercices résolus
Pour commencer, il est important de prendre en compte les éléments suivants:
-Les courants de boucle ou les courants de maillage peuvent se voir attribuer une adresse arbitraire.
-Chaque maillage essentiel - ou «fenêtre» - que possède le circuit doit se voir attribuer un courant.
-Les courants de maillage sont indiqués par une lettre majuscule pour les distinguer des courants qui circulent à travers les branches, bien que dans certains cas le courant qui circule à travers une branche puisse être le même que celui du maillage.
- Exemple 1
Trouvez les courants qui traversent chaque résistance dans le circuit de la figure 3, si les éléments ont les valeurs suivantes:
R1 = 20 Ω; Rdeux = 30 Ω; R3 = 10 Ω; ET1 = 12 V; ETdeux = 18 V
Solution
Tout d'abord, il faut attribuer les courants de maillage I1 et moideux et prenez le système d'équations comme déduit dans la section précédente, puis remplacez les valeurs données dans l'instruction:
- (R1+R3) JE1 +R3jedeux = -E1 (Équation 1)
R3je1 - (Rdeux +R3) jedeux = Edeux (Équation 2)
-
-(20 + 30) je1 + 10Ideux = -12
10I1 - (30 +10) JEdeux = 18
--
-cinquanteje1 + 10Ideux = -12
10I1 - 40 JEdeux = 18
Puisqu'il s'agit d'un système d'équations 2 x 2, il peut être facilement résolu par réduction, en multipliant la deuxième équation par 5 pour éliminer l'inconnu je1:
-cinquanteje1 + 10 JEdeux = -12
50I1 - 200 Ideux = 90
-
-190 Ideux= 78
jedeux = - 78/180 A = - 0,41 A
Immédiatement le courant disparaît je1 à partir de l'une des équations d'origine:
je1 = (18 + 40 Ideux) / 10 = (18 + 40 x (-0,41)) / 10 = 0,16 A
Le signe négatif dans le courant jedeux signifie que le courant dans la maille 2 circule dans le sens opposé à celui tiré.
Les courants dans chaque résistance sont les suivants:
Pour la résistance R1 le courant circule je1 = 0,16 A dans le sens dessiné, par résistance Rdeux le courant circule jedeux = 0,41 A dans la direction opposée à celle dessinée, et par la résistance R3 circuler je3 = 0,16- (-0,41) A = 0,57 A vers le bas.
Solution système par la méthode de Cramer
Sous forme matricielle, le système peut être résolu comme suit:
Étape 1: Calculez Δ

Étape 2: Calculez Δ1
La première colonne est remplacée par les termes indépendants du système d'équations, en conservant l'ordre dans lequel le système a été initialement proposé:

Étape 3: Calculez I1
je1 = Δ1/ Δ = 300/1900 = 0,16 A
Étape 4: Calculez Δdeux

jedeux = Δdeux/ Δ = -780/1900 = -0,41 Un
- Exemple 2
Déterminez le courant et les tensions à travers chaque résistance dans le circuit suivant, en utilisant la méthode des courants de maillage:

Solution
Les trois courants de maillage sont tracés, comme le montre la figure suivante, dans des directions arbitraires. Maintenant, les maillages sont parcourus à partir de n'importe quel point:
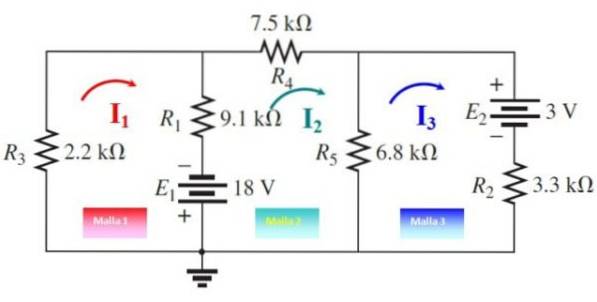
Maille 1
-9100.I1+18-2200.I1+9100.Ideux= 0
-11300 I1 + 9100.Ideux = -18
Maille 2
-(7500 + 6800 + 9100) .Ideux + 9100.I1+6800.I3-18 = 0
9100.I1 - 23400.Ideux + 6800.I3 = 18
Maille 3
-(6800 + 3300) I3 + 6800.Ideux - 3 = 0
6800.Ideux - 10100.I3 = 3
Système d'équations
-11300 I1 + 9100.Ideux + 0.I3= -18
9100.I1 - 23400.Ideux + 6800.I3 = 18
0.I1 + 6800.Ideux - 10100.I3 = 3
Bien que les nombres soient importants, ils peuvent être résolus rapidement à l'aide d'une calculatrice scientifique. Rappelez-vous que les équations doivent être ordonnées et ajoutez des zéros aux endroits où l'inconnu n'apparaît pas, comme il apparaît ici.
Les courants de maillage sont:
je1 = 0,0012 A; jedeux = -0,00048 A; je3 = -0,00062 Un
Courants jedeux et je3 circulent dans le sens opposé à celui indiqué sur la figure, car ils se sont avérés négatifs.
Tableau des courants et tensions dans chaque résistance
| Résistance (Ω) | Courant (ampères) | Tension = I.R (Volts) |
|---|---|---|
| 9100 | je1 -jedeux = 0,0012 - (- 0,00048) = 0,00168 | 15,3 |
| 3300 | 0,00062 | 2,05 |
| 2200 | 0,0012 | 2,64 |
| 7500 | 0,00048 | 3,60 |
| 6800 | jedeux -je3= -0,00048 - (- 0,00062) = 0,00014 | 0,95 |
Solution de règle de Cramer
Puisqu'il s'agit de grands nombres, il est pratique d'utiliser la notation scientifique pour travailler directement avec eux.
Calcul de I1
Les flèches colorées dans le déterminant 3 x 3 indiquent comment trouver les valeurs numériques en multipliant les valeurs indiquées. Commençons par obtenir ceux de la première tranche dans le déterminant Δ:
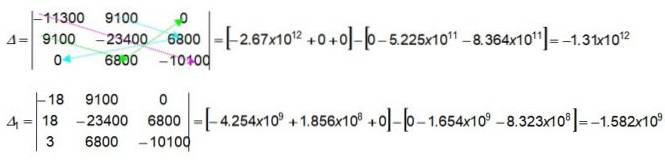
(-11300) x (-23400) x (-10100) = -2,67 x 1012
9100 x 0 x 0 = 0
9100 x 6800 x 0 = 0
Immédiatement, nous obtenons la deuxième parenthèse dans ce même déterminant, qui est travaillée de gauche à droite (pour cette parenthèse, les flèches de couleur n'ont pas été dessinées sur la figure). Nous invitons le lecteur à le vérifier:
0 x (-23400) x 0 = 0
9100 x 9100 x (-10100) = -8,364 x 10Onze
6800 x 6800 x (-11300) = -5,225 x 10Onze
De même, le lecteur peut également vérifier les valeurs du déterminant Δ1.
Important: entre les deux parenthèses il y a toujours un signe négatif.
Enfin, vous obtenez le courant je1 à travers je1 = Δ1 / Δ
je1 = -1,582 x 109/ 1,31 x 1012 = 0,0012 A
Calcul de Ideux
La procédure peut être répétée pour calculer jedeux, dans ce cas, pour calculer le déterminant Δdeux la deuxième colonne du déterminant Δ est remplacée par la colonne des termes indépendants et sa valeur est trouvée, selon la procédure expliquée.
Cependant, comme il est encombrant en raison des grands nombres, surtout si vous n'avez pas de calculatrice scientifique, le plus simple est de remplacer la valeur de je1 déjà calculé, dans l'équation suivante et claire:
-11300 I1 + 9100.Ideux + 0.I3= -18 → 9100 Ideux= -18 + 11300 I1 → jedeux = -0,00048 Un
Calcul de I3
Une fois avec les valeurs de je1 et jedeux en main, celui de je3 trouvé directement par substitution.
Les références
- Alexander, C. 2006. Principes de base des circuits électriques. 3e. Édition. Mc Graw Hill.
- Boylestad, R. 2011. Introduction à l'analyse de circuits.2da. Édition. Pearson.
- Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 5. Interaction électrique. Edité par Douglas Figueroa (USB).
- García, L. 2014. Electromagnétisme. 2ème. Édition. Université industrielle de Santander.
- Sears, Zemansky. 2016. Physique universitaire et physique moderne. 14e. Éd. Volume 2.
Personne n'a encore commenté ce post.