
Charge axiale comment elle est calculée et les exercices résolus
La charge axiale C'est la force qui est dirigée parallèlement à l'axe de symétrie d'un élément qui compose une structure. La force axiale ou la charge peut être une tension ou une compression. Si la ligne d'action de la force axiale coïncide avec l'axe de symétrie qui passe par le centroïde de l'élément considéré, alors on dit qu'il s'agit d'une charge ou force axiale concentrique.
Au contraire, s'il s'agit d'une force axiale ou d'une charge parallèle à l'axe de symétrie, mais dont la ligne d'action n'est pas sur l'axe lui-même, c'est une force axiale excentrique.
-
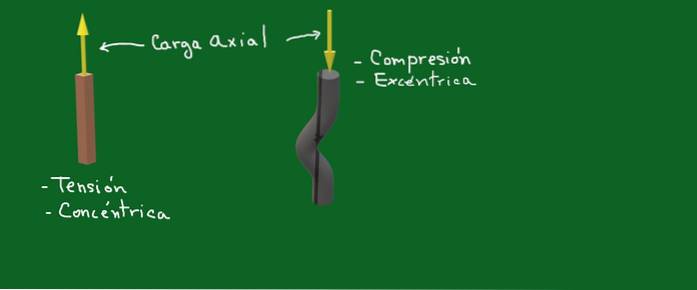
Figure 1. Charge axiale. Source: fait soi-même
Sur la figure 1, les flèches jaunes représentent les forces ou charges axiales. Dans un cas, il s'agit d'une force de tension concentrique et dans l'autre, il s'agit d'une force de compression excentrique.
L'unité de mesure de la charge axiale dans le système international SI est le Newton (N). Mais d'autres unités de force telles que le kilogramme-force (kg-f) et la livre-force (lb-f) sont également fréquemment utilisées..
Index des articles
- 1 Comment est-il calculé?
- 1.1 Relation de la charge axiale avec la contrainte normale
- 2 exercices résolus
- 2.1 -Exercice 1
- 2.2 -Exercice 2
- 3 Références
Comment est-il calculé?
Pour calculer la valeur de la charge axiale dans les éléments d'une structure, les étapes suivantes doivent être suivies:
- Faire le diagramme de force sur chaque élément.
- Appliquer les équations qui garantissent l'équilibre translationnel, c'est-à-dire que la somme de toutes les forces est nulle.
- Considérons l'équation des couples ou des moments pour que l'équilibre rotationnel soit satisfait. Dans ce cas, la somme de tous les couples doit être nulle.
- Calculez les forces et identifiez les forces ou les charges axiales dans chacun des éléments.
Rapport de la charge axiale à la contrainte normale
La contrainte normale moyenne est définie comme le rapport de la charge axiale divisée par la section transversale. Les unités d'effort normal dans le système international S.I. ils sont Newton sur mètre carré (N / m²) ou Pascal (Pa). La figure 2 suivante illustre le concept de contrainte normale pour plus de clarté..
-
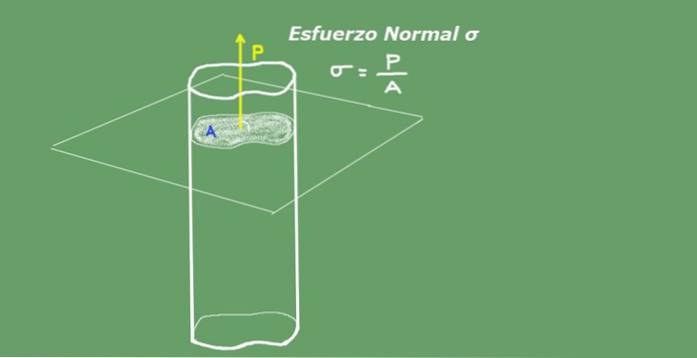
Figure 2. Contrainte normale. Source: fait soi-même.
Exercices résolus
-Exercice 1
Considérons un poteau cylindrique en béton de hauteur h et de rayon r. Supposons que la densité du béton soit ρ. La colonne ne supporte aucune charge supplémentaire autre que son propre poids et est supportée sur une base rectangulaire.
- Trouvez la valeur de la charge axiale aux points A, B, C et D, qui sont dans les positions suivantes: A à la base du poteau, B a ⅓ de hauteur h, C a ⅔ de hauteur h et par le dernier D à le haut de la colonne.
- Déterminez également la contrainte normale moyenne à chacune de ces positions. Prenez les valeurs numériques suivantes: h = 3m, r = 20cm et ρ = 2250 kg / m³
-
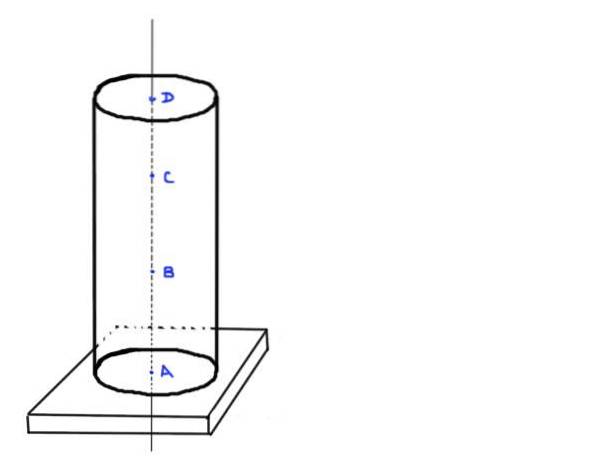
Figure 3. Colonne cylindrique. Source: fait soi-même.
Solution
Poids total de la colonne
Le poids total W de la colonne est le produit de sa densité par le volume multiplié par l'accélération de la pesanteur:
W = ρ ∙ h ∙ π ∙ r² ∙ g = 8313 N
Charge axiale en A
Au point A, la colonne doit supporter tout son poids, de sorte que la charge axiale à ce point est la compression égale au poids de la colonne:
PA = W = 8313 N
Charge axiale en B
Seul ⅔ de la colonne sera sur le point B, donc la charge axiale à ce point sera la compression et sa valeur ⅔ le poids de la colonne:
PB = ⅔ W = 5542 N
Figure 3. Colonne cylindrique. Source: fait soi-même.
Au-dessus de la position C, il n'y a que ⅓ de colonne, donc sa charge axiale de compression sera ⅓ de son propre poids:
PC = ⅓ W = 2771 N
Charge axiale en D
Enfin, il n'y a pas de charge sur le point D, qui est l'extrémité supérieure de la colonne, donc la force axiale en ce point est nulle..
PD = 0 N
Efforts normaux dans chacune des positions
Pour déterminer la contrainte normale dans chacune des positions, il sera nécessaire de calculer la section transversale de l'aire A, qui est donnée par:
A = π ∙ r² = 0,126 m²
De cette manière, la contrainte normale dans chacune des positions sera le quotient entre la force axiale en chacun des points divisée par l'aire de la section transversale déjà calculée, qui dans cet exercice est la même pour tous les points car il s'agit d'un colonne cylindrique.
σ = P / A; σA = 66,15 kPa; σB = 44,10 kPa; σC = 22,05 kPa; σD = 0,00 kPa
-Exercice 2
La figure montre une structure composée de deux barres que nous appellerons AB et CB. La barre AB est supportée à l'extrémité A par une broche et à l'autre extrémité reliée à l'autre barre par une autre broche B.
De même, la barre CB est supportée à l'extrémité C au moyen d'une broche et à l'extrémité B avec la broche B qui la relie à l'autre barre. Une force verticale ou une charge F est appliquée à la broche B comme indiqué dans la figure suivante:
-
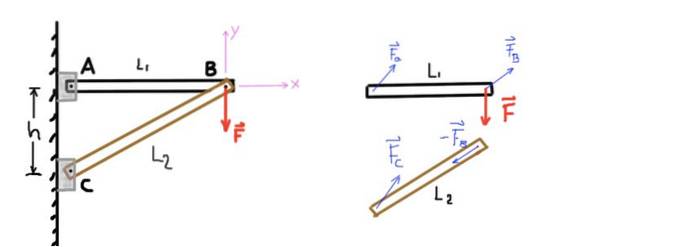
Figure 4. Structure à deux barres et diagramme du corps libre. Source: fait soi-même.
Supposons que le poids des barres soit négligeable, car la force F = 500 kg-f est bien supérieure au poids de la structure. La séparation entre les supports A et C est h = 1,5 m et la longueur de la barre AB est L1 = 2 m. Déterminer la charge axiale sur chacune des barres, en indiquant s'il s'agit d'une charge axiale de compression ou de traction.
Solution 2
La figure montre, au moyen d'un diagramme de corps libre, les forces agissant sur chacun des éléments de la structure. Le système de coordonnées cartésiennes avec lequel les équations d'équilibre des forces seront établies est également indiqué..
Les couples ou moments seront calculés au point B et seront considérés comme positifs s'ils pointent loin de l'écran (axe Z). L'équilibre des forces et des couples pour chaque barre est:
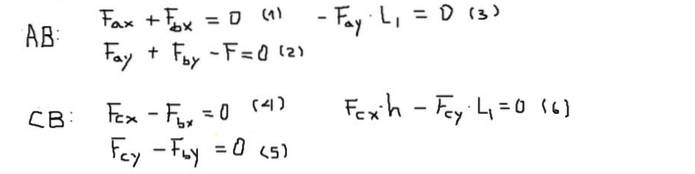
Ensuite, les composantes des forces de chacune des équations sont résolues dans l'ordre suivant:
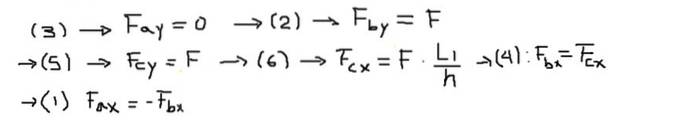
Enfin, les efforts résultants aux extrémités de chaque barre sont calculés:
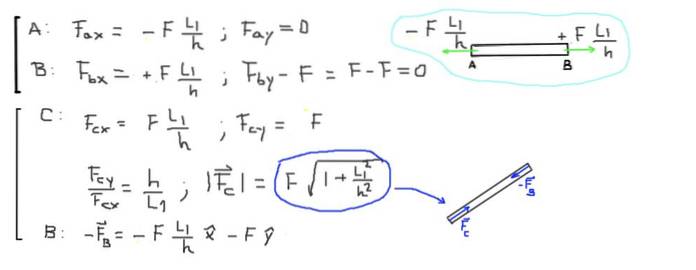
F ∙ (L1 / h) = 500 kg-f ∙ (2,0 m / 1,5 m) = 666,6 kg-f = 6533,3 N
La barre CB est en compression du fait des deux forces agissant à ses extrémités parallèles à la barre et pointant vers son centre. L'amplitude de la force de compression axiale dans la barre CB est:
F ∙ (1 + L1² / h²) 1/2 = 500 kg-f ∙ (1 + (2 / 1,5) ²) 1/2 = 833,3 kg-f = 8166,6 N
Les références
- Beer F… Mécanique des matériaux. 5ème. Édition. 2010. Mc Graw Hill. 1-130.
- Hibbeler R. Mécanique des matériaux. Huitième édition. Prentice Hall. 2011. 3-60.
- Gere J. Mécanique des matériaux. Huitième édition. Apprentissage Cengage. 4-220.
- Giancoli, D. 2006. Physique: principes avec applications. 6e éd. Prentice Hall. 238-242.
- Valera Negrete, J. 2005. Notes sur la physique générale. UNAM. 87-98.
Personne n'a encore commenté ce post.