
Congruence chiffres congruents, critères, exemples, exercices
La congruence, En géométrie, il fait remarquer que si deux figures planes ont la même forme et les mêmes dimensions, elles sont congruentes. Par exemple, deux segments sont congruents lorsque leurs longueurs sont égales. De même, les angles congruents ont la même mesure, même s'ils ne sont pas orientés de la même manière dans le plan..
Le terme «congruence» vient du latin conforme, dont le sens est la correspondance. Ainsi, deux figures congruentes correspondent exactement l'une à l'autre..
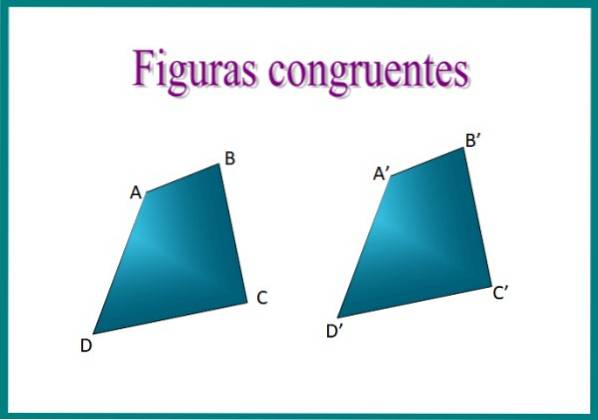
Par exemple, si nous superposons les deux quadrilatères dans l'image, nous constaterons qu'ils sont congruents, puisque la disposition de leurs côtés est identique et qu'ils mesurent la même.
En plaçant les quadrilatères ABCD et A'B'C'D 'l'un sur l'autre, les chiffres correspondront exactement. Les côtés correspondants sont appelés côtés homologues ou alors correspondant et pour exprimer la congruence, le symbole ≡ est utilisé. Alors on peut dire que ABCD ≡ A'B'C'D '.
Index des articles
- 1 Critères de congruence
- 1.1 Congruence, identité et similitude
- 2 Exemples de congruence
- 2.1 - Conguence angulaire
- 2.2 - Congruence des triangles
- 3 exercices résolus
- 3.1 - Exercice 1
- 3.2 - Exercice 2
- 4 Références
Critères de congruence
Les caractéristiques suivantes sont communes aux polygones congruents:
-Même forme et taille.
-Mesures identiques de leurs angles.
-La même mesure sur chacun de ses côtés.
Dans le cas où deux polygones en question sont réguliers, c'est-à-dire que tous les côtés et angles internes mesurent la même, la congruence est assurée lorsqu'elle est remplie quelque des conditions suivantes:
-Les côtés sont congruents
-le apothèmes ils ont la même mesure
-le radio de chaque polygone mesure égal
L'apothème d'un polygone régulier est la distance entre le centre et l'un des côtés, tandis que le rayon correspond à la distance entre le centre et un sommet ou un coin de la figure.
Les critères de congruence sont fréquemment utilisés car de nombreuses pièces et pièces de toutes sortes sont produites en série et doivent avoir la même forme et les mêmes dimensions. De cette manière, ils peuvent être facilement remplacés si nécessaire, par exemple des écrous, des boulons, des feuilles ou des pavés au sol dans la rue..

Congruence, identité et similitude
Il existe des concepts géométriques liés à la congruence, par exemple figures identiques et les chiffres similaires, cela n'implique pas nécessairement que les chiffres sont congruents.
Notez que les figures congruentes sont identiques, cependant les quadrilatères de la figure 1 pourraient être orientés de différentes manières sur le plan et rester toujours congruents, car l'orientation différente ne change pas la taille de leurs côtés ou de leurs angles. Dans ce cas, ils cesseraient d'être identiques.
L'autre concept est celui de la similitude des figures: deux figures planes sont similaires si elles ont la même forme et leurs angles internes mesurent les mêmes, bien que la taille des figures puisse être différente. Si tel est le cas, les chiffres ne sont pas congruents.
Exemples de congruence
- Conguence d'angle
Comme nous l'avons indiqué au début, les angles congruents ont la même mesure. Il existe plusieurs façons d'obtenir des angles congruents:
Exemple 1
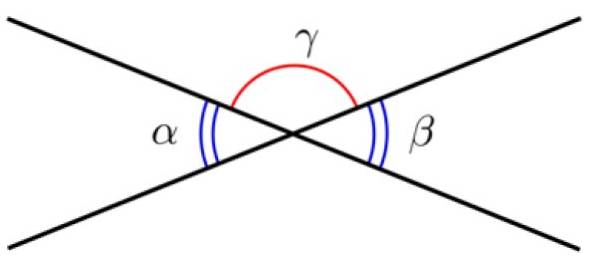
Deux lignes avec un point commun définissent deux angles, appelés Angles opposés par le sommet. Ces angles ont la même mesure, donc ils sont congruents.
Exemple 2
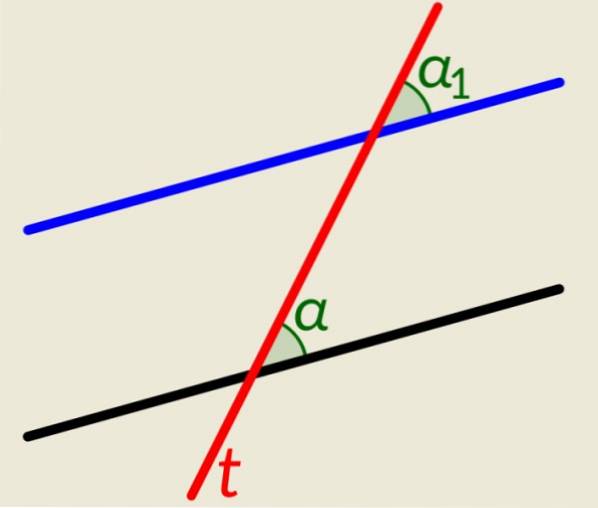
Il y a deux lignes parallèles plus une ligne t qui les croise tous les deux. Comme dans l'exemple précédent, lorsque cette ligne coupe les parallèles, elle génère des angles congruents, un sur chaque ligne du côté droit et deux autres du côté gauche. La figure montre α et α1, à droite de la ligne t, qui sont congruents.
Exemple 3
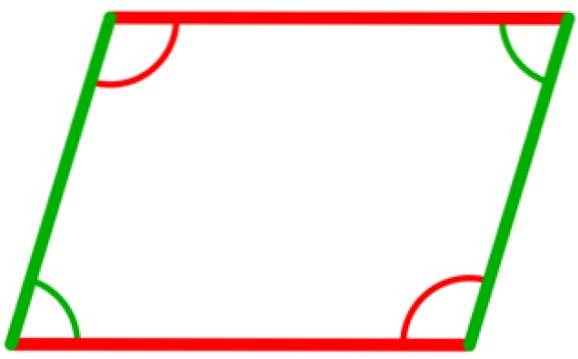
Dans un parallélogramme, il y a quatre angles intérieurs, qui sont congruents de deux à deux. Ce sont ceux qui sont entre les sommets opposés, comme le montre la figure suivante, dans laquelle les deux angles en vert sont congruents, ainsi que les deux angles en rouge.
- Congruence des triangles
Deux triangles de même forme et de même taille sont congruents. Pour vérifier cela, trois critères peuvent être examinés à la recherche de congruence:
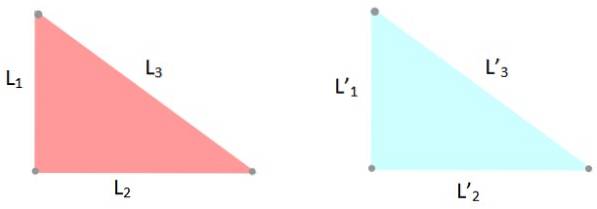
-Critère LLL: les trois côtés des triangles ont les mêmes mesures, donc L1 = L '1; Ldeux = L 'deux et moi3 = L '3.
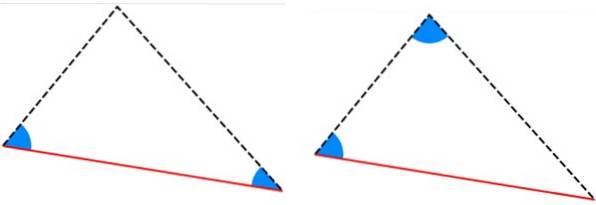
-Critères ALA et AAL: les triangles ont deux angles intérieurs égaux et le côté entre ces angles a la même mesure.
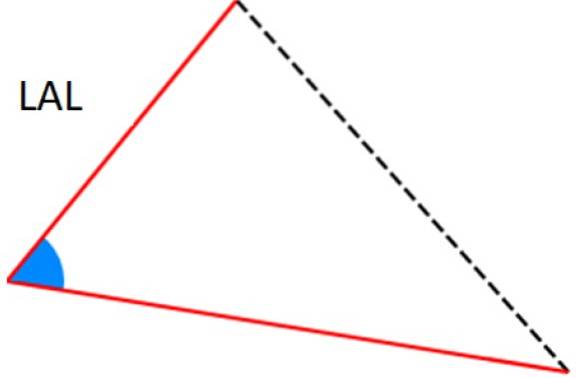
-Critère LAL: deux des côtés sont identiques (correspondants) et entre eux il y a le même angle.
Exercices résolus
- Exercice 1
Deux triangles sont représentés sur la figure suivante: ΔABC et ΔECF. On sait que AC = EF, que AB = 6 et que CF = 10. De plus, les angles ∡BAC et ∡FEC sont congruents et les angles ∡ACB et ∡FCB sont également congruents..
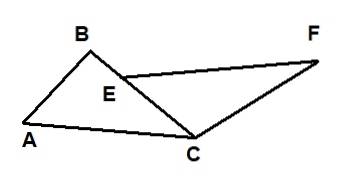
Alors la longueur du segment BE est égale à:
(i) 5
(ii) 3
(iii) 4
(iv) 2
(v) 6
Solution
Comme les deux triangles ont un côté d'égale longueur AC = EF compris entre les angles égaux ∡BAC = ∡CEF et ∡BCA = ∡CFE, on peut dire que les deux triangles sont congruents par le critère ALA.
Autrement dit, ΔBAC ≡ ΔCEF, nous devons donc:
BA = CE = AB = 6
BC = CF = 10
AC = EF
Mais le segment à calculer est BE = BC - EC = 10 - 6 = 4.
La bonne réponse est donc (iii).
- Exercice 2
Trois triangles sont illustrés dans la figure ci-dessous. On sait également que les deux angles indiqués mesurent 80º chacun et que les segments AB = PD et AP = CD. Trouvez la valeur de l'angle X indiqué sur la figure.
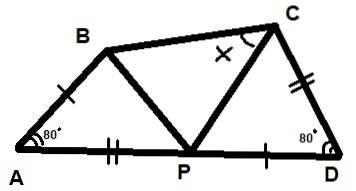
Solution
Vous devez appliquer les propriétés des triangles, qui sont détaillées étape par étape.
Étape 1
En partant du critère de congruence du triangle LAL, on peut affirmer que les triangles BAP et PDC sont congruents:
ΔBAP ≡ ΔPDC
Étape 2
Ce qui précède conduit à affirmer que BP = PC, donc le triangle ΔBPC est isocèle et ∡PCB = ∡PBC = X.
Étape 3
Si nous appelons l'angle BPC γ, il s'ensuit que:
2x + γ = 180 °
Étape 4
Et si on appelle les angles APB et DCP β et α les angles ABP et DPC, on a:
α + β + γ = 180º (puisque APB est un angle plan).
Étape 5
De plus, α + β + 80º = 180º par la somme des angles internes du triangle APB.
Étape 6
En combinant toutes ces expressions, nous avons:
α + β = 100º
Étape 7
Et par conséquent:
γ = 80 °.
Étape 8
Enfin, il s'ensuit que:
2X + 80 ° = 180 °
Avec X = 50º.
Les références
- Baldor, A. 1973. Géométrie plane et spatiale. Culturelle d'Amérique centrale.
- Fondation CK-12. Polygones congruents. Récupéré de: ck 12.org.
- Profitez des maths. Définitions: Rayon (polygone). Récupéré de: gustolasmatematicas.com.
- Référence ouverte mathématique. Test des polygones pour la congruence. Récupéré de: mathopenref.com.
- Wikipédia. Congruence (géométrie). Récupéré de: es.wikipedia.org.
- Zapata, F. Triangles, histoire, éléments, classification, propriétés. Récupéré de: lifeder.com.



Personne n'a encore commenté ce post.