Loi de Gauss

Quelle est la loi de Gauss?

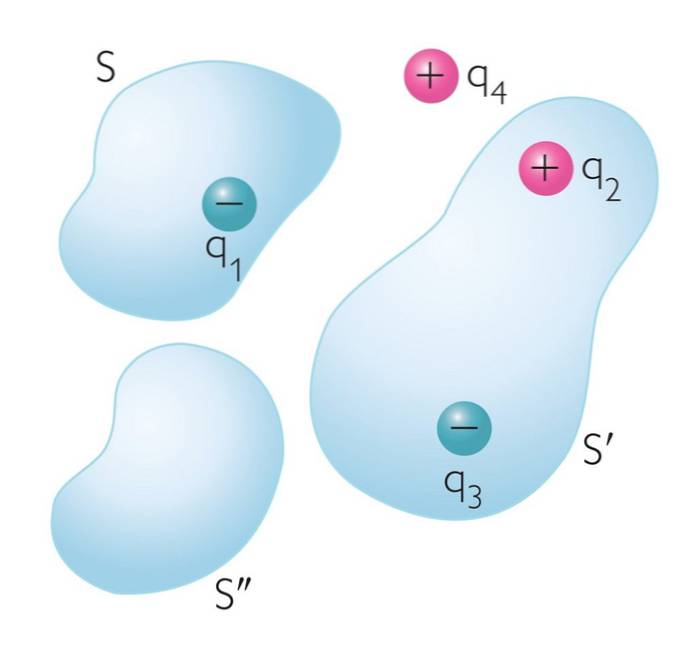
La loi de Gauss établit que le flux de champ électrique à travers une surface fermée imaginaire est proportionnel à la valeur de charge nette des particules trouvées à l'intérieur de ladite surface.

Dénotant le flux électrique à travers une surface fermée comme Φ_ET et la charge nette entourée par la surface par Q_enc, puis la relation mathématique suivante est établie:

Φ_ET = c ∙ Q_enc

Où c est la constante de proportionnalité.

Explication de la loi de Gauss

Pour comprendre la signification de la loi de Gauss, il est nécessaire d'expliquer les concepts impliqués dans son énoncé: charge électrique, champ électrique et champ électrique circulent à travers une surface..

Charge électrique

La charge électrique est l'une des propriétés fondamentales de la matière. Un objet chargé peut avoir l'un des deux types de charge: positive ou négative, bien que normalement les objets soient neutres, c'est-à-dire qu'ils ont la même quantité de charge négative que positive..

Deux objets chargés du même type se repoussent même lorsqu'il n'y a pas de contact entre eux et qu'ils sont dans le vide. Au contraire, lorsque chacun des corps a des charges d'un signe différent, alors ils s'attirent. Ce type d'interaction à distance est appelé interaction électrique..

Dans le système international d'unités SI, la charge électrique est mesurée en coulombs (C). Le porteur de charge élémentaire négative est le électron avec charge de -1,6 x 10^-19C et le porteur de charge élémentaire positif est le proton avec une valeur de charge +1,6 x 10^-19C. Les corps généralement chargés ont entre dix^-9C Oui dix^-3C.

Champ électrique

Un corps chargé électriquement modifie l'espace dans son environnement, le remplissant de quelque chose d'invisible appelé champ électrique. Pour savoir que ce champ est présent, il faut une charge de point de test positive.

Si la charge d'essai est placée dans un endroit où il y a un champ électrique, une force apparaît dessus dans une certaine direction, qui est la même que celle du champ électrique. L'intensité du champ est la force sur la charge de test divisée par la quantité de charge sur la charge de test. Puis les unités du champ électrique ET dans le système international d'unités sont newton Entrez coulomb: [E] = N / C.

Les charges ponctuelles positives produisent un champ radial vers l'extérieur, tandis que les charges négatives produisent un champ radialement vers l'intérieur. De plus, le champ produit par une charge ponctuelle décroît avec l'inverse du carré de la distance à ladite charge.

Lignes de champ électrique

Michael Faraday (1791 - 1867) a été le premier à avoir une image mentale du champ électrique, l'imaginant comme des lignes qui suivent la direction du champ. Dans le cas d'une charge ponctuelle positive, ces lignes sont radiales en partant du centre vers l'extérieur. Là où les lignes sont plus rapprochées, le champ est plus intense et moins intense là où elles sont plus éloignées.

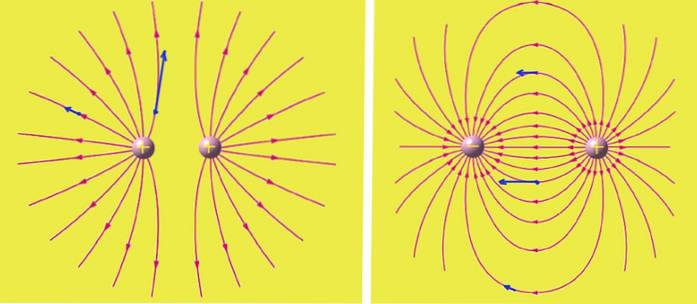
Les charges positives sont les sources d'où émergent les lignes de champ électrique, tandis que les charges négatives sont les puits des lignes..

Les lignes de champ électrique ne se referment pas sur elles-mêmes. Dans un ensemble de charges, les lignes quittent les charges positives et entrent les charges positives, mais elles peuvent aussi atteindre ou venir de l'infini.

Ils ne se croisent pas non plus et en chaque point de l'espace le vecteur de champ électrique est tangent à la ligne de champ et proportionnel à la densité des lignes à cet endroit..

Flux de champ électrique

Les lignes de champ électrique ressemblent aux lignes de courant d'une rivière qui coule doucement, d'où le concept d'écoulement de champ électrique est né..

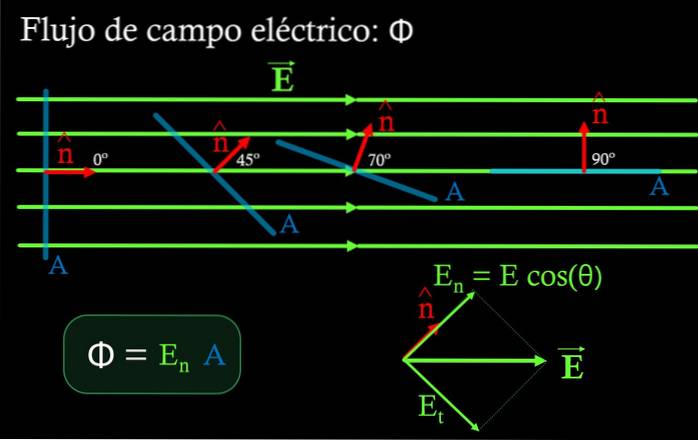
Dans une région où le champ électrique est uniforme, le flux Φ à travers une surface plane est le produit de la composante normale du champ E_n à cette surface, multipliée par la superficie À de la même:

Φ = E_n ∙ A

Composant E_n est obtenu en multipliant l'amplitude du champ électrique par le cosinus de l'angle formé entre le champ et le vecteur normal unitaire à la surface À. (voir figure 4).

Applications de la loi de Gauss

La loi de Gauss peut être appliquée pour déterminer le champ électrique produit par des distributions de charge avec un haut degré de symétrie.

Champ électrique d'une charge ponctuelle

Une charge ponctuelle produit un champ électrique radial qui est sortant si la charge est positive et entrante dans le cas contraire..

En choisissant comme surface gaussienne une sphère imaginaire de rayon R et concentrique à la charge Q, en tous points de la surface de ladite sphère, le champ électrique est de magnitude égale et sa direction est toujours normale à la surface. Donc, dans ce cas, le flux de champ électrique est le produit de la magnitude du champ et de la surface totale de la surface sphérique:

Φ = E ∙ A = E ∙ 4πR^deux

D'autre part, la loi de Gauss stipule que: Φ = c ∙ Q, étant la constante de proportionnalité c. Lorsque vous travaillez dans les unités du système de mesure international, la constante c est l'inverse de la permittivité du vide, et la loi de Gauss est formulée comme ceci:

Φ = (1 / ε_{ou alors}) ∙ Q

En incorporant le résultat obtenu pour l'écoulement vers la loi de Gauss, on a:

E ∙ 4πR^deux = (1 / ε_{ou alors}) ∙ Q

Et pour l'ampleur de ET résultat:

E = (1 / 4πε_{ou alors}) ∙ (Q / R^deux)

Ce qui est parfaitement en accord avec la loi de Coulomb du champ électrique d'une charge ponctuelle.

Exercices

Exercice 1

Deux charges ponctuelles se trouvent arbitrairement dans une surface gaussienne S. L'un d'eux est connu pour avoir une valeur de +3 nC (3 nano-coulomb). Si le flux de champ électrique net à travers la surface gaussienne est de 113 (N / C) m^deux, Quelle sera la valeur de l'autre charge?

Solution

La loi de Gauss stipule que

Φ_ET = (1 / ε_{ou alors}) ∙ Q_enc

Par conséquent, la charge nette incluse est:

Q_enc = Φ_ET ∙ ε_{ou alors}

Remplacer les résultats des données:

Q_enc = 113 (N / C) m^deux ∙ 8,85 x 10^-12 (C^deux m^-deux N^-1) = 1 x 10^-9 C = 1 nC.

Mais Q_enc = + Q - q, où la charge positive a une valeur connue de +3 nC, donc la charge sera nécessairement de -2 nC.

Exercice 2

Sur la figure 2, il y a un arrangement (à gauche) de deux charges positives, chacune avec une valeur + q et un autre arrangement (à droite) avec une charge + q et l'autre -q. Chaque arrangement est enfermé dans une boîte imaginaire avec tous ses bords de 10 cm. Si | q | = 3 μC, trouvez le flux de champ électrique net à travers la boîte pour chaque arrangement.

Solution

Dans le premier arrangement, le débit net est:

Φ_ET = (1 / ε_{ou alors}) ∙ (+ q + q) = 678000 (N / C) m^deux

Dans l'agencement de droite, le flux net à travers la boîte imaginaire contenant la paire de charges est nul..

Les références

1. Cosenza, M. Electromagnétisme. Université des Andes.
2. Díaz, R. Electrodynamics: notes de cours. Université nationale de Colombie.
3. Figueroa, D. (2005). Série: Physique pour la science et l'ingénierie. Volume 6. Electromagnétisme. Edité par Douglas Figueroa (USB).
4. Jackson, J. D. Electrodynamique classique. 3e. Ed. Wiley.
5. Tarazona, C. Introduction à l'électrodynamique. Éditorial Université Manuela Beltrán.