
Mouvement relatif en une dimension, en deux dimensions, exercices
le mouvement relatif d'une particule ou d'un objet est celui qui est observé par rapport à un point de référence particulier que l'observateur a choisi, qui peut être fixe ou en mouvement. La vitesse fait toujours référence à un système de coordonnées utilisé pour la décrire.
Par exemple, le passager d'une voiture en mouvement et qui se déplace confortablement endormi dans son siège est au repos par rapport au conducteur, mais pas pour un observateur debout sur le trottoir qui voit passer la voiture..

Alors le mouvement est toujours relatif, mais il arrive qu'en général le système de coordonnées ou de référence soit choisi ayant son origine dans la Terre ou le sol, lieu considéré comme stationnaire. De cette manière, le souci est centré sur la description du mouvement de l'objet étudié..
Est-il possible de décrire la vitesse du copilote endormi par rapport à un passager voyageant dans une autre voiture? La réponse est oui. Il y a liberté de choisir la valeur de (xou alors, Ouiou alors, zou alors): l'origine du référentiel. La sélection est arbitraire et dépend de la préférence de l'observateur, ainsi que de la facilité qu'elle offre pour résoudre le problème..
Index des articles
- 1 Mouvement relatif dans une dimension
- 1.1 - Exemple travaillé 1
- 2 Mouvement relatif en deux et trois dimensions
- 2.1 -Exercice résolu 2
- 2.2 - Exercice résolu 3
- 3 Références
Mouvement relatif dans une dimension
Lorsque le mouvement a lieu le long d'une ligne droite, les mobiles ont des vitesses dans le même sens ou dans le sens opposé, tous deux vus par un observateur debout sur Terre (T). L'observateur se déplace-t-il par rapport aux mobiles? Oui, avec la même vitesse qu'ils transportent, mais dans la direction opposée.
Comment un mobile se déplace-t-il par rapport à l'autre? Pour le savoir, les vitesses sont ajoutées de manière vectorielle.
-Exemple travaillé 1
En vous référant à la figure montrée, indiquez la vitesse relative de la voiture 1 par rapport à la voiture 2 dans chaque situation.
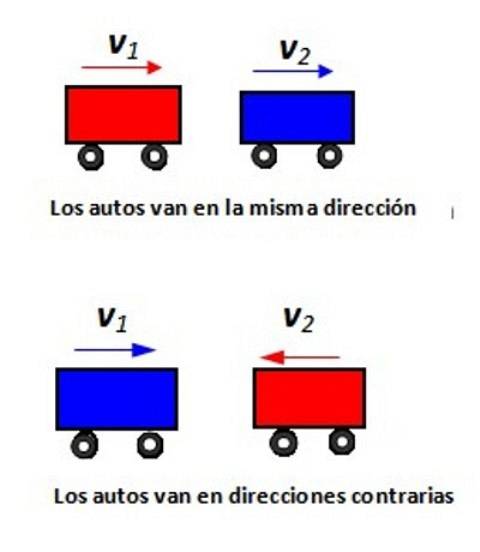
Solution
Nous attribuerons un signe positif aux vitesses à droite et un signe négatif à gauche. Si un mobile va vers la droite à 80 km / h, un passager sur ce mobile voit l'observateur sur Terre se déplacer à - 80 km / h.
Supposons que tout se passe le long de l'axe des x. Dans la figure suivante, la voiture rouge se déplace à +100 km / h (vue de T) et est sur le point de dépasser la voiture bleue roulant à +80 km / h (vue également de T). À quelle vitesse un passager de la voiture bleue s'approche-t-il de la voiture rouge?
Les étiquettes sont: v 1/2 vitesse de la voiture 1 par rapport à la voiture 2, v1 / T vitesse de la voiture par rapport à T, vT / 2 vitesse de T par rapport à 2. Addition de vecteur:
v1/2 = v1 / T + vT / 2 = (+100 km / h - 80 km / h) X= 20 km / h X
On peut se passer de la notation vectorielle. Remarquez les indices: en multipliant les deux à droite, vous devriez obtenir celui de gauche.
Et quand ils vont dans l'autre sens? Maintenant v1 / T = + 80 km / h et v2 / T = -100 km / h, donc vT / 2 = + 100 km / h. Le passager de la voiture bleue verra l'approche de la voiture rouge:
v1/2 = v1 / T + vT / 2 = +80 km / h +100 km / h = 180 km / h
Mouvement relatif en deux et trois dimensions
Dans le schéma suivant, r est la position du plan vu du système X y Z, r'est la position du système X y Z' Oui R est la position du système avec une prime par rapport au système sans prime. Les trois vecteurs forment un triangle dans lequel R + r'= r, donc r'= r - R.
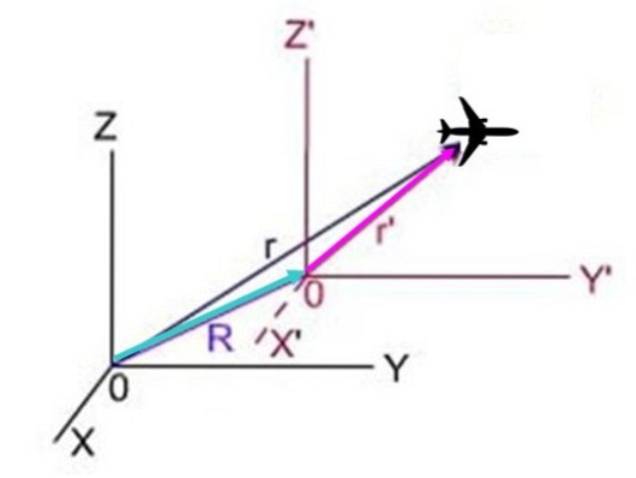
Puisque la dérivée par rapport au temps de la position est précisément la vitesse, il en résulte:
v'= v - ou alors
Dans cette équation v'est la vitesse de l'avion par rapport au système X y Z', v est la vitesse par rapport au système X y Z Oui ou alors est la vitesse constante du système premier par rapport au système non amorcé.
-Exercice résolu 2
Un avion se dirige vers le nord avec une vitesse de 240 km / h. Soudain, le vent commence à souffler d'ouest en est à une vitesse de 120 km / selon la terre.
Trouver: a) La vitesse de l'avion par rapport au sol, b) La déviation subie par le pilote c) La correction que le pilote doit faire pour pouvoir viser directement le nord et la nouvelle vitesse par rapport au sol, une fois la correction a été faite.
Solution
a) Il y a les éléments suivants: plan (A), sol (T) et vent (V).
Dans le système de coordonnées dans lequel le nord est la direction + y et la direction ouest-est est + x, nous avons les vitesses données et leur étiquette respective (indices):
v UN V = 240 km / h (+Oui); v V / T = 120 km / h (+X); v À = ?
La somme vectorielle appropriée est:
v À = v UN V + v V / T = 240 km / h (+Oui) + 120 km / h (+X)
La magnitude de ce vecteur est: v À = (240 deux+ 120deux)1/2 km / h = 268,3 km / h
b) θ = arctg (v UN V / v V / T) = arctg (240/120) = 63,4 ° au nord de l'est ou 26,6 ° au nord-est.
c) Pour continuer vers le nord avec ce vent, vous devrez pointer la proue de l'avion vers le nord-ouest, de sorte que le vent vous pousse directement vers le nord. Dans ce cas, la vitesse de l'avion vu du sol sera dans la direction + y, tandis que la vitesse de l'avion par rapport au vent sera du nord-ouest (elle ne doit pas nécessairement être de 26,6 °).
Par théorème de Pythagore:
v À = (240 deux- 120deux)1/2 km / h = 207,8 km / h
α = arctg (v V / T / v À ) = arctg (120 / 207.8) = 30º Nord-Ouest
-Exercice résolu 3
Il faut 2 minutes à une personne pour descendre un escalator fixe. Si l'échelle fonctionne, il faut 1 minute à la personne pour descendre tout en restant immobile. Combien de temps faut-il à la personne pour descendre avec l'échelle en marche?
Solution
Il y a trois éléments à considérer: la personne (P), l'échelle (E) et le sol (S), dont les vitesses relatives sont:
vP / E : vitesse de la personne par rapport à l'échelle; vC'EST: vitesse de l'échelle par rapport au sol; vP / S: vitesse de la personne par rapport au sol.
Vu du sol par un observateur fixe, la personne qui descend l'échelle (E) a une vitesse v P / S donné par:
v P / S = vP / E + vC'EST
La direction positive descend l'échelle. Être t le temps qu'il faut pour descendre et L la distance. L'amplitude de la vitesse de la personne v P / S c'est:
vP / S = L / t
t1 est le temps qu'il faut pour descendre avec l'échelle arrêtée: v P / E = L / t1
Et Tdeux celui qui vous fait descendre encore sur l'escalier mobile: v C'EST = L / tdeux
Combinaison des expressions:
L / t = L / t1 + L / tdeux
Substituer des valeurs numériques et résoudre t:
1 / t = 1 / t1 + 1 / tdeux = 1/2 + 1/1 = 1,5
Donc t = 1 / 1,5 minute = 40 secondes.
Les références
- Bauer, W. 2011. Physique pour l'ingénierie et les sciences. Volume 1. Mc Graw Hill. 84-88.
- Figueroa, D. Série de physique pour les sciences et l'ingénierie. Volume 3. Édition. Cinématique. 199-232.
- Giancoli, D. 2006. Physique: principes avec applications. 6e. Ed. Prentice Hall. 62-64.
- Mouvement relatif. Récupéré de: courses.lumenlearning.com
- Wilson, J. 2011. Physique 10. Pearson Education. 166-168.



Personne n'a encore commenté ce post.