
Concept d'ondes linéaires, caractéristiques, exemples
le ondes linéaires sont ceux dans lesquels le principe de superposition est applicable, c'est-à-dire ceux dans lesquels la forme d'onde et son évolution spatio-temporelle peuvent être réalisées comme somme de solutions de base, par exemple de type harmonique. Toutes les ondes ne sont pas conformes au principe de superposition, celles qui ne le sont pas sont appelées ondes non linéaires.
Le nom «linéaire» vient du fait que les ondes linéaires satisfont toujours une équation différentielle en dérivées partielles, dans laquelle tous les termes qui impliquent la variable dépendante ou ses dérivées sont élevés à la première puissance.

D'autre part, les ondes non linéaires satisfont les équations d'onde qui ont des termes quadratiques ou des degrés supérieurs dans la variable dépendante ou dans ses dérivées..
Les ondes linéaires sont parfois confondues avec les ondes longitudinales, qui sont celles dans lesquelles la vibration se produit dans la même direction de propagation, que les ondes sonores.
Mais les ondes longitudinales, ainsi que les ondes transversales, peuvent à leur tour être linéaires ou non linéaires en fonction, entre autres facteurs, de l'amplitude de la perturbation initiale et du milieu dans lequel elles se propagent..
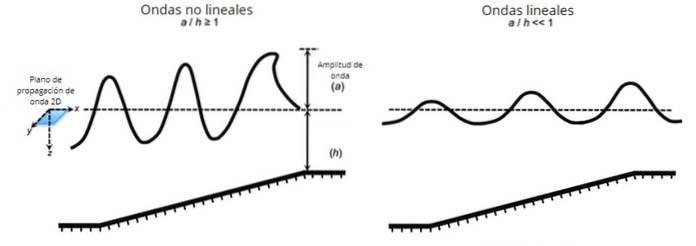
Il arrive généralement que lorsque la perturbation initiale est de faible amplitude, l'équation qui décrit la propagation de l'onde est linéaire ou peut être linéarisée par certaines approximations, bien que ce ne soit pas toujours le cas..
Index des articles
- 1 Équation différentielle en ondes linéaires
- 1.1 Solutions de l'équation différentielle
- 2 Ondes linéaires dispersives et non dispersives
- 2.1 Ondes non dispersives
- 2.2 Ondes dispersives
- 3 Exemples d'ondes linéaires
- 3.1 Ondes électromagnétiques
- 3.2 L'équation de Schrödinger
- 3.3 Vagues en eau profonde
- 3.4 Le son
- 3.5 Vagues dans une corde tendue
- 4 Références
Équation différentielle en ondes linéaires
Dans un milieu linéaire, une forme d'onde limitée dans l'espace et dans le temps peut être représentée par la somme des fonctions d'onde de type sinus ou cosinus de différentes fréquences et longueurs d'onde en utilisant la série de Fourier.
Les ondes linéaires ont toujours associé une équation différentielle de type linéaire, dont la solution représente la prédiction de ce que sera la perturbation aux instants ultérieurs d'une perturbation initiale localisée spatialement à l'instant initial.
L'équation d'onde linéaire classique, dans une seule dimension spatiale, dont les solutions sont des ondes linéaires est:
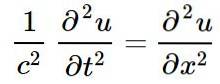
Dans l'équation ci-dessus ou alors représente la perturbation d'une certaine quantité physique à la position X et dans l'instant t, c'est-à-dire ou alors est une fonction de X Oui t:
u = u (x, t)
Par exemple, s'il s'agit d'une onde sonore dans l'air, ou alors peut représenter la variation de la pression par rapport à sa valeur sans perturber.
Dans le cas d'une onde électromagnétique, u représente le champ électrique ou le champ magnétique oscillant perpendiculairement à la direction de propagation.
Dans le cas d'une corde tendue, ou alors représente le déplacement transversal par rapport à la position d'équilibre de la corde, comme le montre la figure suivante:

Solutions de l'équation différentielle
S'il y a deux ou plusieurs solutions de l'équation différentielle linéaire, alors chaque solution multipliée par une constante sera une solution, de même que leur somme.
Contrairement aux équations non linéaires, les équations d'ondes linéaires admettent des solutions harmoniques du type:
ou alors1= A⋅sen (k⋅x - ω⋅t) Oui ou alorsdeux= A⋅sen (k⋅x + ω⋅t)
Cela peut être vérifié par simple substitution dans l'équation d'onde linéaire.
La première solution représente une onde progressive se déplaçant vers la droite, tandis que la seconde solution vers la gauche rapidement c = ω / k.
Les solutions harmoniques sont caractéristiques des équations d'ondes linéaires.
D'autre part, la combinaison linéaire de deux solutions harmoniques est également une solution de l'équation d'onde linéaire, par exemple:
u = A1 cos (k1⋅x - ω1⋅t) + Adeux sen (kdeux⋅x - ωdeux⋅t) est la solution.
La caractéristique la plus pertinente des ondes linéaires est que toute forme d'onde, aussi complexe soit-elle, peut être obtenue par une sommation d'ondes harmoniques simples en sinus et cosinus:
u (x, t) = A0 + ∑n Àn cos (kn⋅x - ωn⋅t) + ∑m Bm sen (km⋅x - ωm⋅t).
Ondes linéaires dispersives et non dispersives
Dans l'équation d'onde linéaire classique, c représente la vitesse de propagation de l'impulsion.
Ondes non dispersives
Dans les cas où c est une valeur constante, par exemple des ondes électromagnétiques dans le vide, puis une impulsion à l'instant initial t = 0 Façonner f (x) se propage selon:
u (x, t) = f (x - c⋅t)
Sans subir aucune distorsion. Lorsque cela se produit, le milieu est dit non dispersif..
Ondes dispersives
Cependant, dans les milieux dispersifs, la vitesse de propagation c peut dépendre de la longueur d'onde λ, soit: c = c (λ).
Les ondes électromagnétiques sont dispersives lorsqu'elles traversent un milieu matériel. De plus, les ondes de surface de l'eau se déplacent à des vitesses différentes en fonction de la profondeur de l'eau.
La vitesse à laquelle une onde harmonique du type A⋅sen (k⋅x - ω⋅t) c'est ω / k = c y s'appelle la vitesse de phase. Si le milieu est dispersif, alors c est fonction du nombre d'onde k: c = c (k), où k est lié à la longueur d'onde par k = 2π / λ.
Rapports de dispersion
La relation entre la fréquence et la longueur d'onde s'appelle le rapport de dispersion, qu'exprimé en termes de fréquence angulaire ω et le nombre d'onde k c'est: ω = c (k) ⋅k.
Certaines relations de dispersion caractéristiques des ondes linéaires sont les suivantes:
Dans les vagues océaniques où la longueur d'onde (distance entre les crêtes) est bien supérieure à la profondeur H, mais comme son amplitude est bien inférieure à la profondeur, la relation de dispersion est:
ω = √ (gH) ⋅k
De là, on conclut qu'ils se propagent à vitesse constante √ (gH) (milieu non dispersif).
Mais les vagues dans les eaux très profondes sont dispersives, car leur rapport de dispersion est:
ω = √ (g / k) ⋅k
Cela signifie que la vitesse de phase ω / k est variable et dépend du nombre d'onde et donc de la longueur d'onde de l'onde.
Vitesse du groupe
Si deux ondes linéaires harmoniques se chevauchent mais avancent à des vitesses différentes, alors la vitesse du groupe (c'est-à-dire du paquet d'ondes) ne correspond pas à la vitesse de phase.
Vitesse du groupe vg est défini comme la dérivée de la fréquence par rapport au nombre d'onde dans la relation de dispersion: vg = ω '(k).
La figure suivante montre la superposition ou la somme de deux ondes harmoniques ou alors1= A⋅sen (k1⋅x - ω1⋅t) Oui ou alorsdeux= A⋅sen (kdeux⋅x - ωdeux⋅t) voyager à des vitesses différentes v1= ω1/ k1 Oui vdeux= ωdeux/ kdeux. Notez comment la vitesse du groupe est différente de la vitesse de phase, dans ce cas, la vitesse du groupe est ∆ω / ∆k.
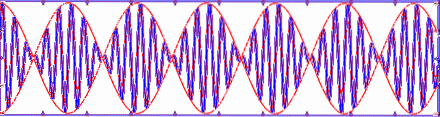
En fonction du rapport de dispersion, il peut même arriver que la vitesse de phase et la vitesse de groupe, en ondes linéaires, aient des directions opposées..
Exemples d'ondes linéaires
Ondes électromagnétiques

Les ondes électromagnétiques sont des ondes linéaires. Son équation d'onde est dérivée des équations de l'électromagnétisme (équations de Maxwell) qui sont également linéaires.
L'équation de Schrödinger
C'est l'équation qui décrit la dynamique des particules à l'échelle atomique, où les caractéristiques de l'onde sont pertinentes, par exemple le cas des électrons dans l'atome.
Donc la "onde électronique" ou fonction d'onde comme on l'appelle aussi, est une onde linéaire.
Vagues en eau profonde
Les ondes linéaires sont également celles dont l'amplitude est bien inférieure à la longueur d'onde et la longueur d'onde bien supérieure à la profondeur. Les vagues en eau profonde suivent la théorie linéaire (connue sous le nom de théorie des vagues d'Airy).
Cependant, la vague qui s'approche du rivage et forme la crête caractéristique du curling (et que les surfeurs adorent) est une vague non linéaire..
Sonner
Le son étant une petite perturbation de la pression atmosphérique, il est considéré comme une onde linéaire. Cependant, l'onde de choc d'une explosion ou le front d'onde d'un avion supersonique sont des exemples typiques d'onde non linéaire..
Vagues sur une corde tendue
Les ondes qui se propagent à travers une corde tendue sont linéaires, tant que la pulsation initiale est de faible amplitude, c'est-à-dire que la limite élastique de la corde n'est pas dépassée..
Les ondes linéaires dans les cordes sont réfléchies à leurs extrémités et se chevauchent, donnant lieu à des ondes stationnaires ou à des modes de vibration qui donnent les tons harmoniques et sous-harmoniques caractéristiques des instruments à cordes..
Les références
- Griffiths G et Schiesser W. Ondes linéaires et non linéaires. Récupéré de: sholarpedia.org.
- Whitham G.B. (1999) "Ondes linéaires et non linéaires". Wiley.
- Wikipédia. Ondes non linéaires. Récupéré de: es.wikipedia.com
- Wikipédia. Acoustique non linéaire. Récupéré de: en.wikipedia.com
- Wikipédia. Vagues. Récupéré de: en.wikipedia.com
- Wikiwaves. Ondes non linéaires. Récupéré de: wikiwaves.org



Personne n'a encore commenté ce post.