
Expression mathématique des ondes unidimensionnelles et exemples
le ondes unidimensionnelles Ce sont ceux qui se propagent dans une seule direction, que la vibration se produise ou non dans la même direction de propagation. Un bon exemple d'entre eux est la vague qui traverse une corde tendue comme celle d'une guitare..
Dans une vague plate traverser, les particules vibrent dans une direction verticale (elles montent et descendent, voir la flèche rouge sur la figure 1), mais c'est unidimensionnel car la perturbation se déplace dans une seule direction, suivant la flèche jaune.

Les ondes unidimensionnelles apparaissent assez fréquemment dans la vie quotidienne. La section suivante en décrit quelques exemples ainsi que des ondes qui ne sont pas unidimensionnelles, pour établir clairement les différences.
Index des articles
- 1 Exemples d'ondes unidimensionnelles et d'ondes non unidimensionnelles
- 1.1 Ondes unidimensionnelles
- 1.2 Ondes non unidimensionnelles
- 2 Expression mathématique d'une onde unidimensionnelle
- 2.1 Équation d'onde unidimensionnelle
- 2.2 Exemple travaillé
- 3 Références
Exemples d'ondes unidimensionnelles et d'ondes non unidimensionnelles
Ondes unidimensionnelles
Voici quelques exemples d'ondes unidimensionnelles facilement observables:
- Une impulsion sonore qui traverse une barre droite, car c'est une perturbation qui se propage sur toute la longueur de la barre.
- Une vague traversant un canal d'eau, même si le déplacement de la surface de l'eau n'est pas parallèle au canal.
- Les ondes qui se propagent sur une surface ou à travers un espace tridimensionnel peuvent également être unidimensionnelles, à condition que leurs fronts d'onde soient des plans parallèles les uns aux autres et se déplacent dans une seule direction..
Ondes non unidimensionnelles
Un exemple d'onde non unidimensionnelle se trouve dans les vagues qui se forment sur une surface d'eau immobile lorsqu'une pierre tombe. C'est une onde bidimensionnelle avec un front d'onde cylindrique.

Un autre exemple d'onde non unidimensionnelle est l'onde sonore qu'un pétard génère en explosant à une certaine hauteur. C'est une onde tridimensionnelle avec des fronts d'onde sphériques.
Expression mathématique d'une onde unidimensionnelle
La manière la plus générale d'exprimer une onde unidimensionnelle qui se propage sans atténuation dans la direction positive de l'axe X et avec rapidité v est, mathématiquement:
y (x, t) = f (x - v.t)
Dans cette expression Oui représente la perturbation de la position X à l'instant t. La forme de l'onde est donnée par la fonction F. Par exemple, la fonction d'onde illustrée à la figure 1 est: y (x, t) = cos (x - v t) et l'image d'onde correspond à l'instant t = 0.
Une onde comme celle-ci, décrite par une fonction cosinus ou sinusoïdale, est appelée onde harmonique. Bien que ce ne soit pas la seule forme d'onde qui existe, elle est de la plus haute importance, car toute autre onde peut être représentée comme une superposition ou une somme d'ondes harmoniques. Il s'agit du connu Théorème de Fourier, tellement utilisé pour décrire des signaux de toutes sortes.
Lorsque l'onde se déplace dans la direction négative de l'axe des x, elle change simplement v pour -v en argument, laissant:
y (x, t) = g (x + v t)
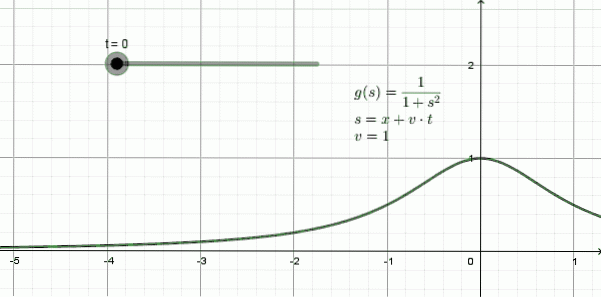
La figure 3 montre l'animation d'une onde se déplaçant vers la gauche: c'est une forme appelée fonction Lorentziana et elle l'expression mathématique est:
y (x, t) = 1 / (1 + (x + 1⋅t)deux
Dans cet exemple, la vitesse de propagation est v = 1, -une unité d'espace pour chaque unité de temps-.
Équation d'onde unidimensionnelle
L'équation d'onde est une équation dérivée partielle dont la solution est bien entendu une onde. Il établit la relation mathématique entre la partie spatiale et la partie temporelle de celle-ci, et a la forme:

Exemple travaillé
Voici l'expression générale y (x, t) pour une onde harmonique:
y (x, t) = A⋅cos (k⋅x ± ω⋅t + θo)
a) Décrivez la signification physique des paramètres A, k, ω Oui θo.
b) Quelle signification ont les signes ± dans l'argument cosinus?
c) Vérifiez que l'expression donnée est bien la solution de l'équation d'onde de la section précédente et trouvez la vitesse v propagation.
Solution à)
Les caractéristiques de la vague se retrouvent dans les paramètres suivants:
-À représente le amplitude ou "hauteur des vagues".
-Ce qui est en numéro d'onde et est lié à la longueur d'onde λ à travers k = 2π / λ.
-ω est le ffréquence angulaire et est lié à la période T oscillation d'onde par
ω = 2π / T.
-θo est le phase initiale, qui est lié au point de départ de la vague.
Solution b)
Un signe négatif est pris si l'onde se déplace dans la direction positive de l'axe X et un signe positif dans le cas contraire..
Solution c)
Vérifiez que l'expression donnée est une solution de l'équation d'onde est simple: la dérivée partielle de la fonction est prise y (x, t) par rapport à x deux fois, partiellement re-dérivé par rapport à t deux fois, puis combiner les deux résultats pour obtenir une égalité:
Dérivée seconde par rapport à x: ∂deuxy / ∂xdeux= -Kdeux. À⋅cos (k⋅x ± ω⋅t + θo)
Dérivée seconde par rapport à t: ∂deuxy / ∂tdeux= -Ωdeux. À⋅cos (k⋅x ± ω⋅t + θo)
Ces résultats sont substitués dans l'équation d'onde:
-kdeux. À⋅cos (k⋅x ± ω⋅t + θo) = (1 / vdeux) (-ωdeux. À⋅cos (k⋅x ± ω⋅t + θo))
Tellement de À comme les cosinus sont simplifiés, puisqu'ils apparaissent des deux côtés de l'égalité et que l'argument du cosinus est le même, donc l'expression se réduit à:
-kdeux = (1 / vdeux) (-ωdeux)
Ce qui permet d'obtenir une équation pour v en termes de ω Oui k:
vdeux = ωdeux / kdeux
v = ± ω / k
Les références
- E-éducatif. Équation des ondes harmoniques unidimensionnelles. Récupéré de: e-ducativa.catedu.es
- Le coin de la physique. Classes de vagues. Récupéré de: fisicaparatontos.blogspot.com.
- Figueroa, D. 2006. Vagues et physique quantique. Série: Physique pour la science et l'ingénierie. Edité par Douglas Figueroa. Université Simon Bolivar. Caracas, Venezuela.
- Laboratoire de physique Mouvement des vagues. Récupéré de: fisicalab.com.
- Peirce, A. Conférence 21: L'équation d'onde unidimensionnelle: la solution de D'Alembert. Récupéré de: ubc.ca.
- Équation de vague. Récupéré de: en.wikipedia.com


Personne n'a encore commenté ce post.