
Qu'est-ce que l'épistasie? (Avec des exemples)
La épistasie, en génétique, c'est l'étude de l'interaction entre les différents gènes qui codent pour le même caractère. Autrement dit, c'est la manifestation d'un trait qui découle de l'interaction entre les allèles de gènes à différents loci.
Lorsque nous parlons des relations qui établissent des allèles du même gène, nous nous référons aux relations alléliques. C'est-à-dire aux allèles du même locus ou allèles allélomorphes. Ce sont les interactions bien connues de dominance complète, de dominance incomplète, de codominance et de létalité entre les allèles du même gène..
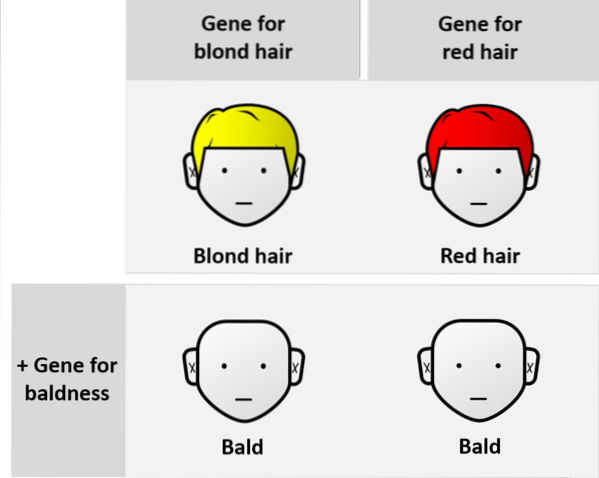
Dans les relations entre allèles de différents loci, au contraire, on parle d'allèles non allélomorphes. Ce sont les soi-disant interactions génétiques, qui sont en quelque sorte toutes épistatiques.
L'épistase permet d'analyser si l'expression d'un gène détermine l'expression d'un autre. Dans un tel cas, un tel gène serait épistatique sur le second; le second serait hypostatique sur le premier. L'analyse des épistasies permet également de déterminer l'ordre dans lequel agissent les gènes qui définissent le même phénotype.
L'épistasie la plus simple analyse comment deux gènes différents interagissent pour conférer le même phénotype. Mais évidemment, cela peut être beaucoup plus de gènes.
Pour l'analyse de l'épistasie simple, nous nous baserons sur les variations des proportions des croisements dihybrides classiques. Autrement dit, aux modifications du rapport 9: 3: 3: 1, et à elle-même.
Index des articles
- 1 Le rapport phénotypique classique 9: 3: 3: 1
- 2 Des écarts qui ne le sont pas
- 2.1 Le rapport 9: 3: 3: 1 (double épistasie dominante)
- 2.2 Le rapport 15: 1 (action génétique doublée)
- 2.3 Le rapport 13: 3 (suppression dominante)
- 2.4 Le rapport 9: 7 (épistasie récessive doublée)
- 3 Autres rapports phénotypiques épistatiques
- 4 Références
Le rapport phénotypique classique 9: 3: 3: 1
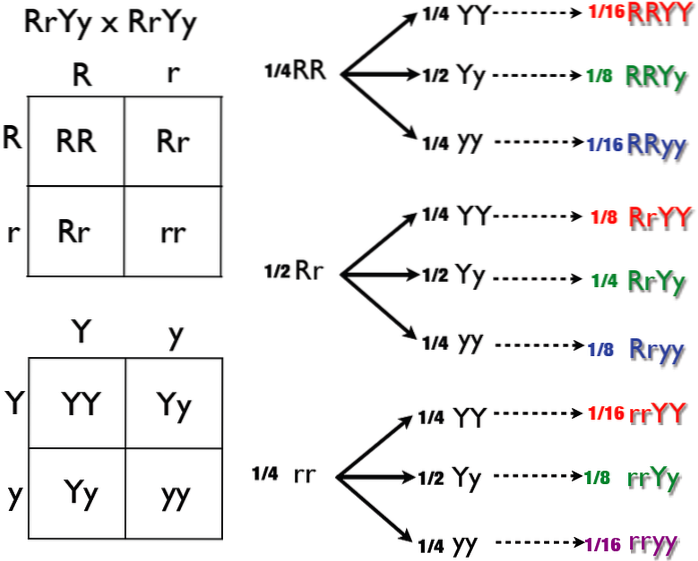
Cette proportion résulte de la combinaison de l'analyse d'héritage de deux caractères différents. Autrement dit, il est le produit de la combinaison de deux ségrégations phénotypiques indépendantes (3: 1) X (3: 1).
Lorsque Mendel analysait, par exemple, la stature de la plante ou la couleur de la graine, chaque caractère était séparé de 3 à 1. Lorsqu'il les analysait ensemble, même s'il s'agissait de deux caractères différents, chacun était séparé de 3 à 1. Autrement dit, ils étaient répartis indépendamment.
Cependant, lorsque Mendel a analysé les caractères par paires, ils ont abouti aux classes phénotypiques bien connues 9, 3, 3 et 1. Mais ces classes étaient des sommes de deux caractères. différent. Et jamais, aucun des deux personnages n'a affecté la façon dont l'autre s'est manifesté.
Des écarts qui ne le sont pas
Le précédent était l'explication de la proportion mendélienne classique. Par conséquent, ce n'est pas un cas d'épistasie. Epistasis étudie les cas d'hérédité du même caractère déterminés par plusieurs gènes.
Le cas précédent, ou deuxième loi de Mendel, concernait l'héritage de deux caractères différents. Ceux expliqués plus tard sont de vraies proportions épistatiques et n'impliquent que des allèles non allélomorphes..
Le rapport 9: 3: 3: 1 (double épistasie dominante)
Ce cas se trouve lorsque le même personnage présente quatre manifestations phénotypiques différentes dans un rapport de 9: 3: 3: 1. Par conséquent, il ne peut pas s'agir d'une interaction allélique (monogénique) comme celle qui conduit à l'apparition de quatre groupes sanguins différents dans le système ABO..
Prenons comme exemple le croisement entre un individu hétérozygote avec du sang de type A et un individu hétérozygote avec du sang de type B. jeÀje X jeBje. Cela nous donnerait un ratio 1: 1: 1: 1 d'individus jeÀje (Type A), jeÀjeB (Type AB), jeBje (Type B) e ii (Type O).
Au contraire, une véritable double relation épistatique dominante (9: 3: 3: 1) est observée sous la forme du crête de coq. Il existe quatre classes phénotypiques, mais dans un rapport 9: 3: 3: 1.
Deux gènes participent à sa détermination et à sa manifestation, appelons-les R Oui P. Quoi qu'il en soit, les allèles R Oui P montrer une domination complète sur les allèles r Oui p, respectivement.
De la traversée RrPp X RrPp on peut obtenir les classes phénotypiques 9 R_P_, 3 R_pp, 3 rrP_ et 1 rrpp. Le symbole "_" signifie que l'allèle peut être dominant ou récessif. Le phénotype associé reste le même.
La classe 9 R_P_ est représentée par des coqs à crête de noyer, 3 R_pp par des coqs à crête de rose. Les coqs à crête de pois seraient de classe 3 rrP_; ceux de la classe rrpp ont une simple crête.

Dans l'épistasie double dominante, chaque classe 3 résulte de l'effet de dominance du gène R ou P. La classe 9 est représentée par celle dans laquelle les allèles dominants R et P se manifestent. Enfin, dans la classe 1 rrpp, les allèles dominants sont absents. des deux gènes.
Le rapport 15: 1 (action génétique doublée)
Dans cette interaction épistatique, un gène ne supprime pas la manifestation d'un autre. Au contraire, les deux gènes codent pour la manifestation du même trait, mais sans effet additif..
Par conséquent, la présence d'au moins un allèle dominant de l'un ou l'autre des deux gènes de locus différents permet la manifestation du trait en classe 15. L'absence d'allèles dominants (la double classe récessive) détermine le phénotype de la classe 1.
Les produits des gènes participent à la manifestation de la couleur du grain de blé À je B. Autrement dit, l'un ou l'autre de ces produits (ou les deux) peut conduire à la réaction biochimique qui transforme le précurseur en pigment..
La seule classe qui n'en produit aucun est la classe 1 aabb. Par conséquent, les classes 9 A_B_, 3 A_bb et 3 aaB_ produiront des grains pigmentés, et la minorité restante ne produira pas.
Le rapport 13: 3 (suppression dominante)
On retrouve ici un cas de délétion dominante d'un gène (hypostatique) due à la présence d'au moins un allèle dominant de l'autre (épistatique). Autrement dit, formellement, un gène supprime l'action de l'autre..
S'il s'agit de la suppression dominante de D sur K, on aurait le même phénotype associé aux classes 9 D_K_, 3 D_kk et 1 ddkk. La classe 3 ddK_ serait la seule à présenter le trait non supprimé.
La classe double récessive s'ajoute aux classes 9 D_K_ et 3 D_kk car elle ne produit pas ce pour quoi le gène hypostatique K code. Non pas parce qu'elle est supprimée par D, qui de toute façon n'y est pas non plus, mais parce qu'elle ne produit pas K.
Ce rapport est parfois également appelé épistasie dominante et récessive. Le dominant est celui de K sur J / j. L'épistase récessive serait celle de jj sur K / k.
Par exemple, les fleurs de primevère doivent leur couleur à la manifestation de deux gènes. La Gen K qui code pour la production du pigment malvidine et du gène ré quels codes pour la suppression de la malvidine.
Juste des plantes ddKK ou alors ddKk (c'est-à-dire la classe 3 ddK_) produira de la malvidine et sera de couleur bleue. Tout autre génotype donnera naissance à des plantes aux fleurs turquoises.
Le rapport 9: 7 (épistasie récessive doublée)
Dans ce cas, la présence d'au moins un allèle dominant de chaque gène de la paire est nécessaire pour que le caractère se manifeste. Disons que ce sont les gènes C Oui P. Autrement dit, l'état récessif homozygote de l'un des gènes de la paire (DC ou alors pp) rend la manifestation du personnage impossible.
En d'autres termes, seule la classe 9 C_P_ a au moins un allèle dominant C et un allèle dominant P. Pour que le trait se manifeste, les produits fonctionnels des deux gènes doivent être présents.
Cette interaction est épistatique car le manque d'expression d'un gène empêche l'autre gène de se manifester. C'est double, car l'inverse est également vrai.
Un exemple classique qui illustre ce cas est celui des fleurs de pois. Les plantes CCpp et les plantes ccPP ils ont des fleurs blanches. Les hybrides CcPp des croisements entre eux présentent des fleurs violettes.
Si deux de ces plantes dihybrides sont croisées, nous obtiendrons la classe 9 C-P_, qui aura des fleurs violettes. Les classes 3 C_pp, 3 ccP_ et ccpp seront des fleurs blanches.

Autres rapports phénotypiques épistatiques
De la proportion proposée dans la deuxième loi de Mendel, nous avons d'autres cas supplémentaires qui méritent d'être mentionnés..
Nous appelons l'épistasie récessive au rapport 9: 4: 3 modifié pour une bonne raison. Lorsqu'un gène est homozygote pour le gène récessif, il évite l'expression de l'autre gène - même s'il est dominant.
Prenons par exemple l'épistasie récessive du génotype aa à propos de ceux du gène B. La classe 9 est la 9 A_B_ déjà reconnue. Pour la classe 4, à la classe 1 aabb, il faut ajouter ceux de la classe 3 aaB_, avec le même phénotype. La classe 3 serait celle de la classe 3 A_bb.
Dans l'interaction épistatique des gènes dupliqués, le rapport phénotypique observé est de 9: 6: 1. Tous les individus de la classe 9 A_B_ ont au moins un allèle de chaque gène À ou alors B. Ils ont tous le même phénotype.
Au contraire, dans les classes 3 A_bb et 3 aaBb, il n'y a que des allèles dominants de A ou B. Dans ce cas, il y a aussi un seul et même phénotype - mais différent des autres. Enfin, dans la classe 1 aabb, aucun allèle dominant de l'un des gènes n'est présent et représente un autre phénotype.
La classe peut-être la plus déroutante est l'épistasie dominante, qui montre le rapport phénotypique 12: 3: 1. Ici, la dominance de A (épistatique) sur B (hypostatique) fait que la classe 9 A-B_ rejoint la classe 3 A_bb.
Le phénotype de B ne se manifestera que lorsque A n'est pas présent dans la classe 3 aaB_. Le double aabb récessif de classe 1 ne se manifestera ni le phénotype associé au gène A / a ni avec le gène B / b.
Les autres rapports phénotypiques épistatiques qui n'ont pas de nom particulier sont 7: 6: 3, 3: 6: 3: 4 et 11: 5.
Les références
- Brooker, R. J. (2017). Génétique: analyse et principes. McGraw-Hill Higher Education, New York, NY, États-Unis.
- Goodenough, U. W. (1984) Génétique. W. B. Saunders Co. Ltd, Pkiladelphia, PA, États-Unis.
- Griffiths, A. J. F., Wessler, R., Carroll, S. B., Doebley, J. (2015). Une introduction à l'analyse génétique (11e éd.). New York: W. H. Freeman, New York, NY, États-Unis.
- Miko, I. (2008) Epistasis: Interaction génique et effets phénotypiques. Éducation à la nature 1: 197. nature.com
- White, D., Rabago-Smith, M. (2011). Associations génotype-phénotype et couleur des yeux humains. Journal of Human Genetics, 56: 5-7.
- Xie, J., Qureshi, A. A., Li., Y., Han, J. (2010) Groupe sanguin ABO et incidence du cancer de la peau. PLoS ONE, 5: e11972.
Personne n'a encore commenté ce post.