
Pavés caractéristiques, types (réguliers, irréguliers), exemples
Les en mosaïque sont des surfaces couvertes par une ou plusieurs figures appelées carrelage. Ils sont partout: dans les rues et les immeubles de toutes sortes. Les tesselles ou tuiles sont des pièces plates, généralement des polygones avec des copies congruentes ou isométriques, qui sont placées selon un motif régulier. De cette façon, il n'y a aucun espace non couvert et les carreaux ou mosaïques ne se chevauchent pas..
Dans le cas où un seul type de mosaïque formé par un polygone régulier est utilisé, alors il y a un pavage régulier, mais si deux ou plusieurs types de polygones réguliers sont utilisés, alors c'est un tessellation semi-régulière.

Enfin, lorsque les polygones qui forment la tessellation ne sont pas réguliers, alors c'est un tessellation irrégulière.
Le type de pavage le plus courant est celui formé par des mosaïques rectangulaires et particulièrement carrées. Dans la figure 1, nous avons un bon exemple.
Index des articles
- 1 Histoire des pavages
- 2 pavages réguliers
- 2.1 Nomenclature
- 2.2 Exemple 1: pavage triangulaire
- 2.3 Exemple 2: pavage carré
- 2.4 Exemple 3: pavage hexagonal
- 3 pavages semi-réguliers
- 3.1 Exemple 4: tessellation tri-hexagonale
- 3.2 Exemple 5: pavage hexagonal émoussé
- 3.3 Exemple 6: pavage rhombi-tri-hexagonal
- 4 pavages irréguliers
- 4.1 Exemple 7
- 4.2 Exemple 8
- 4.3 Exemple 9
- 4.4 Exemple 10: tessellation du Caire
- 4.5 Exemple 11: tessellation Al-Andalus
- 4.6 Exemple 12: tessellation dans les jeux vidéo
- 5 Références
Histoire des pavages
Pendant des milliers d'années, la tessellation a été utilisée pour recouvrir les sols et les murs des palais et des temples de différentes cultures et religions..
Par exemple, la civilisation sumérienne qui a prospéré vers 3500 avant JC. au sud de la Mésopotamie, entre l'Euphrate et le Tigre, ils ont utilisé des pavages dans leur architecture.

Les pavages ont également suscité l'intérêt des mathématiciens de tous âges: à commencer par Archimède au IIIe siècle avant JC, puis Johannes Kepler en 1619, Camille Jordan en 1880, jusqu'à l'époque contemporaine avec Roger Penrose..
Penrose a créé une tessellation non périodique connue sous le nom de Tessellation de Penrose. ETcelles-ci ne sont que quelques noms de scientifiques qui ont beaucoup contribué à la tessellation.
Tessellations régulières
Les pavages réguliers sont réalisés avec un seul type de polygone régulier. En revanche, pour que la tessellation soit considérée comme régulière, chaque point de l'avion doit:
-Appartiennent à l'intérieur du polygone
-Ou au bord de deux polygones adjacents
-Enfin il peut appartenir au sommet commun d'au moins trois polygones.
Avec les restrictions ci-dessus, on peut montrer que seuls les triangles équilatéraux, les carrés et les hexagones peuvent former une tessellation régulière.
Nomenclature
Il existe une nomenclature pour désigner les pavages qui consiste à lister dans le sens des aiguilles d'une montre et séparés par un point, le nombre de côtés des polygones qui entourent chaque nœud (ou sommet) de la pavage, en commençant toujours par le polygone avec le plus petit nombre. côtés.
Cette nomenclature s'applique aux pavages réguliers et semi-réguliers.
Exemple 1: pavage triangulaire
La figure 3 montre un pavage triangulaire régulier. Il est à noter que chaque nœud de la tessellation triangulaire est le sommet commun de six triangles équilatéraux.
La façon de désigner ce type de pavage est 3.3.3.3.3.3, qui est également noté 36.

Exemple 2: pavage carré
La figure 4 montre un pavage régulier composé uniquement de carrés. Il convient de noter que chaque nœud de la tessellation est entouré de quatre carrés congruents. La notation appliquée à ce type de pavage carré est: 4.4.4.4 ou bien 44

Exemple 3: pavage hexagonal
Dans une tessellation hexagonale, chaque nœud est entouré de trois hexagones réguliers comme le montre la figure 5. La nomenclature pour une tessellation hexagonale régulière est 6.6.6 ou 6.3.

Tessellations semi-régulières
Les pavages semi-réguliers ou archimédiens se composent de deux ou plusieurs types de polygones réguliers. Chaque nœud est entouré des types de polygones qui composent la tessellation, toujours dans le même ordre, et la condition de bord est entièrement partagée avec le voisin..
Il existe huit pavages semi-réguliers:
- 3.6.3.6 (tessellation tri-hexagonale)
- 3.3.3.3.6 (tessellation hexagonale émoussée)
- 3.3.3.4.4 (pavage triangulaire allongé)
- 3.3.4.3.4 (pavage carré émoussé)
- 3.4.6.4 (pavage rhombi-tri-hexagonal)
- 4.8.8 (pavage carré tronqué)
- 3.12.12 (pavage hexagonal tronqué)
- 4.6.12 (tessellation tri-hexagonale tronquée)
Quelques exemples de pavages semi-réguliers sont présentés ci-dessous.
Exemple 4: pavage tri-hexagonal
C'est celui qui est composé de triangles équilatéraux et d'hexagones réguliers dans la structure 3.6.3.6, ce qui signifie qu'un nœud de la tessellation est entouré (jusqu'à la fin d'un tour) par un triangle, un hexagone, un triangle et un hexagone. La figure 6 montre une telle tessellation.

Exemple 5: pavage hexagonal émoussé
Comme la tessellation de l'exemple précédent, celle-ci est également constituée de triangles et d'hexagones, mais leur distribution autour d'un nœud est 3.3.3.3.6. La figure 7 illustre clairement ce type de pavage.

Exemple 6: pavage rhombi-tri-hexagonal
C'est un pavage composé de triangles, de carrés et d'hexagones, dans la configuration 3.4.6.4, qui est représentée sur la figure 8.
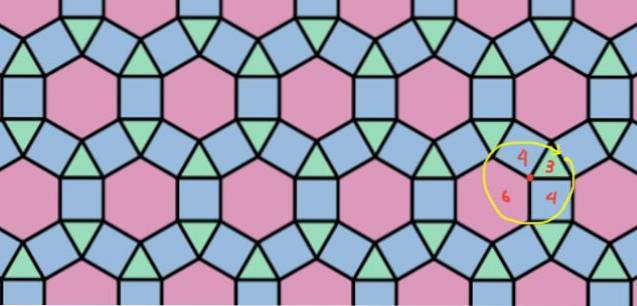
Tessellations irrégulières
Les pavages irréguliers sont ceux qui sont formés par des polygones irréguliers ou par des polygones réguliers mais qui ne remplissent pas le critère selon lequel un nœud est un sommet d'au moins trois polygones.
Exemple 7
La figure 9 montre un exemple de pavage irrégulier, dans lequel tous les polygones sont réguliers et congruents. Il est irrégulier car un nœud n'est pas un sommet commun d'au moins trois carrés et il y a aussi des carrés voisins qui ne partagent pas complètement une arête.
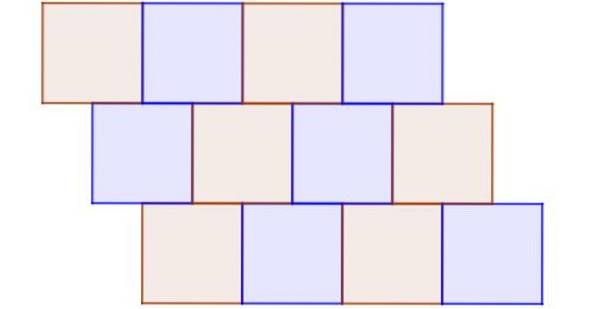
Exemple 8
Le parallélogramme dalle une surface plane, mais à moins qu'il ne s'agisse d'un carré, il ne peut pas former une tessellation régulière.

Exemple 9
Des hexagones non réguliers à symétrie centrale pavent une surface plane, comme le montre la figure suivante:

Exemple 10: pavage du Caire
C'est une tessellation très intéressante, composée de pentagones avec des côtés de longueur égale mais avec des angles inégaux, dont deux sont droits et les trois autres ont 120º chacun..
Son nom vient du fait que cette tessellation se trouve dans le trottoir de certaines rues du Caire en Egypte. La figure 12 montre la tessellation du Caire.

Exemple 11: tessellation Al-Andalus
La tessellation de certaines régions d'Andalousie et d'Afrique du Nord est caractérisée par la géométrie et l'épigraphie, en plus d'éléments ornementaux tels que la végétation..
La tessellation des palais comme celle de l'Alhambra était composée de carreaux constitués de pièces de céramique de nombreuses couleurs, aux formes multiples (sinon infinies) qui déchaînaient des motifs géométriques..

Exemple 12: tessellation dans les jeux vidéo
Aussi connu sous le nom de tesellation, c'est l'une des nouveautés les plus populaires dans les jeux vidéo. Il s'agit de la création de textures pour simuler la tessellation des différents scénarios qui apparaissent dans le simulateur.
C'est le reflet clair que ces revêtements continuent d'évoluer, traversant les frontières de la réalité..
Les références
- Profitez des maths. Tessellations. Récupéré de: gustolasmatematicas.com
- Rubiños. Tessellations a résolu des exemples. Récupéré de: matematicasn.blogspot.com
- Weisstein, Eric W. "Tessellation démirégulaire". Weisstein, Eric W, éd. MathWorld. Recherche Wolfram.
- Wikipédia. Tessellation. Récupéré de: es.wikipedia.com
- Wikipédia. Pavage régulier. Récupéré de: es.wikipedia.com



Personne n'a encore commenté ce post.